Pasiruošimas egzaminui internetu. Vieningo valstybinio egzamino simuliatorius anglų kalba

Instrukcijos

Pagal lygiašonės trapecijos savybę atkarpa n lygi pusei skirtumo tarp bazių x ir y. Todėl mažesnė trapecijos y bazė gali būti pavaizduota kaip skirtumas tarp didesnės bazės ir atkarpos n, padaugintas iš dviejų: y = x - 2*n.

Raskite nežinomą mažesnę atkarpą n. Norėdami tai padaryti, apskaičiuokite vieną iš rezultato pusių stačiakampis trikampis. Trikampį sudaro aukštis - h (koja), kraštinė - a (hipotenuzė) ir atkarpa - n (koja). Pagal Pitagoro teoremą nežinoma kojelė n² = a² - h². Pakaitalas skaitines reikšmes ir apskaičiuokite kojos n kvadratą. Paimkite gautos vertės kvadratinę šaknį - tai bus atkarpos n ilgis.

Pakeiskite šią reikšmę pirmoje lygtyje, kad apskaičiuotumėte y. Trapecijos plotas apskaičiuojamas pagal formulę S = ((x + y)*h)/2. Išreikškite nežinomą kintamąjį: y = 2*S/h – x.

Šaltiniai:

• lygiašonės trapecijos aukštis

Norint apibrėžti keturkampį, pavyzdžiui, trapeciją, turi būti apibrėžtos bent trys jo kraštinės. Todėl, pavyzdžiui, galime svarstyti problemą, kurioje pateikti įstrižainių ilgiai trapecijos, taip pat vienas iš šoninių vektorių.

Instrukcijos

Paveikslas iš probleminių sąlygų pateiktas 1.B šiuo atveju reikia manyti, kad nagrinėjamas yra ABCD, kuriame pateikti įstrižainių AC ir BD ilgiai, taip pat pusėje AB, pavaizduotas vektoriumi a(ax,ay). Priimti pradiniai duomenys leidžia rasti abu pagrindu trapecijos(ir viršuje, ir apačioje). IN konkretus pavyzdys pirmiausia bus rasta apatinė bazė AD.

Apsvarstykite trikampį ABD. Jos kraštinės AB ilgis lygus absoliučiai vektoriaus a reikšmei. Tegu |a|=sqrt((ax)^2+(ay)^2)=a, tada cosф =ax/sqrt(((ax)^2+(ay)^2), kaip krypties a kosinusą. Tegul turi pateiktą įstrižainę BD ilgio p, ir norimą AD ilgio X. Tada pagal kosinuso teoremą P^2=a^2+ x^2-2axcosф. Arba x^2-2axcosф+(a^2-p^2)=0.

Norėdami rasti viršūnę pagrindu BC (jo ilgis ieškant taip pat žymimas x), naudojamas modulis |a|=a, taip pat antroji įstrižainė BD=q ir kampo ABC kosinusas, kuris akivaizdžiai lygus (n-ph) .

Toliau svarstome trikampis ABC, prie kurios, kaip ir anksčiau, kyla kosinuso teorema ir taip. Atsižvelgiant į tai, kad cos(п-ф)=-cosф, remiantis AD sprendimu, galime naudoti šią formulę, pakeisdami p q:ВС=- a*ax|sqrt(((ax)^2+(ay) ^2) +sqrt((((a)^2)(ax^2))/(ax^2+ay^2))-a^2+q^2).

Tai yra kvadratas ir, atitinkamai, turi dvi šaknis. Taigi šiuo atveju belieka rinktis tik tas šaknis, kurios turi teigiama vertė, nes ilgis negali būti neigiamas.

Pavyzdys Įleisk trapecijos ABCD šoninė pusė AB nurodoma vektoriumi a(1, sqrt3), p=4, q=6. Rasti pagrindu trapecijos.Sprendimas. Naudodami aukščiau gautus algoritmus, galime parašyti: |a|=a=2, cosф=1/2. AD=1/2+sqrt(4/4 -4+16)=1/2 +sqrt(13)=(sqrt(13)+1)/2.BC=-1/2+sqrt(-3+36) )=(sqrt(33)-1)/2.

Video tema

Trapecija yra keturkampis, kurio dvi kraštinės yra lygiagrečios, o kitos dvi ne. Trapecijos aukštis yra atkarpa, statmena tarp dviejų lygiagrečių tiesių. Priklausomai nuo šaltinio duomenų, jį galima apskaičiuoti įvairiais būdais.

Jums reikės

• Šalių, pagrindų išmanymas, vidurio linija trapecija, taip pat, pasirinktinai, jos plotas ir (arba) perimetras.

Instrukcijos

Tarkime, kad yra trapecija su tais pačiais duomenimis, kaip ir 1 paveiksle. Nubrėžkime 2 aukščius, gausime , kuri turi 2 mažesnes kraštines pagal stačiakampių trikampių kojeles. Mažesnį ritinį pažymėkime x. Jis nustatomas padalijus ilgio skirtumą tarp didesnių ir mažesnių pagrindų. Tada pagal Pitagoro teoremą aukščio kvadratas lygi sumai hipotenuzės d ir kojos x kvadratai. Iš šios sumos išimame aukštį h. (2 pav.)

Video tema

Šaltiniai:

• kaip apskaičiuoti trapecijos aukštį

Matematinė figūra su keturiais kampais vadinama trapecija, jei jos priešingų kraštinių pora yra lygiagrečios, o kita pora ne. Lygiagrečios pusės vadinamos priežasčių trapecijos, kiti du yra šoniniai. Stačiakampyje trapecijos vienas iš šoninių kampų yra tiesus.

Instrukcijos

Užduotis 1. Raskite pagrindus BC ir AD trapecijos, jei žinomas ilgis AC = f; kraštinės ilgis CD = c ir kampas ADC = α Sprendimas: Apsvarstykite stačiakampį CED. Žinomi hipotenuzė c ir kampas tarp hipotenuzės ir kojos EDC. Raskite ilgius CE ir ED: naudodami kampo formulę CE = CD*sin(ADC); ED = CD*cos (ADC). Taigi: CE = c*sinα; ED=c*cosα.

Apsvarstykite stačiąjį trikampį ACE. Žinote hipotenuzę AC ir CE, raskite kraštinę AE pagal taisyklę: kojų kvadratų suma yra lygi hipotenuzės kvadratui. Taigi: AE(2) = AC(2) - CE(2) = f(2) - c*sinα. Apskaičiuokite kvadratinė šaknis iš dešinės lygybės pusės. Jūs radote viršutinį stačiakampį trapecijos.

Pagrindo AD ilgis yra dviejų atkarpų AE ir ED ilgių suma. AE = kvadratinė šaknis(f(2) - c*sinα); ED = c*cosα).Taigi: AD = kvadratinė šaknis(f(2) - c*sinα) + c*cosα.Jūs radote apatinį stačiakampio pagrindą trapecijos.

2 užduotis. Raskite stačiakampio pagrindus BC ir AD trapecijos, jei žinomas įstrižainės ilgis BD = f; kraštinės ilgis CD = c ir kampas ADC = α Sprendimas: Apsvarstykite stačiąjį trikampį CED. Raskite kraštinių CE ir ED ilgius: CE = CD*sin(ADC) = c*sinα; ED = CD*cos(ADC) = c*cosα.

Apsvarstykite stačiakampį ABCE. Pagal savybę AB = CE = c*sinα Apsvarstykite statųjį trikampį ABD. Pagal stačiojo trikampio savybę hipotenuzės kvadratas yra kojų kvadratų suma. Todėl AD(2) = BD(2) - AB(2) = f(2) - c*sinα Jūs radote apatinį stačiakampio pagrindą trapecijos AD = kvadratinė šaknis(f(2) - c*sinα).

Pagal stačiakampio taisyklę BC = AE = AD - ED = kvadratinė šaknis(f(2) - c*sinα) - c*cosα. Radote viršutinį stačiakampio pagrindą trapecijos.

Mažesnis trapecijos pagrindas yra viena iš lygiagrečių jos kraštinių, kurios ilgis yra minimalus. Šią vertę galima apskaičiuoti keliais būdais naudojant tam tikrus duomenis.

Jums reikės

• - skaičiuotuvas.

Instrukcijos

Jei žinomi du ilgiai – bazė ir vidurinė linija – naudokite trapecijos savybę, kad apskaičiuotumėte mažiausią bazę. Pagal ją trapecijos vidurio linija yra identiška pusei bazių sumos. Šiuo atveju mažiausias pagrindas bus lygus skirtumui tarp dvigubo vidurinės linijos ilgio ir šios figūros didžiojo pagrindo ilgio.

Jei žinomi tokie trapecijos parametrai kaip , aukštis, didžiojo pagrindo ilgis, tada pagal trapeciją apskaičiuokite mažiausią šios bazės pagrindą. Šiuo atveju galutinis rezultatas gaunamas iš skirtumo tarp dvigubo ploto ir aukščio koeficiento atėmus parametrą, pvz., trapecijos didžiojo pagrindo ilgį.

Apskaičiuokite kitos pusės šoninės pusės ilgį

Įvairių testų ir egzaminų medžiagoje jų labai dažnai randama trapecijos problemos, kurio sprendimui reikia žinoti jo savybes.

Sužinokime, kokių įdomių ir naudingų savybių turi trapecija sprendžiant uždavinius.

Ištyrus trapecijos vidurio linijos savybes, galima suformuluoti ir įrodyti atkarpos, jungiančios trapecijos įstrižainių vidurio taškus, savybė. Atkarpa, jungianti trapecijos įstrižainių vidurio taškus, yra lygi pusei pagrindų skirtumo.

MO – vidurinė linija trikampis ABC ir lygus 1/2ВС (1 pav.).

MQ yra trikampio ABD vidurinė linija ir lygi 1/2AD.

Tada OQ = MQ – MO, todėl OQ = 1/2AD – 1/2BC = 1/2 (AD – BC).

Sprendžiant daug problemų ant trapecijos, vienas iš pagrindinių metodų yra nubrėžti joje du aukščius.

Apsvarstykite šiuos dalykus užduotis.

Tegu BT yra lygiašonės trapecijos ABCD aukštis su bazėmis BC ir AD, kai BC = a, AD = b. Raskite atkarpų AT ir TD ilgius.

Sprendimas.

Išspręsti problemą nėra sunku (2 pav.), bet tai leidžia jums gauti lygiašonės trapecijos, nubrėžtos iš viršūnės, aukščio savybė bukas kampas : lygiašonės trapecijos aukštis, nubrėžtas iš buko kampo viršūnės, dalijasi didesnė bazėį du segmentus, iš kurių mažesnis lygus pusei bazių skirtumo, o didesnis – pusei bazių sumos.

Tiriant trapecijos savybes, reikia atkreipti dėmesį į tokią savybę kaip panašumas. Taigi, pavyzdžiui, trapecijos įstrižainės padalija ją į keturis trikampius, o šalia pagrindų esantys trikampiai yra panašūs, o trikampiai, esantys šalia kraštinių, yra vienodo dydžio. Šis teiginys gali būti vadinamas trikampių, į kuriuos trapecija padalinta iš įstrižainių, savybė. Be to, pirmąją teiginio dalį galima labai lengvai įrodyti trikampių, esančių dviem kampais, panašumo ženklu. Įrodykime antra pareiškimo dalis.

Trikampiai BOC ir COD turi bendrą aukštį (3 pav.), jei atkarpas BO ir OD imsime kaip jų pagrindus. Tada S BOC /S COD = BO/OD = k. Todėl S COD = 1/k · S BOC .

Panašiai trikampiai BOC ir AOB turi bendrą aukštį, jei jų pagrindus laikome atkarpas CO ir OA. Tada S BOC /S AOB = CO/OA = k ir S A O B = 1/k · S BOC .

Iš šių dviejų sakinių išplaukia, kad S COD = S A O B.

Neapsigyvenkime ties suformuluotu teiginiu, o raskime santykis tarp trikampių, į kuriuos trapecija padalinta įstrižainėmis, plotų. Norėdami tai padaryti, išspręskime šią problemą.

Tegul taškas O yra trapecijos ABCD įstrižainių susikirtimo taškas su pagrindais BC ir AD. Yra žinoma, kad trikampių BOC ir AOD plotai yra lygūs atitinkamai S 1 ir S 2. Raskite trapecijos plotą.

Kadangi S COD = S A O B, tai S ABC D = S 1 + S 2 + 2S COD.

Iš trikampių BOC ir AOD panašumo išplaukia, kad BO/OD = √(S₁/S 2).

Todėl S₁/S COD = BO/OD = √(S1/S 2), o tai reiškia, kad S COD = √(S 1 · S 2).

Tada S ABC D = S 1 + S 2 + 2√(S 1 · S 2) = (√S 1 + √S 2) 2.

Naudojant panašumą įrodyta, kad atkarpos, einančios per trapecijos, lygiagrečios pagrindams įstrižainių susikirtimo tašką, savybė.

Pasvarstykime užduotis:

Tegul taškas O yra trapecijos ABCD įstrižainių susikirtimo taškas su pagrindais BC ir AD. BC = a, AD = b. Raskite atkarpos PK, einančios per pagrindams lygiagrečių trapecijos įstrižainių susikirtimo tašką, ilgį. Kokias atkarpas PK dalija taškas O (4 pav.)?

Iš trikampių AOD ir BOC panašumo išplaukia, kad AO/OC = AD/BC = b/a.

Iš trikampių AOP ir ACB panašumo išplaukia, kad AO/AC = PO/BC = b/(a + b).

Taigi PO = BC b / (a ​​+ b) = ab / (a ​​+ b).

Panašiai iš trikampių DOK ir DBC panašumo išplaukia, kad OK = ab/(a + b).

Taigi PO = gerai ir PK = 2ab/(a + b).

Taigi, įrodyta savybė gali būti suformuluota taip: segmentas, lygiagrečiai pagrindams trapecija, einanti per įstrižainių susikirtimo tašką ir jungianti du taškus šonuose, dalinama per pusę įstrižainių susikirtimo taško. Jo ilgis yra trapecijos pagrindų harmoninis vidurkis.

Sekant keturių taškų savybė: trapecijoje toje pačioje tiesėje yra įstrižainių susikirtimo taškas, kraštinių tęsinio susikirtimo taškas, trapecijos pagrindų vidurio taškai.

Trikampiai BSC ir ASD yra panašūs (5 pav.) o kiekvienoje iš jų medianos ST ir SG viršūnės kampą S dalija į lygias dalis. Todėl taškai S, T ir G yra toje pačioje tiesėje.

Taip pat taškai T, O ir G yra toje pačioje tiesėje. Tai išplaukia iš trikampių BOC ir AOD panašumo.

Tai reiškia, kad visi keturi taškai S, T, O ir G yra toje pačioje tiesėje.

Taip pat galite rasti atkarpos, padalijančios trapeciją į dvi panašias, ilgį.

Jei trapecijos ALFD ir LBCF yra panašios (6 pav.), tada a/LF = LF/b.

Taigi LF = √(ab).

Taigi atkarpos, dalijančios trapeciją į dvi panašias trapecijas, ilgis yra lygus pagrindų ilgių geometriniam vidurkiui.

Įrodykime atkarpos, dalijančios trapeciją į dvi lygias sritis, savybė.

Tegul trapecijos plotas yra S (7 pav.). h 1 ir h 2 yra aukščio dalys, o x yra norimos atkarpos ilgis.

Tada S/2 = h 1 (a + x)/2 = h 2 (b + x)/2 ir

S = (h 1 + h 2) · (a + b)/2.

Sukurkime sistemą

(h 1 (a + x) = h 2 (b + x)
(h 1 · (a + x) = (h 1 + h 2) · (a + b)/2.

Sprendžiant šią sistemą, gauname x = √(1/2(a 2 + b 2)).

Taigi, atkarpos, dalijančios trapeciją į dvi lygias, ilgis lygus √((a 2 + b 2)/2)(vidutinis bazinio ilgio kvadratas).

Taigi trapecijos ABCD su bazėmis AD ir BC (BC = a, AD = b) įrodėme, kad atkarpa:

1) MN, jungiantis trapecijos šoninių kraštinių vidurio taškus, yra lygiagretus pagrindams ir lygus jų pusei (vidurkis aritmetiniai skaičiai a ir b);

2) PK, einantis per trapecijos įstrižainių susikirtimo tašką, lygiagrečią pagrindams, yra lygus
2ab/(a + b) (skaičių a ir b harmoninis vidurkis);

3) LF, kuris padalija trapeciją į dvi panašias trapecijas, ilgis lygus vidurkiui geometriniai skaičiai a ir b, √(ab);

4) EH, padalijant trapeciją į dvi lygias, ilgis yra √((a 2 + b 2)/2) (skaičių a ir b kvadrato vidurkis).

Įbrėžtos ir apribotos trapecijos ženklas ir savybė.

Įbrėžtos trapecijos savybės: trapecija gali būti įbrėžta į apskritimą tada ir tik tada, kai ji yra lygiašonė.

Aprašytos trapecijos savybės. Trapecija gali būti aprašyta aplink apskritimą tada ir tik tada, kai pagrindų ilgių suma yra lygi kraštinių ilgių sumai.

Naudingos to, kad į trapeciją įrašytas apskritimas, pasekmės:

1. Apribotos trapecijos aukštis lygus dviem įbrėžto apskritimo spinduliams.

2. Aprašytos trapecijos kraštinė matoma iš įbrėžto apskritimo centro stačiu kampu.

Pirmasis yra akivaizdus. Norint įrodyti antrąją išvadą, būtina nustatyti, kad kampas COD yra teisingas, o tai taip pat nėra sunku. Tačiau žinant šią pasekmę, sprendžiant problemas galima naudoti stačiąjį trikampį.

Patikslinkime lygiašonės trapecijos pasekmės:

Lygiašonės trapecijos aukštis yra vidutinis geometriniai pagrindai trapecijos
h = 2r = √(ab).

Apsvarstytos savybės leis giliau suprasti trapeciją ir užtikrinti sėkmę sprendžiant problemas naudojant jos savybes.

Vis dar turite klausimų? Nežinote, kaip išspręsti trapecijos problemas?
Norėdami gauti pagalbą iš dėstytojo -.
Pirma pamoka nemokama!

blog.site, kopijuojant visą medžiagą ar jos dalį, būtina nuoroda į pirminį šaltinį.

Apribotas apskritimas ir trapecija. Sveiki! Jums yra dar vienas leidinys, kuriame apžvelgsime problemas, susijusias su trapecijomis. Užduotys yra matematikos egzamino dalis. Čia jie sujungiami į grupę, pateikiama ne tik viena trapecija, o kūnų derinys – trapecija ir apskritimas. Dauguma šių problemų sprendžiamos žodžiu. Tačiau yra ir kai kurių, kuriuos reikia spręsti. ypatingas dėmesys, pavyzdžiui, 27926 užduotis.

Kokią teoriją reikia atsiminti? Tai:

Galima peržiūrėti problemas, susijusias su trapecijomis, kurios yra tinklaraštyje Čia.

27924. Aplink trapeciją aprašytas apskritimas. Trapecijos perimetras lygus 22, vidurio linija 5. Raskite trapecijos kraštinę.

Atkreipkite dėmesį, kad apskritimą galima apibūdinti tik aplink lygiašonę trapeciją. Mums duota vidurinė linija, o tai reiškia, kad galime nustatyti bazių sumą, tai yra:

Tai reiškia, kad kraštinių suma bus lygi 22–10=12 (perimetras atėmus pagrindą). Kadangi lygiašonės trapecijos kraštinės yra lygios, viena kraštinė bus lygi šešioms.

27925. Lygiašonės trapecijos šoninė kraštinė lygi jos mažesnė bazė, kampas prie pagrindo lygus 60 0, didesnis pagrindas – 12. Raskite šios trapecijos apibrėžtojo apskritimo spindulį.

Jei išsprendėte uždavinius su apskritimu ir jame įrašytu šešiakampiu, tuomet iš karto išgirsite atsakymą – spindulys yra 6. Kodėl?

Žiūrėkite: lygiašonė trapecija, kurios pagrindo kampas lygus 60 0 ir lygios pusės AD, DC ir CB reiškia pusę įprasto šešiakampio:

Tokiame šešiakampyje atkarpa jungiasi priešingos viršūnės eina per apskritimo centrą. *Šešiakampio centras ir apskritimo centras sutampa, daugiau detalių

Tai yra, didesnis šios trapecijos pagrindas sutampa su apibrėžto apskritimo skersmeniu. Taigi spindulys yra šeši.

*Žinoma, galime svarstyti trikampių ADO, DOC ir OCB lygybę. Įrodykite, kad jie yra lygiakraščiai. Toliau daryti išvadą, kad kampas AOB lygus 180 0, o taškas O yra vienodu atstumu nuo viršūnių A, D, C ir B, todėl AO=OB=12/2=6.

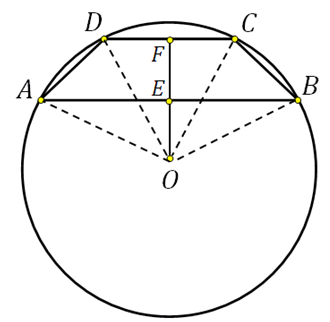
27926. Lygiašonės trapecijos pagrindai yra 8 ir 6. Apriboto apskritimo spindulys lygus 5. Raskite trapecijos aukštį.

Atkreipkite dėmesį, kad apibrėžto apskritimo centras yra ant simetrijos ašies, o jei sudarysime trapecijos, einančios per šį centrą, aukštį, tada, kai ji susikirs su bazėmis, ji padalys juos per pusę. Parodykime tai eskize ir taip pat sujunkite centrą su viršūnėmis:

Atkarpa EF yra trapecijos aukštis, turime jį rasti.

Stačiakampiame trikampyje OFC žinome hipotenuzą (tai yra apskritimo spindulys), FC=3 (kadangi DF=FC). Naudodami Pitagoro teoremą galime apskaičiuoti OF:

Stačiakampiame trikampyje OEB žinome hipotenuzą (tai yra apskritimo spindulys), EB=4 (kadangi AE=EB). Naudodami Pitagoro teoremą galime apskaičiuoti OE:

Taigi EF=FO+OE=4+3=7.

Dabar svarbus niuansas!

Šioje užduotyje paveikslėlyje aiškiai matyti, kad pagrindai yra išilgai skirtingos pusės nuo apskritimo centro, todėl problema išspręsta taip.

O kas, jei sąlygose nebūtų eskizo?

Tada problema turėtų du atsakymus. Kodėl? Atidžiai pažiūrėkite – dvi trapecijos su duotais pagrindais gali būti įrašytos bet kuriame apskritime:

*Tai yra, atsižvelgiant į trapecijos pagrindus ir apskritimo spindulį, yra dvi trapecijos.

O „antrojo varianto“ sprendimas bus toks.

Naudodami Pitagoro teoremą apskaičiuojame OF:

Taip pat apskaičiuokime OE:

Taigi EF=FO–OE=4–3=1.

Žinoma, užduotyje su trumpu atsakymu apie vieningą valstybinį egzaminą negali būti dviejų atsakymų, o be eskizo panašios problemos nebus pateikta. Todėl atkreipkite ypatingą dėmesį į eskizą! Būtent: kaip yra trapecijos pagrindai. Tačiau užduotyse su išsamiu atsakymu tai buvo ankstesniais metais (su šiek tiek sudėtingesne sąlyga). Tie, kurie svarstė tik vieną trapecijos vietos variantą, dėl šios užduoties prarado tašką.

27937. Aplink apskritimą, kurio perimetras lygus 40, apibrėžiama trapecija. Raskite jos vidurio liniją.

Čia iš karto turėtume prisiminti apie apskritimą apibrėžto keturkampio savybę:

Sumos priešingos pusės bet kuris apie apskritimą apibrėžtas keturkampis yra lygus.

Norint jaustis užtikrintai ir sėkmingai spręsti uždavinius geometrijos pamokose, neužtenka išmokti formulių. Pirmiausia juos reikia suprasti. Bijoti, o juo labiau nekęsti formulių – neproduktyvu. Šiame straipsnyje prieinama kalba bus analizuojamas įvairių būdų Trapecijos ploto radimas. Norėdami geriau suprasti atitinkamas taisykles ir teoremas, atkreipsime dėmesį į jo savybes. Tai padės suprasti, kaip veikia taisyklės ir kokiais atvejais reikėtų taikyti tam tikras formules.

Trapecijos apibrėžimas

Kokia tai apskritai figūra? Trapecija yra daugiakampis su keturiais kampais ir dviem lygiagrečiomis kraštinėmis. Kitos dvi trapecijos pusės gali būti pasvirusios skirtingais kampais. Ji lygiagrečios pusės yra vadinami bazėmis, o nelygiagrečioms pusėms naudojamas pavadinimas „šonai“ arba „klubai“. Tokie skaičiai yra gana dažni kasdienybė. Trapecijos kontūrai matomi drabužių, interjero daiktų, baldų, indų ir daugelio kitų siluetuose. Atsiranda trapecija skirtingų tipų: skalinė, lygiakraštė ir stačiakampė. Toliau straipsnyje mes išsamiau išnagrinėsime jų tipus ir savybes.

Trapecijos savybės

Trumpai pakalbėkime apie šio paveikslo savybes. Kampų, esančių šalia bet kurios kraštinės, suma visada yra 180°. Reikėtų pažymėti, kad visi trapecijos kampai sudaro 360°. Trapecija turi vidurio linijos sąvoką. Jei kraštinių vidurio taškus sujungsite su segmentu, tai bus vidurinė linija. Jis žymimas m. Vidurinė linija turi svarbios savybės: jis visada yra lygiagretus pagrindams (atsimename, kad pagrindai taip pat lygiagrečiai vienas kitam) ir lygus jų pusei:

Šį apibrėžimą reikia išmokti ir suprasti, nes tai yra raktas į daugelio problemų sprendimą!

Naudodami trapeciją, visada galite nuleisti aukštį iki pagrindo. Aukštis yra statmenas, dažnai žymimas simboliu h, brėžiamas iš bet kurio vieno pagrindo taško į kitą bazę arba jos tęsinį. Vidurinė linija ir aukštis padės rasti trapecijos plotą. Panašios užduotys yra labiausiai paplitę mokyklos kursas geometrija ir reguliariai pasirodo tarp kontrolinių ir egzaminų darbų.

Paprasčiausios trapecijos ploto formulės

Pažvelkime į du populiariausius ir paprastos formulės, kurio pagalba randamas trapecijos plotas. Pakanka aukštį padauginti iš pusės pagrindų sumos, kad lengvai rastumėte tai, ko ieškote:

S = h*(a + b)/2.

Šioje formulėje a, b žymi trapecijos pagrindus, h – aukštį. Kad būtų lengviau suvokti, šiame straipsnyje daugybos ženklai formulėse žymimi simboliu (*), nors oficialiose žinynuose daugybos ženklas dažniausiai praleidžiamas.

Pažiūrėkime į pavyzdį.

Pateikta: trapecija su dviem pagrindais, lygiais 10 ir 14 cm, aukštis yra 7 cm. Koks yra trapecijos plotas?

Pažvelkime į šios problemos sprendimą. Naudojant šią formulę, pirmiausia reikia rasti bazių pusę: (10+14)/2 = 12. Taigi, pusė sumos lygi 12 cm. Dabar pusę sumos padauginame iš aukščio: 12*7 = 84. Tai, ko ieškome, yra rasta. Atsakymas: Trapecijos plotas yra 84 kvadratiniai metrai. cm.

Antra garsioji formulė teigia: trapecijos plotas lygus vidurio linijos ir trapecijos aukščio sandaugai. Tai yra, tai iš tikrųjų išplaukia iš ankstesnės vidurinės linijos sampratos: S=m*h.

Įstrižainių naudojimas skaičiavimams

Kitas būdas rasti trapecijos plotą iš tikrųjų nėra toks sudėtingas. Jis yra prijungtas prie jo įstrižainių. Naudodami šią formulę, norėdami rasti plotą, turite padauginti jo įstrižainių pusgaminį (d 1 d 2) iš kampo tarp jų sinuso:

S = ½ d 1 d 2 sin a.

Panagrinėkime problemą, kuri parodo šio metodo taikymą. Duota: trapecija, kurios įstrižainių ilgis atitinkamai lygus 8 ir 13 cm Kampas a tarp įstrižainių yra 30°. Raskite trapecijos plotą.

Sprendimas. Naudojant aukščiau pateiktą formulę, lengva apskaičiuoti, ko reikia. Kaip žinote, nuodėmė 30° yra 0,5. Todėl S = 8*13*0,5=52. Atsakymas: plotas 52 kvadratiniai metrai. cm.

Lygiašonės trapecijos ploto radimas

Trapecija gali būti lygiašonė. Jo kraštinės vienodos, o kampai prie pagrindų lygūs, tai puikiai iliustruoja paveikslas. Lygiašonė trapecija turi tas pačias savybes kaip ir įprastas, be to, nemažai specialių. Aplink lygiašonę trapeciją galima apibrėžti apskritimą, o joje – apskritimą.

Kokie yra tokios figūros ploto apskaičiavimo metodai? Toliau pateiktam metodui reikės daug skaičiavimų. Norėdami jį naudoti, turite žinoti kampo ties trapecijos pagrindu sinuso (sin) ir kosinuso (cos) reikšmes. Jų skaičiavimams reikia arba Bradis lentelių, arba inžinerinis skaičiuotuvas. Štai formulė:

S = c*nuodėmė a*(a - c* cos a),

Kur Su- šoninės šlaunies, a- kampas prie apatinio pagrindo.

Lygiakraščio trapecijos įstrižainės yra vienodo ilgio. Taip pat yra priešingai: jei trapecijos įstrižainės yra lygios, tada ji yra lygiašonė. Iš čia sekančią formulę, kuris padeda rasti trapecijos plotą - įstrižainių kvadrato ir kampo tarp jų sinuso pusinės sandaugos: S = ½ d 2 sin a.

Stačiakampės trapecijos ploto radimas

Žinomas ypatingas atvejis stačiakampė trapecija. Tai trapecija, kurios viena pusė (jos šlaunys) stačiu kampu ribojasi su pagrindais. Jis turi įprastos trapecijos savybių. Be to, ji turi labai įdomi savybė. Tokios trapecijos įstrižainių kvadratų skirtumas lygus jos pagrindų kvadratų skirtumui. Tam naudojami visi anksčiau aprašyti ploto apskaičiavimo metodai.

Mes naudojame išradingumą

Yra vienas triukas, kuris gali padėti, jei pamiršite konkrečias formules. Pažiūrėkime atidžiau, kas yra trapecija. Jei mintyse suskirstysime jį į dalis, gausime pažįstamas ir suprantamas geometrines figūras: kvadratą arba stačiakampį ir trikampį (vieną ar du). Jei trapecijos aukštis ir kraštinės yra žinomi, galite naudoti trikampio ir stačiakampio ploto formules ir sudėti visas gautas reikšmes.

Pavaizduokime tai sekantį pavyzdį. Dana stačiakampė trapecija. Kampas C = 45°, kampai A, D yra 90°. Viršutinis trapecijos pagrindas yra 20 cm, aukštis - 16 cm. Reikia apskaičiuoti figūros plotą.

Ši figūra akivaizdžiai susideda iš stačiakampio (jei du kampai lygūs 90°) ir trikampio. Kadangi trapecija yra stačiakampė, jos aukštis lygus jos kraštinei, tai yra 16 cm. Turime stačiakampį, kurio kraštinės yra atitinkamai 20 ir 16 cm. Dabar apsvarstykite trikampį, kurio kampas yra 45 °. Žinome, kad viena jo kraštinė yra 16 cm. Kadangi ši kraštinė yra ir trapecijos aukštis (ir žinome, kad aukštis nusileidžia stačiu kampu), todėl antrasis trikampio kampas yra 90°. Taigi likęs trikampio kampas yra 45°. Dėl to gauname stačiakampį lygiašonis trikampis, kurio abi pusės yra vienodos. Tai reiškia, kad kita trikampio pusė yra lygi aukščiui, tai yra 16 cm. Belieka apskaičiuoti trikampio ir stačiakampio plotą ir pridėti gautas vertes.

Stačiakampio plotas lygus pusei jo kojų sandaugos: S = (16*16)/2 = 128. Stačiakampio plotas lygus jo pločio ir ilgio sandaugai: S = 20*16 = 320. Radome reikiamą: trapecijos plotas S = 128 + 320 = 448 kv. žr. Galite lengvai patikrinti save naudodami aukščiau pateiktas formules, atsakymas bus identiškas.

Mes naudojame Pick formulę

S = M/2 + N - 1,

šioje formulėje M yra mazgų skaičius, t.y. figūros linijų susikirtimo su langelio linijomis ties trapecijos ribomis (paveiksle oranžiniai taškai), N – mazgų skaičius figūros viduje (mėlyni taškai). Patogiausia jį naudoti ieškant ploto netaisyklingas daugiakampis. Tačiau kuo didesnis naudojamų technikų arsenalas, tuo mažiau klaidų ir geresni rezultatai.

Žinoma, pateikta informacija neišsemia trapecijos tipų ir savybių, taip pat jos ploto nustatymo būdų. Šiame straipsnyje apžvelgiamos svarbiausios jo savybės. Sprendžiant geometrinius uždavinius, svarbu veikti palaipsniui, pradėti nuo lengvų formulių ir uždavinių, nuosekliai įtvirtinti savo supratimą ir pereiti į kitą sudėtingumo lygį.

Surinktos dažniausiai pasitaikančios formulės padės mokiniams naršyti įvairiais būdais apskaičiuoti trapecijos plotą ir geriau pasiruošti testams bei bandymaišia tema.