Bir fonksiyonun sınırlılık kavramını kullanarak denklemi çözün. İsteğe bağlı ders “Sınırlı fonksiyonların özelliğinin uygulanması

İsteğe bağlı aktivite"Sınırlı fonksiyonların özelliğinin uygulanması"

Denklemler ve eşitsizliklerle ilgili materyaller okul matematik dersinin önemli bir bölümünü oluşturur, ancak dersin zaman çerçevesi tüm konuları dikkate almamıza izin vermez.

Ek olarak, temel okul için devlet standardı tarafından belirlenen zorunlu minimum matematik öğretimi içeriği belirlenir. Eğitim materyali zorunlu değerlendirme için, ancak zorunlu ustalık için değil (örneğin, denklemleri ve eşitsizlikleri çözmek için standart olmayan yöntemler, denklemleri ve eşitsizlikleri bir parametreyle çözme yöntemleri vb.).

Denklem ve eşitsizlik kavramlarıyla ilgili materyalin önemi ve genişliği nedeniyle, bunların modern yöntemler matematik içerik-metodolojik bir çizgi halinde düzenlenmiştir - bir denklemler ve eşitsizlikler çizgisi. Bu hattın konuşlandırılması için üç ana yön vardır. okul kursu matematik.

Denklem ve eşitsizlik çizgilerinin uygulanan yönü esas olarak çalışırken ortaya çıkar cebirsel yöntemçözümler kelime problemleri. Denklemler ve eşitsizlikler ana kısımdır matematiksel araçlar, sözlü problemlerin çözümünde kullanılır.

Teorik ve matematiksel yönelim iki açıdan ortaya çıkar: en önemli denklem sınıflarının, eşitsizliklerin ve bunların sistemlerinin incelenmesinde ve bir bütün olarak doğruya ilişkin genelleştirilmiş kavram ve yöntemlerin incelenmesinde.

Denklemler ve eşitsizlikler doğrusu da fonksiyonel doğru ile yakından ilişkilidir. Bir yanda denklemler ve eşitsizlikler doğrultusunda geliştirilen yöntemlerin fonksiyonların incelenmesine uygulanması var. Öte yandan, fonksiyonel doğrunun hem denklemler ve eşitsizlikler doğrusu içeriği hem de çalışma tarzı üzerinde önemli bir etkisi vardır. Özellikle fonksiyonel gösterimler, denklemlerin ve eşitsizliklerin çözümüne ve incelenmesine grafiksel netlik kazandırmak için temel oluşturur.

Mordkovich editörlüğünde çalıştığımız cebir dersinde öncelikli olarak fonksiyonel-grafik doğrusu seçilmiştir. Tüm materyaller katı bir şemaya göre inşa edilmiştir: fonksiyon-denklemler-dönüşümler.

Birleşik Devlet Sınavında sıklıkla fonksiyonların özellikleri kullanılarak çözülebilecek görevler vardır. Bu nedenle bu materyalin seçmeli derslere dahil edilmesi tavsiye edilir. Ama yine de bu görevlerin bazılarını 9. sınıftan itibaren derslerde ele almayı tercih ediyorum.

Denklemleri ve eşitsizlikleri çözerken fonksiyonların özelliklerini uygulamak

Sınırlılık özelliğini kullanma.

Bir işlevin kapsamını kullanma.

Denklemleri ve eşitsizlikleri çözmek için fonksiyonların monotonluğunu kullanmak.

Bir fonksiyonun değişim bölgesi kavramının kullanılması.

- Fonksiyonların çift ve tek ve periyodiklik özelliklerini kullanma.

SLAYT 2.

Sunumum, denklemde yer alan fonksiyonların sınırlılık özelliğine (eşitsizlik) dayanarak denklemleri ve eşitsizlikleri çözmek için standart olmayan yöntemlerden yalnızca birine adanmıştır. Önerdiğim problemler, öğrencileri Birleşik Devlet Sınavına hazırlamak için ayrılan derslerde (üç veya dört ders) değerlendirilebilir veya ders başına bir veya iki problem kullanılabilir ve bu materyal aynı zamanda seçmeli bir derste de kullanılabilir (veya seçmeli ders dersinde).

Zaten 9. sınıfta sınırlama özelliğini incelerken bu özelliğin önemine ve onu bilimde kullanma olasılığına dikkat çekmiştim.

Bir fonksiyonun en küçük ve en büyük değerini bulma;

Fonksiyon değerleri kümesini bulma.

SLAYT3.

Bazı görevlerin çözümleri dikkate alınır. Öncelikle temel tanımların tekrarlanması gerekmektedir. SLAYT 4.

5-9 arasındaki slaytlar, bir fonksiyonun en küçük veya en büyük değerlerini bulmaya yönelik görevleri inceliyor.

SLAYT 10.

Fonksiyonların sınırlılık özelliğinin denklem ve eşitsizliklerin çözümüne uygulanması.

1. ANA YÖNTEM (DEĞERLENDİRME YÖNTEMİ)

Majorant yönteminin ana fikri şu şekildedir:

Bir denklemimiz olsun ve böyle bir sayı var M bu herkes için X https://pandia.ru/text/78/376/images/image003_26.gif" width="160" height="23"> tanım alanından. O zaman denklem https://pandia sistemine eşdeğerdir. .ru/text/78 /376/images/image005_16.gif" width = "96" height = "35 src = ">.

Çözüm. Denklemin her iki tarafını da tahmin edelim.

Tüm değerler için X https://pandia.ru/text/78/376/images/image007_10.gif" width = "188" height = "59 src = "> eşitsizlikleri doğrudur.

Ortaya çıkan sistemin hiçbir çözümü yok çünkü https://pandia.ru/text/78/376/images/image009_6.gif" width="20" height="20">

Örnek 1.2 ..gif" genişlik = "157" yükseklik = "20">.gif" genişlik = "75" yükseklik = "51 src = ">.

Sistemin ilk denkleminin çözümü https://pandia.ru/text/78/376/images/image014_3.gif" width="201" height=48 src=> değerleridir.

Buradan, sistem çözümü.

Cevap: .

Örnek 1.3. Eşitsizliği çözün https://pandia.ru/text/78/376/images/image016_0.gif" width="56" height="19">.gif" width="84" height="21">.gif" genişlik = "156 yükseklik = 61" yükseklik = "61">.

Ters değiştirme: X + 1 = 0 .

Cevap: - 1.

Örnek 1.4. Tüm parametre değerlerini bulun A, her biri için denklemin çözümleri vardır. Bu çözümleri bulun.

Çözüm.

Denklemi formda yeniden yazalım. Tüm değerler için X ifade bu nedenle https://pandia.ru/text/78/376/images/image026_0.gif" width = "87" height = "19 src = "> ve ..gif" width = "405" yükseklik = "91">

Cevap: https://pandia.ru/text/78/376/images/image031_0.gif" genişlik = "51" yükseklik = "41 src = ">

2. “KENARDA BULUŞMA”

Ana yöntemin bir varyasyonu problemlerdir (“ kenarda buluşma") bir denklemin veya eşitsizliğin sol ve sağ taraflarındaki değer kümelerinin benzersiz olduğu ortak nokta Bu, bir parça için en büyük, diğer parça için en küçük değerdir.

Bu tür sorunları çözmeye nasıl başlanır? Her şeyden önce - getir verilen denklemler veya daha fazla eşitsizlik basit görünüm: çarpanlara ayırarak, modüllerden, logaritmalardan vb. kurtularak. Daha sonra görevi dikkatlice tekrar okumanız, çizmeye çalışmanız gerekir. grafik görüntü görevin içerdiği işlevler.

Örnek 2.1. Denklemi çözün.

Çözüm. Denklemin kökünü tahmin etmek kolaydır; X= 1. Ancak monotonluk hususlarından dolayı benzersizliğini kanıtlamak mümkün değildir çünkü denklemin ne sol ne de sağ tarafı monoton fonksiyonlar değildir. Burada başka bir fikir kullanılmış..gif" width="191" height="51">. Ortaya çıkan denklemin sağ tarafındaki en büyük değer 1'dir ve noktada alınır. X= 1..gif" width = "185" yükseklik = "52 src = ">). Bu nedenle Sol Taraf ulaşır X= en küçük değerinin 1'i ve bu da 1'e eşittir. Sonuç: Eşitlik ancak ve ancak her iki tarafın da aynı anda 1'e eşit olması durumunda sağlanır, yani. X = 1.

Örnek 2.2. Denklemi çözün.

1 yol.

Çözüm: Denklemin sol tarafının birliği aşmadığına dikkat edin. sağ kısım birden az değil. Buradan, orijinal denklem ancak her iki tarafı da bire eşitse çözümü vardır. Bu ancak ile mümkündür.

Cevap: .

Yöntem 2. Bu denklem grafiksel olarak çözülebilir. Bunu yapmak için, denklemin sağ ve sol taraflarının grafiklerini tek bir koordinat sisteminde, yani bir fonksiyonun grafiğini ve bir fonksiyonun grafiğini oluşturalım https://pandia.ru/text/78/376/images /image008_7.gif" genişlik = "37" yükseklik = "19">.

Cevap: .

Örnek 2.3. Denklemi çözün https://pandia.ru/text/78/376/images/image042_0.gif" width="301" height="35 src=">

O verilen denklem yalnızca sistem çalışıyorsa yürütülür . Sistemin ilk denkleminin tek kökü vardır X= 1, ancak bu kök ikinci denklemi sağlamaz. Bu nedenle sistemin çözümü yoktur.

Cevap: Æ

Örnek 2.4. Https://pandia.ru/text/78/376/images/image045_0.gif" width="105" height="21"> denklemini çözün, ardından denklemin sol tarafı 2'ye kadar bir değer alır. .gif" width = "137" height = "53">..gif" width = "217" height = "24">'in bir çözümü var.

Çözüm.

Cevap:

Örnek 2.6. Tüm parametre değerlerini bulun A bunun için denklem

Konu: Sınırlı işlevleri kullanma yöntemleri.
Hayat, içindekiler sayesinde güzel matematik yapabilirsin. (Leonard Euler)Hedefler: diğer alanlarda başarıyla uygulanabilecek yeni, alışılmadık düşüncenin geliştirilmesi insan aktivitesi(sibernetik, Bilgisayar Mühendisliği, ekonomi, radyofizik, kimya vb.).
Görevler: - görevlerin nesnel ve öznel zorluğunun değerlendirilmesi ve bu görevlerin sınavda makul seçimi konusunda eğitim;

Alışılmadık ve sıra dışı akıl yürütmelerden oluşan bir “kumbara” yaratmak.

Dersler sırasında:

Organizasyon an. Öğrenciler, Birleşik Devlet Sınavı ödevlerinin A ve B bölümlerini tamamlayarak ve alınan cevaplara göre konuyu azalan sırayla çözerek dersin konusunu oluştururlar. (-2'den 10'a kadar numaralandırılmış 12 kartı sözde kelime olarak şifreleyin) (Ek 1 ve 2)

sınırlamalar

Ek 1.
Bu görevleri çözün ve cevapları azalan sıraya göre düzenleyin, dersimizin konusunu cevaplara göre toplayın.

y=3x 2 -7x+7 fonksiyonunun grafiğindeki teğet açının tanjantının -1'e eşit olduğu noktanın apsisini bulun.

Ek 2.
9 2 0 7Türev kullanarak fonksiyonların incelenmesi. 10 5 1 -1Sınırlı işlevleri kullanma yöntemi. 4 -2 8 12Eşitsizlikleri grafiksel olarak çözme.
3 11 6Çözümler fonksiyonel denklemler.
Çalışmak

Biri etkili yöntemler Denklemleri veya eşitsizlikleri çözme, sınırlı fonksiyonların kullanımına dayanan bir yöntemdir. En ünlüsüne sınırlı işlevlerörneğin bazı trigonometrik bilgileri içerir; tersi trigonometrik fonksiyonlar; Modül, derece, çift dereceli kök ve diğerlerini içeren fonksiyonlar.

En yaygın eşitsizlikler şunlardır:

│f(x) │≥ 0, -1 ≤ sinx ≤ 1, -1 ≤ cosx ≤ 1, -

-

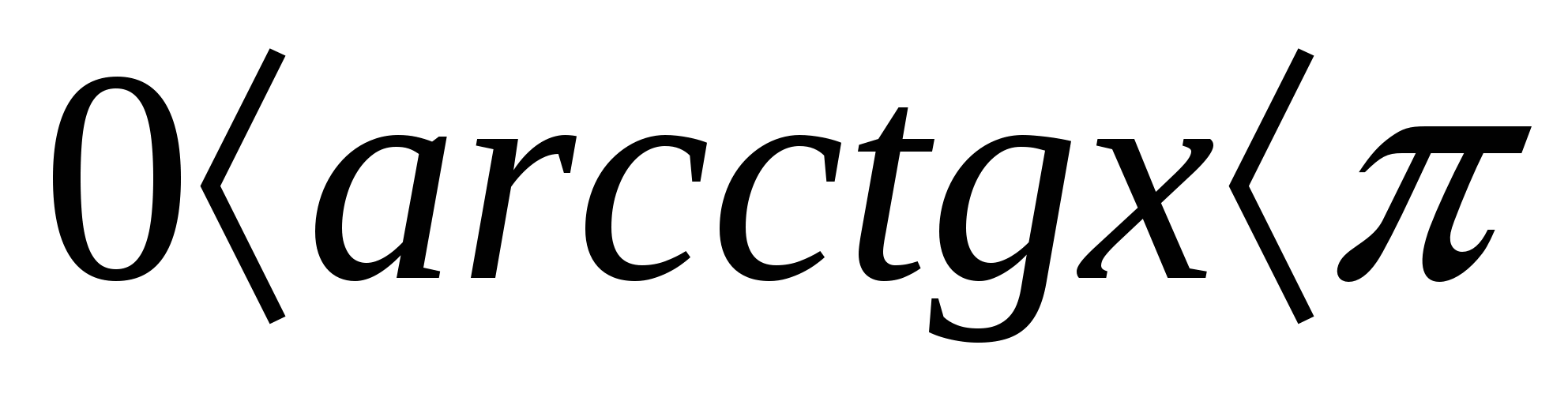, A f ( x ) >0, (f(x) ± g(x)) 2 n ≥ 0,
, A+ ≥ 2, B+ ≤ -2 Ve bircok digerleri. Burada N -doğal sayı, h(x) ≥ 0, A>0, B 0.

Yukarıda verilen en basit eşitsizliklere ek olarak daha karmaşık eşitsizlikler de vardır. trigonometrik eşitsizlikler -,

,

ve formun modülleri ile eşitsizlikler
.

Örnek 1.Denklemi çözün:

Çözüm: Denklemin sağ tarafında tam bir kare seçelim, yani. . Şunu takip ediyor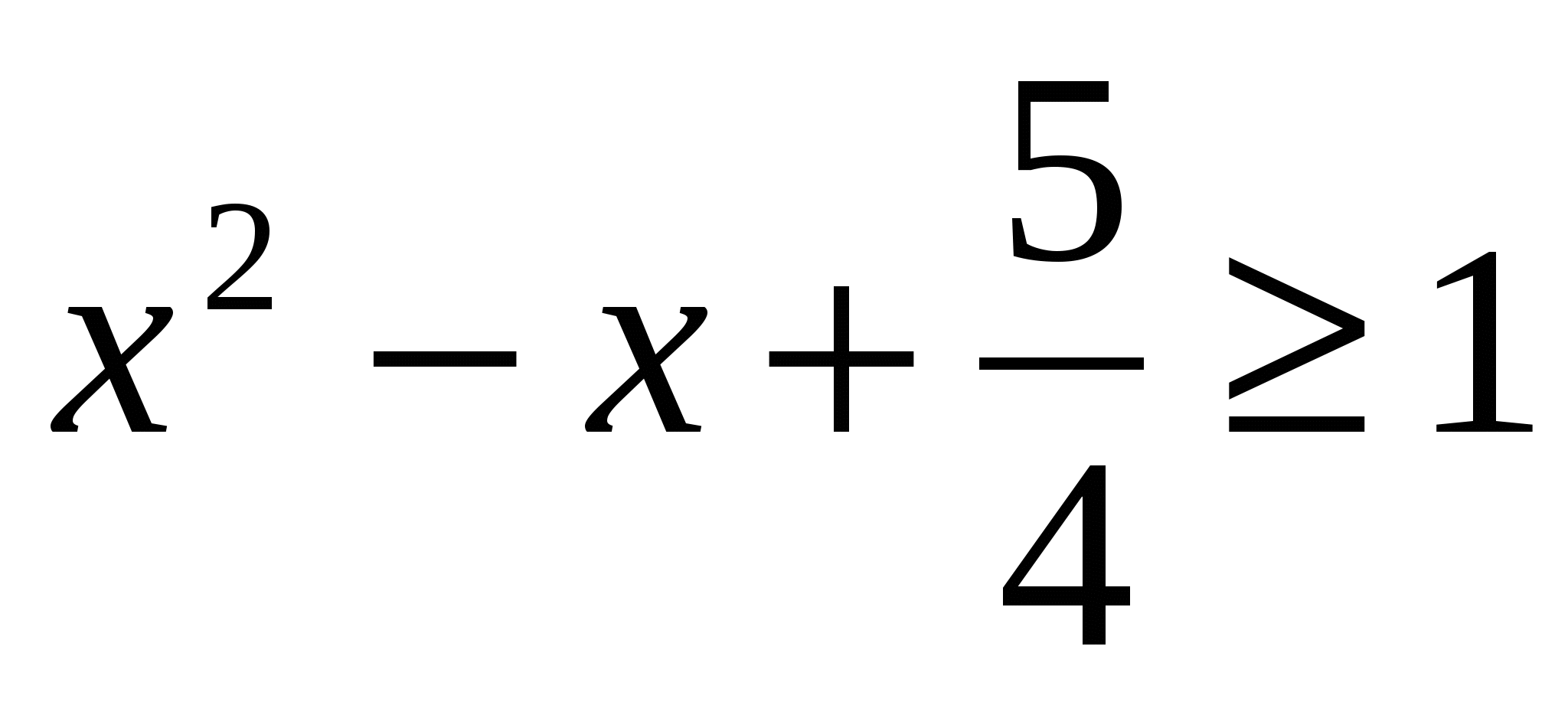
. Bu durumda olduğundan sinπ x ≤ 1, sonra bir denklem sistemi elde ederiz

Sistemin ikinci denklemini çözerek x= elde ederiz. İlk denklemi değiştirerek, x'in bulunan değerinin sistemin bir çözümü olduğundan ve dolayısıyla orijinal denklemin bir çözümü olduğundan emin oluruz.

Cevap: x=.

Örnek 2.Denklemi çözün:

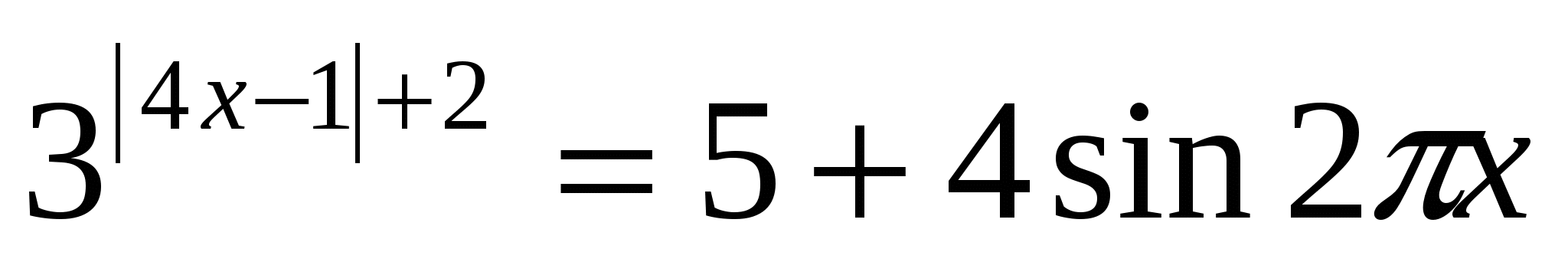
Çözüm: Çünkü Ancak sin2 π x ≤ 1. Dolayısıyla 5+4 sin2 π x ≤ 9. Böylece bir denklem sistemi elde ederiz:

Buradan bir denklem sistemi elde ederiz
, ilk denklemden x='yi buluyoruz. Bunu sistemin ikinci denkleminde yerine koyalım ve x ='nin sistemin bir çözümü olduğundan ve dolayısıyla orijinal denklemin bir çözümü olduğundan emin olalım.

Cevap: x=

Ek 4. Önerilen görevler listesinden, sınırlı işlevler yöntemi kullanılarak çözülebilecekleri seçin. 1. x 2 -4 denklemini çözün x=(2-cos
2. x eşitsizliğinin tamsayı çözümlerinin sayısını bulun 2 ctg 2
3. Denklemi çözün
4. Denklem 3'ü çözün-(5. 16'nın 2 ≥0 eşitsizliğinin 3. koşulu sağlayan tamsayı çözümlerinin sayısını bulun. tg 2
6. Denklemi çözün
7. -25x 2 +40x-23=( denklemini çözünçünkü
8. x denkleminin köklerinin çarpımını bulun
9. Denklemi çözün
10. Denklem 3'ü çözünçünkü 2

Kendi kendine test sayfası. Ek 5. 1. Denklemi çözün Çözüm: çünkü o zaman çünkü ve daha sonra
bir denklem sistemi elde ederiz

ilk denklemi çöz, x='i elde et, bu değeri ikinci denklemde yerine koy

2 . Denklemi çözün 3- cos 2 Çözüm: çünkü o zaman çünkü ve daha sonra
bir denklem sistemi elde ederiz

ikinci denklemi çöz, x= elde et, bu değeri birinci denklemde yerine koy

bu, x='in orijinal denklemin bir çözümü olduğu anlamına gelir. Cevap: x=
3. x eşitsizliğinin tamsayı çözümlerinin sayısını bulun 2 +7х-8≤0, koşulu karşılıyor ctg 2 Çözüm: çünkü ve sonra x'in izin verilen herhangi bir değeri için sıfırları bulacağız ikinci dereceden üç terimli Vieta teoremine göre eşitsizliği aralık yöntemini kullanarak çözüyoruz
O. Biz biliyoruz ki
x'in tam sayı değerleri elenen sayılardır Cevap: 8 tam sayı çözümü 4. 16'nın 2 ≥0 eşitsizliğinin 3. koşulu sağlayan tamsayı çözümlerinin sayısını bulun tg 2 Çözüm: çünkü ve sonra x'in izin verilen herhangi bir değeri için, ifadenin sıfırlarını buluruz, x = ve x = Aralık yöntemini kullanarak eşitsizliği çözeriz
O. Biz biliyoruz ki

x'in tam sayı değerleri elenen sayılardır Cevap: 7 tam sayı çözümü
Ek 6.

Fonksiyonların monotonluğunu kullanma yöntemi. Aşağıdaki gibi bir denklemi çözerken f(x)=g(x) bazı durumlarda, y= f(x) ve y= g(x) fonksiyonlarının monotonluğunu kullanan etkili bir yöntem, eğer y= f(x) fonksiyonu sürekliyse ve segmentte artar (azalır) A≤ X ≤ B, ve у= g(x) fonksiyonu süreklidir ve aynı parça üzerinde azalır (artır), bu durumda parça üzerinde f(x)=g(x) denklemi oluşur A≤ X ≤ B Birden fazla kökü olamaz, bu da ya denklemin tek kökünü seçimle bulmaya çalışmak ya da böyle bir kökün olmadığını göstermek gerektiği anlamına gelir. Bu yöntem özellikle f(x) = g(x) denkleminin her iki tarafının ortak çalışma için "uygunsuz" fonksiyonlar olduğu durumda etkilidir. Yorum: Eğer fonksiyon y= f(x) artar ve y= g(x) fonksiyonu azalır A≤ X ≤ B Ve burada F(a)>G(A), o zaman denklemin kökleri arasında A≤ X ≤ B HAYIR.

Örnek: Denklemi çözünÇözüm: Bölge kabul edilebilir değerler denklemler x'tir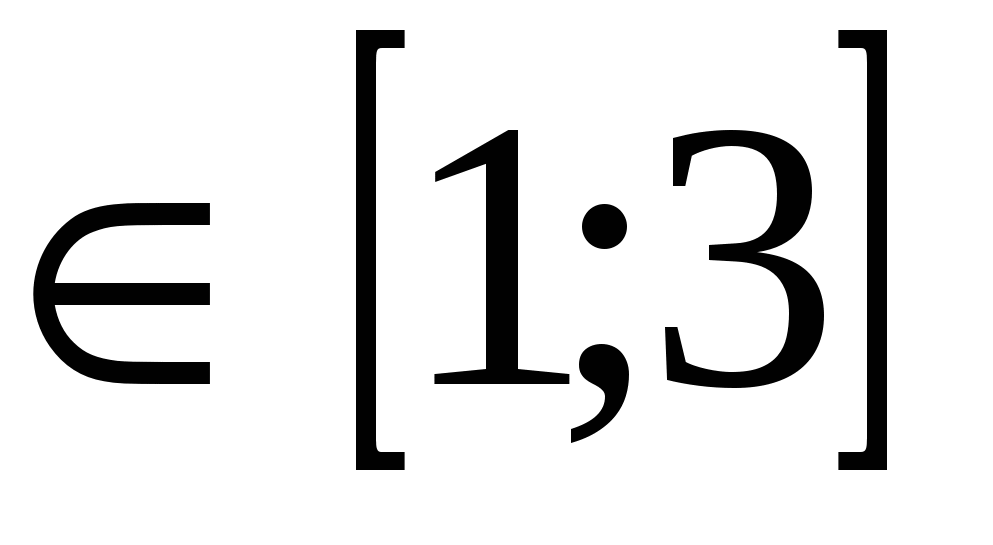
. Bu bölgede denklemin sol tarafının arttığını, sağ tarafının ise azaldığını görmek kolaydır; işlevF(X)=
artıyor ve fonksiyonG(X)=
- azalıyor. Bu bakımdan orijinal denklemin yalnızca bir kökü olabilir (eğer varsa). Seçim yaparak denklemin bu kökünü buluruz x = 2.Cevap: x=2
Fonksiyonel denklemleri çözme yöntemi. En çok karmaşık görevler Birleşik Devlet Sınavı, çözümü formdaki fonksiyonel denklemlerin dikkate alınmasına indirgenen sorunları içerir. f(f(….f(x)…))=x veya f(g(x))=f(h(x))), burada f(x),g(x),h(x) bazı fonksiyonlardır ve n≥ 2
Bu fonksiyonel denklemleri çözme yöntemleri birçok teoremin uygulanmasına dayanmaktadır, bunlardan birini ele alalım.
Teorem 1. Denklemin kökleri F(X)=0 denklemin kökleridir f(f(….f(x)…))=x
Örnek: Denklemi çözün x=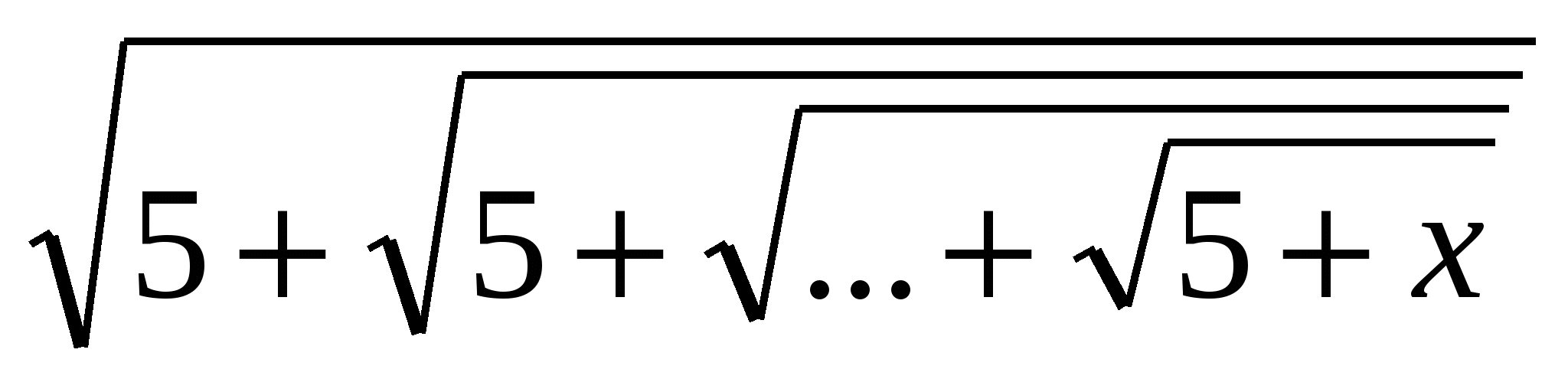
, Nerede Kare kök alınmışNbir kez veN≥ 1 Çözüm: Sorun koşullarından şu sonuç çıkıyor: x> 0. izin verF(X)=
, o zaman denklemimiz fonksiyonel olarak temsil edilebilir F( F(…. F( X)…))= X. x'ten beri> 0 işleviF(X)= artar veF(X) > 0 ise denklem x= denkleme eşdeğerdirF(X)= X, yani =x, pozitif çözümü x=
Cevap: x=

“Bir fonksiyonun tanım alanı” - İkinci dereceden bir fonksiyonun tanım alanı herhangi bir gerçek sayıdır. Bir fonksiyona logaritmik denir, eğer değişken miktar logaritma işaretinin altında duruyor. Logaritmik fonksiyon. Değişkeni üslü olan fonksiyona üstel denir. İkinci dereceden fonksiyon.

"Fonksiyonların genel özellikleri" - Genel Özellikler işlevler. Fonksiyonun tanım tanım kümesini bulun. Hatta işlev. Bu fonksiyonun çift mi yoksa tek mi olduğu. Grafiği kullanarak fonksiyonun değer kümesini belirleyin. Grafiği kullanarak X'in değerlerini belirleyin. Grafiği kullanarak fonksiyondaki azalma aralıklarını belirleyin. f(x) fonksiyonu artıyor. y=f(x) fonksiyonu verilmiştir.

“Artan ve azalan fonksiyon” - Artan ve azalan sinüs fonksiyonu. Başka bir örneğe bakalım. Azalan kosinüs aralıkları segmentlerdir, n bir tamsayıdır. Örneğin f fonksiyonu b>a?0 aralığında çift ve artan olsun. Artan ve azalan fonksiyonlar. Artan ve azalan kosinüs fonksiyonu. Aşağıdaki şekilde [-1;10] ​​aralığında tanımlanan bir fonksiyonun grafiği gösterilmektedir.

"Sürekliliğin Uygulanması" - İfadenin Anlamı. Geometrik anlam türev. Aralık yöntemi. Fonksiyonun grafiğine teğet olan denklemi yazınız. Bir fonksiyonun grafiğine teğet. Grafik teğete yakındır. Formül. Formülü kullanarak hesaplayalım. Belirli bir M noktasında eğriye teğet, NM sekantının sınırlayıcı konumudur. Hiperbol.

“Fonksiyonun ekstremumu” - Gaz basıncının sıcaklığa bağlılığı. Ders konusu: “Artan ve azalan fonksiyonların işaretleri. Ölçek. Devre açıldığında akım gücündeki değişiklik. Bir fonksiyonun ekstremuma kadar incelenmesi". Değiştirmek alternatif akım. Plan: Akımın gerilime bağımlılığı. Gaz basıncının hacme bağımlılığı. Konu: “Artan ve azalan fonksiyonların işaretleri.

“Fonksiyonlar ve özellikleri” - Bağımsız değişkene argüman denir. Artan fonksiyon. Bir fonksiyonun tanımı. Çift ve tek fonksiyonlar. Fonksiyonun monotonluğu. Bağımlı değişkenin değerlerine fonksiyonun değerleri denir. Bağımsız değişkenin tüm değerleri, -D (f) fonksiyonunun tanım alanını oluşturur. 1. Fonksiyon değerleri pozitiftir.

Toplamda 23 sunum var

Fonksiyonların özelliklerinin denklem ve eşitsizliklerin çözümüne uygulanması Çalışma, denklemde yer alan fonksiyonların sınırlılık özelliğine (eşitsizlik) dayanarak denklemleri ve eşitsizlikleri çözmek için standart olmayan yöntemlerden birine ayrılmıştır. Önerdiğim problemler, öğrencileri Birleşik Devlet Sınavına hazırlamak için ayrılan derslerde (üç veya dört ders) değerlendirilebilir veya ders başına bir veya iki problem kullanılabilir ve bu materyal aynı zamanda seçmeli bir derste de kullanılabilir (veya seçmeli ders dersinde).

Bir fonksiyonun değer aralığını bulurken, bir fonksiyonun en büyük ve en küçük değerlerini bulurken sınırlılık özelliğinin uygulanması. 1. Fonksiyonun değer aralığını belirtin: 2. Fonksiyonun değer aralığını belirtin: 3. Fonksiyonun değer aralığını belirtin: 4. Belirleyin en küçük değer fonksiyonlar: y = 5.Fonksiyonun en küçük değerini belirtin: 6.Fonksiyonun değer aralığını belirtin:. 7.Belirtin en yüksek değer işlevler: aralıkta . 8. Fonksiyonun en büyük değerini bulun:

Sınırlı işlev. Fonksiyonun tüm değerleri belirli bir a sayısından az değilse, fonksiyona aşağıda sınırlı denir. f(x)a. Bir fonksiyonun tüm değerleri belirli bir A sayısından büyük değilse, bir fonksiyonun yukarıdan sınırlı olduğu söylenir. f(x)A. Bir fonksiyon hem alttan hem de üstten sınırlı ise buna sınırlı denir. y y y x x xx m M m M

Bir fonksiyonun değer kümesini bulun: Çözüm. Temel kullanımı trigonometrik özdeşlik ve kosinüs formülü çift ​​açı, şunu buluruz: Let t=sinx, -1 Daha sonra çözüm, [-1;1] segmentindeki y= fonksiyonunun değerler kümesini bulmaya gelir. Fonksiyonun grafiği, dalları yukarı doğru yönlendirilmiş bir paraboldür, parabolün tepesi (-1;-1), dolayısıyla [-1;1] segmentinde fonksiyon artar. Dolayısıyla minimum değerini t=-1, y=-1'de, en büyük değerini ise t=1, y=3'te alır. Cevap: E(y)=[-1;3]. =

Fonksiyonun aralıktaki en büyük ve en küçük değerini bulun. Çözüm. Kesrin paydası en küçük değeri aldığında y fonksiyonu en büyük değeri alır. Paydaya bakalım. Fonksiyonlar artıyor, dolayısıyla toplamları artan bir fonksiyondur, yani en küçük değerini parçanın sol ucunda, x = 1'de alır. en küçük değer 5'tir. Dolayısıyla orijinal fonksiyonun en büyük değeri 8'dir. Cevap: 8.

BİR İŞLEVİN EN BÜYÜK DEĞERİNİ BULMAK İÇİN SINIRLI ÖZELLİĞİNİN KULLANILMASI Bu işlev en büyük değeri alır ancak ve ancak üsdeki fonksiyon en büyük değeri alırsa: Fonksiyonun en büyük tamsayı değerini belirtin Haydi dönüştürelim: Fonksiyonun en büyük değeri 4 olduğundan, orijinal fonksiyonun en büyük değeri Cevap: Çözüm.

Fonksiyonların sınırlılık özelliğinin denklem ve eşitsizliklerin çözümüne uygulanması ANA YÖNTEM (TAHMİN YÖNTEMİ) Majör yöntemin ana fikri aşağıdaki gibidir: f(x)=g(x) denklemini ele alalım ve orada f(x) ve g(x) tanımındaki herhangi bir x için f(x) M ve g(x) M'ye sahip olduğumuz bir M sayısıdır. Bu durumda f(x)=g(x) denklemi şu şekildedir: sisteme eşdeğer

Denklemleri çöz

Denklemi çözün Çözüm: Çözüm: Denklemin her iki tarafını da değerlendirelim. X'in tüm değerleri için aşağıdaki eşitsizlikler doğrudur. Dolayısıyla bu denklem sisteme eşdeğerdir: x = 0 olduğunda ikinci denklem gerçek bir eşitliğe dönüşür, yani denklemin kökü x = 0'dır. Cevap: x = 0.

Denklemi çözün. Çözüm. Fonksiyonu ele alalım. Parabolün tepe noktasının koordinatlarını bulalım. x 0 = 7, y 0 = 25. Dallar yukarıya doğru yönlendirildiğinden fonksiyonun en küçük değeri 25'tir. O halde f(x) 25 olduğundan. Açıkçası, 1. Bu, ikinci terimin 1'e ve birincisinin 0'a eşit olması koşuluyla orijinal denklemin kökleri olduğu anlamına gelir. x-7=0, x=7 X=7 olduğunda ikinci terim eşittir 1'e kadar. Dolayısıyla x=7 denklemin köküdür.

Denklemin çözümünü çözün. Denklemin kökünü tahmin etmek kolaydır - x = 1'dir. Ancak monotonluk değerlendirmelerinden bunun benzersizliğini kanıtlamak mümkün değildir çünkü denklemin ne sol ne de sağ tarafı monoton fonksiyonlar değildir. Burada farklı bir fikir kullanılmış. Denklemi dönüştürelim: Ortaya çıkan denklemin sağ tarafındaki en büyük değer 1'e eşit olup x = 1 noktasında alınmaktadır. Logaritma altındaki ifade x > 0 için eşittir. Dolayısıyla sol- el tarafı minimum değerine x = 1'de ulaşır, bu da 1'e eşittir. Sonuç: eşitlik ancak ve ancak her iki parça aynı anda 1'e eşit olduğunda, yani x = 1 olduğunda sağlanır. 0. Dolayısıyla sol taraf minimum değerine x = 1'de ulaşır, bu da 1'e eşittir. Sonuç: Eşitlik ancak ve ancak her iki tarafın da aynı anda 1'e eşit olması durumunda sağlanır, yani x = 1.">

Bu kökleri yerine koyarak ilk eşitliğin geçerliliğini kontrol edelim. Denklemi Çözerken Çözüm. Denklemi çözmek için parçalarını değerlendirelim: Bu nedenle eşitlik ancak şu şartla mümkündür: İlk önce ikinci denklemi çözeriz: Bu denklemin kökleri ve şunu elde ederiz: (gerçek eşitlik). Yani bu denklemin tek kökü x = 0'dır. Cevap: 0. x = -1 için elimizde: (gerçek bir eşitlik değil) bulunur. cos() [-1;1] cos 2 () . bir ve negatif olmayan bir sayının toplamı.

Denklemi çözün. Çözüm. (ikisinin toplamı karşılıklı sayılar). Sonuç olarak, fonksiyon süreklilik nedeniyle aralıktaki tüm değerleri alır. Fonksiyonu değerlendirelim. Grafik bir paraboldür, yukarıya doğru dallanır, en küçük değer 3'tür. Bu, h(y)'nin en büyüğünü aldığı ve 3'e eşit olduğu anlamına gelir. Dolayısıyla orijinal denklem sisteme eşdeğerdir.

(Çünkü:). Denklemi çözün Denklemin sol tarafı sağ taraf için (karşılıklı olarak ters iki sayının toplamının eşitsizliğinden dolayı) sağlandığı için Denklemin çözümleri ancak ve ancak iki koşulun aynı anda sağlanması durumunda olur Çözme son sistem 0,5'ten 2'ye kadar bir değer alırız. Cevap: Çözüm. Denklemin her iki tarafını da değerlendirelim.

Her biri için eşitsizliğin bir çözümü olan a parametresinin tüm değerlerini bulun. Eşitsizliğin her iki tarafını da tahmin edelim. Bunu yapmak için, tam kareyi vurgulayarak eşitsizliğin sağ tarafını dönüştürürüz. İkinci dereceden fonksiyon tepe noktasında en küçük değeri alır, 4'e eşittir ve a = -6/7'de elde edilir. Eşitsizliğin sol tarafındaki değerler kümesi bir aralık oluşturur, dolayısıyla en büyük değer 4'tür. Bu, eşitsizliğin her iki tarafın eşit olması durumunda ve yalnızca a = -6/7 olması durumunda karşılandığı anlamına gelir. Cevap: a=-6/7..

Her biri için denklemin çözümleri olan a parametresinin tüm değerlerini bulun. Bu çözümleri bulun. Çözüm. Denklemi şu şekilde yeniden yazalım: X'in tüm değerleri için ifade bu nedenledir. X'in tüm değerleri için ifade ve'dir. Bu yüzden. Dolayısıyla denklemin sol tarafı 4'ten az, sağ tarafı ise 4'ten fazla değildir. Cevap: x = 5/7 ve a = -4/9 sistemini elde ederiz.

Denklemin kökleri olmayan P parametresinin tüm değerlerini bulun. Çift açılı kosinüs formülünü kullanarak ifadeyi dönüştürüyoruz. P, denklemin sol tarafındaki değer aralığına ait değilse denklemin kökleri olmayacaktır. f(x)= fonksiyonunu ele alalım ve değerlendirelim. Bu nedenle, f(x) Fonksiyonu süreklidir ve tüm değerlerini alır: sinx=0, f(x)=-9 ve eğer sinx=1 ise f(x)=17, yani. E(f)=[-9;17] Bu parçayı sayı doğrusundan çıkarıyoruz ve cevabı alıyoruz. Cevap:

İşlev monotonluğunu kullanma Denklemleri ve eşitsizlikleri çözerken aşağıdaki teorik gerçeklere dayanır:

1. Kesinlikle monoton fonksiyon her değeri tam olarak bir kez alır.
2. Eğer aynı aralıkta bir fonksiyon artarken diğeri azalıyorsa, grafikleri ya yalnızca bir kez kesişecek ya da hiç kesişmeyecektir; bu, F(x)=G(x) denkleminin en fazla bir çözümü olduğu anlamına gelir.
3. Belirli bir aralıkta işlevlerden biri azalırsa (artırılırsa), diğeri ise sabit değerler ise F(x)=G(x) denkleminin ya tek kökü vardır ya da kökü yoktur.

Örnek

Denklemi çözün:\((x^3) = 2 - x\)

\(f(x) = (x^3)\) ve \(g(x) = 2 - x.\) fonksiyonlarını düşünün

f(x) fonksiyonu tüm tanım bölgesi boyunca artar ve g(x) fonksiyonu tanım bölgesi boyunca azalır. Bu nedenle bu denklemin hiçbir değeri yoktur.

birden fazla kök.

Seçim yaparak x=1 olduğunu buluruz. Kontrol ederek x=1'in gerçekten de denklemin kökü olduğuna ikna olduk.

Kontrol edin: 13=2-1; 1=1.

Eşlik işlevini kullanma

Herhangi bir \(x \in D\) için bile f(x) fonksiyonu çağrılır

eşitlik geçerlidir: \(f(- x) = f(x).\)

Parite fonksiyonlarının incelenmesi aşağıdaki ifadelerle kolaylaştırılmıştır:

Çift (tek) fonksiyonların toplamı

Xia çift (tek) işlevi.

·İki çift veya iki tek fonksiyonun çarpımı bir çift fonksiyondur.

Çift ve çarpımı Tek işlev garip bir fonksiyondur.

·Eğer f fonksiyonu çift (tek) ise, o zaman \(\frac(1)(f)\) fonksiyonu

tek çift).

Örnek

a'nın bir değeri için denklem şu şekilde olabilir: \(2(x^8) - 3a(x^6) + 4(x^4) - a(x^2) = 5\) 5 kökü var mı?

Haydi belirtelim \(f(x) = 2(x^8) - 3a(x^6) + 4(x^4) - a(x^2) = 5,\) burada f(x) - eşit işlev. Bu denklemin kökü x0 ise (-x0) da bir köktür. X=0 değeri denklemin kökü değildir. Bu nedenle herhangi bir denklem için bu denklemin kök sayısı

gerçek ve çift olduğundan 5 kökü yoktur

İşlev Kapsamını Kullanma

Bir fonksiyonun etki alanı tüm geçerli olanların kümesidir. gerçek değerler fonksiyonun tanımlandığı argüman x (değişken x). Tanım alanı bazen izin verilen alan olarak da adlandırılır.

fonksiyon değerleri. Bir işlevi bulmak için bu yazışmayı analiz etmeniz ve karşılaşılan yasaklanmış işlemleri (bölme) belirlemeniz gerekir.

sıfır, rasyonel bir kuvvete yükseltiliyor

Negatif sayı, logaritmik işlemler negatif sayılar ve benzeri.). Bazen bilgi bir denklemin (veya eşitsizliğin) eşit olmadığını kanıtlamanıza olanak tanır.

çözümler ve bazen sayıları doğrudan değiştirerek bir denklemin (veya eşitsizliğin) çözümlerini bulmanızı sağlar.

Eşitsizliği çöz \(\sqrt (x + 3) + \sqrt((9 - x))< \sqrt 3 \)

Eşitsizliğin ODZ'si aralıktaki tüm x'tir \(- 3 \leqslant x \leqslant 9.\)

Bu kümeyi iki aralığa bölelim ve \(0 \leqslant x \leqslant 9.\)

Aralıktan x için \(- 3 \leqslant x \leqslant 0\) sahibiz:

\(\begin(toplanmış) \sqrt (x + 3) \geqslant 0; \\ \sqrt((9 - x)) \geqslant \sqrt(9); \\ \sqrt(9) = \sqrt 3 . \ \\son(toplandı)\)

Dolayısıyla bu aralıkta, dolayısıyla eşitsizliğin bu aralıkta çözümü yoktur.

X'in \(0 \leqslant x \leqslant 9\)'a ait olduğunu varsayalım, o zaman:

\(\begin(toplandı) \sqrt (x + 3) \geqslant \sqrt 3 ; \\ \sqrt((9 - x)) \geqslant 0. \\ \end(toplandı) \)

Buradan, \(\sqrt (x + 3) + \sqrt((9 - x)) \geqslant \sqrt 3 \) böyle bir x için ve dolayısıyla bu aralıkta eşitsizliğin de çözümü yoktur.

Yani eşitsizliğin çözümü yoktur.

Özellik kısıtlamasını kullanma. Denklemleri ve eşitsizlikleri çözerken, bir fonksiyonun belirli bir kümenin altından veya üstünden sınırlı olması özelliği çoğu zaman belirleyici bir rol oynar.

Herhangi bir \(x \in D\) için f(x)\(\leqslant \) C eşitsizliğini sağlayacak bir C sayısı varsa, o zaman f fonksiyonunun D kümesinde yukarıdan sınırlandığı söylenir.

Herhangi bir sayı için f(x) ≥с eşitsizliğinin sağlandığı bir c sayısı varsa, f fonksiyonunun D kümesinde alttan sınırlı olduğu söylenir.

Hem yukarıdan hem de aşağıdan sınırlı olan bir fonksiyona D kümesinde sınırlı denir. Geometrik olarak, bir f fonksiyonunun D kümesindeki sınırlılığı, y=f(x) fonksiyonunun grafiğinin c\(\leqslant \ şeridinde yer aldığı anlamına gelir. ) f(x)\( \leqslant\) C.

Denklemi çözün \(\sin ((x^3) + 2(x^2) + 1) = (x^2) + 2x + 2\)

Herkes için gerçek Numara x elimizde \(\sin ((x^3) + 2(x^2) + 1) \leqslant 1,\)\((x^2) + 2x + 2 = ((x + 1)^2) + 1 \geqslant 1.\)

Herhangi bir x değeri için denklemin sol tarafı bir'i aşmadığından ve sağ tarafı da her zaman birden küçük olmadığından, bu denklemin yalnızca x = -1 için bir çözümü olabilir.

x=-1 için elimizde:

\(\begin(toplandı) (x^2) + 2x + 2 = 1; \\ \sin (- 1 + 2 + 1) = \sin 2 \ne 1; \\ \end(toplandı) \)

onlar. Denklemin kökleri yoktur.