Bu çevrimiçi matematik hesaplayıcısı size yardımcı olacaktır Bir denklemi veya eşitsizliği modüllerle çözme. Programı Denklemleri ve eşitsizlikleri modüllerle çözme yalnızca sorunun cevabını vermekle kalmaz, aynı zamanda açıklamalarla ayrıntılı çözüm, yani Sonucun elde edilme sürecini görüntüler.

Bu program ortaöğretim kurumlarındaki lise öğrencileri için hazırlık aşamasında faydalı olabilir. testler ve sınavlar, Birleşik Devlet Sınavından önce bilgiyi test ederken, ebeveynlerin matematik ve cebirdeki birçok problemin çözümünü kontrol etmeleri için. Ya da belki bir öğretmen tutmak ya da yeni ders kitapları satın almak sizin için çok mu pahalı? Yoksa mümkün olduğu kadar çabuk halletmek mi istiyorsunuz? Ev ödevi matematikte mi yoksa cebirde mi? Bu durumda detaylı çözümlere sahip programlarımızı da kullanabilirsiniz.

Bu şekilde kendi eğitiminizi ve/veya eğitiminizi yürütebilirsiniz. küçük kardeşler veya kız kardeşler, sorunların çözüldüğü alandaki eğitim düzeyi arttıkça artar.

|x| veya abs(x) - modül x

Modüllerle bir denklem veya eşitsizlik girin

Bir denklemi veya eşitsizliği çözme

Bu sorunu çözmek için gerekli olan bazı scriptlerin yüklenmediği ve programın çalışmayabileceği tespit edildi.
AdBlock'u etkinleştirmiş olabilirsiniz.
Bu durumda devre dışı bırakın ve sayfayı yenileyin.

Tarayıcınızda JavaScript devre dışı bırakıldı.
Çözümün görünmesi için JavaScript'i etkinleştirmeniz gerekir.
Tarayıcınızda JavaScript'i nasıl etkinleştireceğinize ilişkin talimatları burada bulabilirsiniz.

Çünkü Sorunu çözmek isteyen çok kişi var, talebiniz sıraya alındı.
Birkaç saniye içinde çözüm aşağıda görünecektir.
Lütfen bekleyin saniye...

Eğer sen çözümde bir hata fark ettim, ardından Geri Bildirim Formu'na bu konuda yazabilirsiniz.
Unutma hangi görevi belirtin ne olduğuna sen karar ver alanlara girin.

Oyunlarımız, bulmacalarımız, emülatörlerimiz:

Küçük bir teori.

Modüllü denklemler ve eşitsizlikler

Temel bir okul cebir dersinde modüllü en basit denklemler ve eşitsizliklerle karşılaşabilirsiniz. Bunları çözmek için kullanabilirsiniz geometrik yöntem\(|x-a| \)'nin sayı doğrusunda x ve a noktaları arasındaki mesafe olduğu gerçeğine dayanarak: \(|x-a| = \rho (x;\; a)\). Örneğin, \(|x-3|=2\) denklemini çözmek için sayı doğrusu üzerinde 3. noktadan 2 uzaklıkta olan noktaları bulmanız gerekir. Böyle iki nokta vardır: \(x_1=1 \) ve \(x_2=5\) .

Eşitsizliği çözme \(|2x+7|

Ancak denklemleri ve eşitsizlikleri modüllerle çözmenin ana yolu, "modülün tanımı gereği ortaya çıkarılması" ile ilişkilidir:
if \(a \geq 0 \), ardından \(|a|=a \);
if \(a Kural olarak, modüllü bir denklem (eşitsizlik), modül işaretini içermeyen bir dizi denkleme (eşitsizlikler) indirgenir.

Yukarıdaki tanıma ek olarak aşağıdaki ifadeler kullanılmıştır:
1) Eğer \(c > 0\), o zaman \(|f(x)|=c \) denklemi şu denklem grubuna eşdeğerdir: \(\left[\begin(array)(l) f(x) )=c \\ f(x)=-c \end(dizi)\sağ.
2) Eğer \(c > 0 \), o zaman eşitsizlik \(|f(x)| 3) Eğer \(c \geq 0 \), o zaman \(|f(x)| > c \) eşitsizliği şöyledir: bir eşitsizlikler kümesine eşdeğerdir: \(\left[\begin(array)(l) f(x) c \end(array)\right. \)
4) Eşitsizliğin her iki tarafı \(f(x) ise ÖRNEK 1. \(x^2 +2|x-1| -6 = 0\) denklemini çözün.

Eğer \(x-1 \geq 0\), o zaman \(|x-1| = x-1\) ve verilen denklem formu alır
\(x^2 +2(x-1) -6 = 0 \Rightarrow x^2 +2x -8 = 0 \).
Eğer \(x-1 \(x^2 -2(x-1) -6 = 0 \Rightarrow x^2 -2x -4 = 0 \).
Bu nedenle, verilen denklem belirtilen iki durumun her birinde ayrı ayrı ele alınmalıdır.
1) \(x-1 \geq 0 \) olsun, yani. \(x\geq 1\). \(x^2 +2x -8 = 0\) denkleminden \(x_1=2, \; x_2=-4\) bulunur. \(x \geq 1 \) koşulu yalnızca \(x_1=2\) değeri tarafından karşılanır.
2) \(x-1 Cevap: \(2; \;\; 1-\sqrt(5) \) olsun

ÖRNEK 2. \(|x^2-6x+7| = \frac(5x-9)(3)\) denklemini çözün.

İlk yol(tanım gereği modül genişletme).
Örnek 1'deki gibi akıl yürüterek, verilen denklemin iki koşulun karşılanması durumunda ayrı ayrı dikkate alınması gerektiği sonucuna varıyoruz: \(x^2-6x+7 \geq 0 \) veya \(x^2-6x+7)

1) Eğer \(x^2-6x+7 \geq 0 \), o zaman \(|x^2-6x+7| = x^2-6x+7 \) ve verilen denklem \(x) formunu alır ^2 -6x+7 = \frac(5x-9)(3) \Rightarrow 3x^2-23x+30=0 \). Buna karar verdikten sonra ikinci dereceden denklemşunu elde ederiz: \(x_1=6, \; x_2=\frac(5)(3) \).
\(x_1=6\) değerinin \(x^2-6x+7 \geq 0\) koşulunu karşılayıp karşılamadığını bulalım. Bunu yapmak için yerine koyalım belirlenmiş değer V ikinci dereceden eşitsizlik. Şunu elde ederiz: \(6^2-6 \cdot 6+7 \geq 0 \), yani. \(7 \geq 0 \) gerçek bir eşitsizliktir. Bu, \(x_1=6\)'nın verilen denklemin kökü olduğu anlamına gelir.
\(x_2=\frac(5)(3)\) değerinin \(x^2-6x+7 \geq 0\) koşulunu karşılayıp karşılamadığını bulalım. Bunu yapmak için belirtilen değeri ikinci dereceden eşitsizliğin yerine koyun. Şunu elde ederiz: \(\left(\frac(5)(3) \right)^2 -\frac(5)(3) \cdot 6 + 7 \geq 0 \), yani. \(\frac(25)(9) -3 \geq 0 \) yanlış bir eşitsizliktir. Bu, \(x_2=\frac(5)(3)\) öğesinin verilen denklemin kökü olmadığı anlamına gelir.

2) Eğer \(x^2-6x+7 Değeri \(x_3=3\) koşulu karşılıyorsa \(x^2-6x+7 Değeri \(x_4=\frac(4)(3) \) karşılamıyor \ (x^2-6x+7 koşulu) Yani verilen denklemin iki kökü vardır: \(x=6, \; x=3 \).

İkinci yol.\(|f(x)| = h(x) \) denklemi verilirse, \(h(x) \(\left[\begin(array)(l) x^2-6x+7 = ile \frac (5x-9)(3) \\ x^2-6x+7 = -\frac(5x-9)(3) \end(array)\right \)
Bu denklemlerin her ikisi de yukarıda çözüldü (verilen denklemin ilk çözümü kullanılarak), kökleri şu şekildedir: \(6,\; \frac(5)(3),\; 3,\; \frac(4) )(3)\). Bu dört değerin \(\frac(5x-9)(3) \geq 0 \) koşulu yalnızca iki tanesi tarafından karşılanır: 6 ve 3. Bu, verilen denklemin iki kökü olduğu anlamına gelir: \(x=6 , \; x=3 \ ).

Üçüncü yol(grafik).
1) \(y = |x^2-6x+7| \) fonksiyonunun grafiğini oluşturalım. İlk önce bir \(y = x^2-6x+7\) parabolünü oluşturalım. \(x^2-6x+7 = (x-3)^2-2 \) elimizde. \(y = (x-3)^2-2\) fonksiyonunun grafiği, \(y = x^2\) fonksiyonunun grafiğinden 3 ölçek birim sağa kaydırılarak (yön boyunca) elde edilebilir. x ekseni) ve 2 ölçek birimi aşağı (y ekseni boyunca). Düz çizgi x=3 ilgilendiğimiz parabolün eksenidir. Daha doğru çizim için kontrol noktaları olarak, parabolün tepe noktası olan (3; -2) noktasını, parabolün eksenine göre ona simetrik olan (0; 7) noktasını ve (6; 7) noktasını almak uygundur. .
Şimdi \(y = |x^2-6x+7| \) fonksiyonunun bir grafiğini oluşturmak için, oluşturulan parabolün x ekseninin altında olmayan kısımlarını değiştirmeden bırakmanız ve bu kısmı aynalamanız gerekir. x eksenine göre x ekseninin altında yer alan parabol.
2) Bir grafik oluşturalım doğrusal fonksiyon\(y = \frac(5x-9)(3)\). (0; –3) ve (3; 2) noktalarını kontrol noktası olarak almak uygundur.

Düz çizginin apsis ekseni ile kesiştiği noktanın x = 1.8 noktasının, parabolün apsis ekseni ile kesiştiği sol noktanın sağında yer alması önemlidir - bu nokta \(x=3-\ sqrt(2) \) (çünkü \(3-\sqrt(2 ) 3) Çizime bakılırsa, grafikler iki noktada kesişiyor - A(3; 2) ve B(6; 7). Verilen denklemde x = 3 ve x = 6 noktalarında, her iki durumda da doğru sayısal eşitliğin elde edildiğine inanıyoruz; bu, hipotezimizin doğrulandığı anlamına gelir - denklemin iki kökü vardır: x = 3 ve. x = 6. Cevap: 3;

Yorum. Grafik yöntemi tüm zarafetine rağmen pek güvenilir değil. Ele alınan örnekte, denklemin kökleri tamsayı olduğu için işe yaradı.

ÖRNEK 3. \(|2x-4|+|x+3| = 8\) denklemini çözün

İlk yol
2x–4 ifadesi x = 2 noktasında 0 olur, x + 3 ifadesi de x = –3 noktasında 0 olur. Bu iki nokta sayı doğrusunu üç aralığa böler: \(x

İlk aralığı düşünün: \((-\infty; \; -3) \).
Eğer x İkinci aralığı düşünün: \([-3; \; 2) \).
If \(-3 \leq x Üçüncü aralığı düşünün: \( [ 3/2 ; ∞ )

Yöntem eşdeğer dönüşümler denklem çözerken de kullandık | f(x)| = | g(x)|.

KARMAŞIK MODÜLLÜ DENKLEMLER

Diğer bir denklem türü ise “karmaşık” modülü olan denklemlerdir. Bu tür denklemler, "bir modül içinde modüller" içeren denklemleri içerir. Bu tür denklemler kullanılarak çözülebilir çeşitli metodlar.

Örnek 1.

Denklemi çözün ||||x| – |–2| –1| –2| = 2.

Çözüm.

Bir modülün tanımı gereği elimizde:

İlk denklemi çözelim.

||| x |–2| –1| = 4

| x | – 2 = 5;

| x | = 7;

x = 7.

İkinci denklemi çözelim.

||| x | –2| –1| = 0,

|| x | –2| = 1,

| x | –2 = 1,

| x | = 3 ve | x | = 1,

x = 3; x = 1.

Cevap 1; 3; 7.

Örnek 2.

|2 – |x + 1|| denklemini çözün = 3.

Çözüm.

Denklemi yeni bir değişken ekleyerek çözelim.

Let | x + 1| = y, sonra |2 – y | = 3, dolayısıyla

Ters değiştirme işlemini yapalım:

(1) | X + 1| = –1 – çözüm yok.

(2) | x + 1| = 5

CEVAP: –6; 4.

Örnek3.

Denklemin kaç kökü var | 2 | x | -6 | = 5 - x?

Çözüm. Denklem şemalarını kullanarak denklemi çözelim.

Denklem | 2 | x | -6 | = 5 sisteme eşdeğerdir:

MBOU Ortaokulu No. 17, İvanovo

« Modüllü denklemler"
Metodolojik gelişim

Derlenmiş

Matematik öğretmeni

Lebedeva N.V.

20010

Açıklayıcı not

Bölüm 1. Giriş

Bölüm 2. Temel özellikler Bölüm 3. Bir sayının modülü kavramının geometrik yorumu Bölüm 4. y = |x| fonksiyonunun grafiği Bölüm 5. Sözleşmeler

Bölüm 2. Modül içeren denklemlerin çözülmesi

Bölüm 1. |F(x)| formundaki denklemler = m (en basit) Bölüm 2. F(|x|) = m formundaki denklemler Bölüm 3. |F(x)| formundaki denklemler = G(x) Bölüm 4. |F(x)| formundaki denklemler = ± F(x) (en güzel) Bölüm 5. |F(x)| formundaki denklemler = |G(x)| Bölüm 6. Çözüm örnekleri standart olmayan denklemler Bölüm 7. |F(x)| formundaki denklemler + |G(x)| = 0 Bölüm 8. |a 1 x ± b 1 | formundaki denklemler ± |a 2 x ± inç 2 | ± …|a n x ± inç n | = m Bölüm 9. Birkaç modül içeren denklemler

Bölüm 3. Modüllü çeşitli denklemlerin çözümüne örnekler.

Bölüm 1. Trigonometrik denklemler Bölüm 2. Üstel denklemler Bölüm 3. Logaritmik denklemler Bölüm 4. İrrasyonel denklemler Bölüm 5. Ödevler artan karmaşıklık Alıştırmaların cevapları Kaynakça

Açıklayıcı not.

Gerçel sayının mutlak değeri (modülü) kavramı onun temel özelliklerinden biridir. Bu kavram fiziksel, matematiksel ve teknik bilimlerin çeşitli bölümlerinde yaygındır. Matematik derslerinin öğretimi uygulamasında lise Rusya Federasyonu Savunma Bakanlığı Programı uyarınca “sayıların mutlak değeri” kavramıyla defalarca karşılaşılmaktadır: 6. sınıfta modülün tanımı ve geometrik anlamı tanıtılmaktadır; 8. sınıfta kavram oluşturulur mutlak hata, modül içeren en basit denklemlerin ve eşitsizliklerin çözümü dikkate alınır, aritmetiğin özellikleri incelenir kare kök; 11. sınıfta kavram “Kök” bölümünde yer almaktadır. N-inci derece."Öğretim deneyimi, öğrencilerin bu materyal hakkında bilgi gerektiren görevleri çözmede sıklıkla zorluklarla karşılaştıklarını ve çoğu zaman bunları tamamlamaya başlamadan atladıklarını göstermektedir. Metinlerde sınav görevleri Benzer görevler 9. ve 11. sınıf dersleri için de yer almaktadır. Ayrıca üniversitelerin okul mezunlarına yüklediği gereksinimler de farklılık göstermektedir. yüksek seviye okul müfredatının gereklerinden daha fazlası. Yaşam için modern toplum Belirli zihinsel becerilerde kendini gösteren matematiksel düşünme stilinin geliştirilmesi oldukça önemlidir. Modüllerle problem çözme sürecinde genelleme ve belirleme, analiz, sınıflandırma ve sistemleştirme, analoji gibi teknikleri kullanma becerisi gereklidir. Bu tür görevleri çözmek, ana bölümler hakkındaki bilginizi test etmenize olanak tanır okul kursu, seviye mantıksal düşünme, ilk araştırma becerileri. bu iş Bir modül içeren denklemlerin çözülmesi bölümlerinden birine ayrılmıştır. Bu oluşmaktadır üç bölüm. Birinci bölümde temel kavramlar ve en önemli teorik hususlar tanıtılmaktadır. İkinci bölümde bir modül içeren dokuz ana denklem türü öneriliyor, bunları çözme yöntemleri tartışılıyor ve örnekler inceleniyor farklı seviyeler zorluklar. Üçüncü bölümde daha karmaşık ve standart dışı denklemler (trigonometrik, üstel, logaritmik ve irrasyonel) sunulmaktadır. Her denklem türü için alıştırmalar vardır. bağımsız karar(cevaplar ve talimatlar ektedir). Bu çalışmanın temel amacı sağlamaktır. metodolojik yardımÖğretmenlerin derslere hazırlanmalarında ve seçmeli derslerin düzenlenmesinde. Malzeme aynı zamanda şu şekilde de kullanılabilir: öğretim yardımı lise öğrencileri için. Çalışmada önerilen görevler ilginçtir ve çözülmesi her zaman kolay değildir; öğrenme motivasyonuÖğrencilerin daha bilinçli olmalarını, yeteneklerini test etmelerini ve okul mezunlarının üniversitelere girişe hazırlık seviyelerini geliştirmelerini sağlamak. Önerilen alıştırmaların farklı bir seçimi, materyale hakim olmanın üreme düzeyinden yaratıcı olana geçişi ve standart dışı problemleri çözerken bilginizi nasıl uygulayacağınızı öğretme fırsatını içerir.

Bölüm 1. Giriş.

Bölüm 1. Mutlak değerin belirlenmesi .

Tanım : Gerçek bir sayının mutlak değeri (modülü) A isminde negatif olmayan sayı: A veya -A. Tanım: │ A │ Giriş şu şekildedir: "a sayısının modülü" veya "a sayısının mutlak değeri"

│ a, eğer a > 0 ise

│a│ = │ 0, eğer a = 0 (1)

│ - ve eğer
Örnekler: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1
İfade modülünü genişletin:
a) │x - 8│, eğer x > 12 ise b) │2x + 3│, eğer x ≤ -2 │x – 8│= x – 8 │ 2x + 3│= - 2x – 3
Bölüm 2. Temel özellikler.
Mutlak değerin temel özelliklerini ele alalım. Mülk #1: Zıt sayılar var eşit modüller, yani │а│=│- а│ Eşitliğin doğru olduğunu gösterelim. Sayının tanımını yazalım - A : │- bir│= (2) (1) ve (2) numaralı kümeleri karşılaştıralım. Açıkçası, sayıların mutlak değerlerinin tanımları A Ve - A eşleştir. Buradan, │а│=│- а│
Revize ederek aşağıdaki özellikler Kanıtları aşağıda verildiği için kendimizi onların formülasyonuyla sınırlayacağız. Özellik #2: Tutarın mutlak değeri sonlu sayı gerçek sayılar terimlerin mutlak değerlerinin toplamını aşmaz: │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │+ … + │а n │ Özellik #3: İki reel sayı arasındaki farkın mutlak değeri, mutlak değerlerinin toplamını aşmaz: │а - в│ ≤│а│+│в│ Mülk #4: Sonlu sayıda gerçek sayıların çarpımının mutlak değeri, faktörlerin mutlak değerlerinin çarpımına eşittir: │а·в│=│а│·│в│ Mülk #5: Reel sayıların bölümünün mutlak değeri, mutlak değerlerinin bölümüne eşittir:

Bölüm 3. Bir sayının modülü kavramının geometrik yorumu.

Her reel sayı, sayı doğrusu üzerinde bir noktaya ilişkilendirilebilir. geometrik görüntü gerçek sayı verilmiştir. Sayı doğrusu üzerindeki her nokta orijine olan uzaklığına karşılık gelir, yani. segmentin başlangıç noktasından belirli bir noktaya kadar olan uzunluğu. Bu mesafe her zaman negatif olmayan bir değer olarak kabul edilir. Bu nedenle, karşılık gelen segmentin uzunluğu geometrik yorumlama Belirli bir gerçek sayının mutlak değeri

Sunulan geometrik çizim, 1 numaralı özelliği açıkça doğrulamaktadır; modüller zıt sayılar eşittir. Buradan eşitliğin geçerliliği kolaylıkla anlaşılmaktadır: │х – а│= │а – x│. m ≥ 0, yani x 1,2 = ± m olan │х│= m denkleminin çözümü de daha açık hale gelir. Örnekler: 1) │х│= 4 x 1,2 = ± 4 2) │х - 3│= 1

x 1,2 = 2; 4

Bölüm 4. y = │х│ fonksiyonunun grafiği

Bu fonksiyonun tanım kümesi tamamen gerçek sayılardır.

Bölüm 5. Sözleşmeler.

Gelecekte denklem çözme örnekleri dikkate alınırken aşağıdakiler kullanılacaktır: semboller: ( - sistemin işareti [ - bütünlüğün işareti Bir denklem sistemini (eşitsizlikleri) çözerken, sistemde yer alan denklemlerin (eşitsizliklerin) çözümlerinin kesişimi bulunur. Bir denklem kümesini (eşitsizlikler) çözerken, denklem kümesinde (eşitsizlikler) bulunan çözümlerin birliği bulunur.

Bölüm 2. Modül içeren denklemlerin çözümü.

Bu bölümde şunlara bakacağız: cebirsel yöntemler Bir veya daha fazla modül içeren denklemleri çözme.

Bölüm 1. │F(x)│= m formundaki denklemler

Bu tür bir denkleme en basit denir. Yalnızca m ≥ 0 olması durumunda bir çözümü vardır. Modül tanımı gereği, orijinal denklem iki denklemden oluşan bir diziye eşdeğerdir: │ F(x)│=M

Örnekler:
№1. Denklemi çözün: │7х - 2│= 9

Cevap: x 1 = - 1; X 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

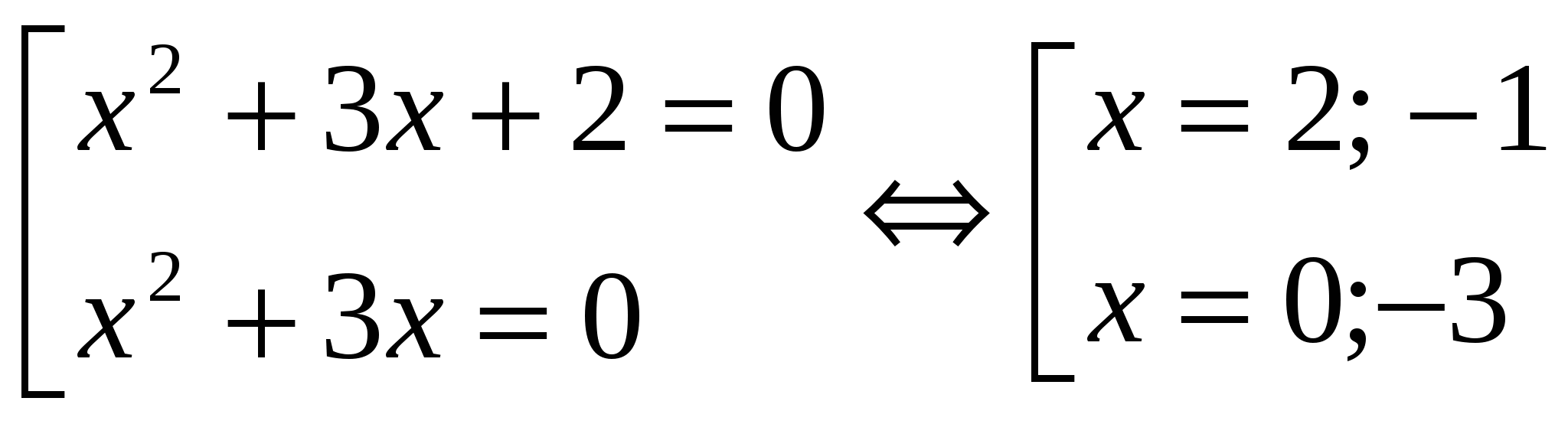x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x2 = -3 Cevap: Köklerin toplamı -2.№3
│x 4 -5x 2 + 2│= 2 x 4 – 5x 2 = 0 x 4 – 5x 2 + 4 = 0 x 2 (x 2 – 5) = 0 x 2 = m, m ≥ 0 x = 0 olsun ; ±√5 m 2 – 5 m + 4 = 0 m = 1; 4 – her iki değer de m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 koşulunu karşılamaktadır Cevap: Denklemin kök sayısı 7. Egzersizler:
№1. Denklemi çözün ve köklerin toplamını belirtin: │х - 5│= 3 №2 . Denklemi çözün ve daha küçük olan kökü belirtin: │x 2 + x│= 0 №3 . Denklemi çözün ve büyük kökü belirtin: │x 2 – 5x + 4│= 4 №4 .Denklemleri çözün ve belirtin bütün kök: │2x 2 – 7x + 6│= 1 №5 .Denklemi çözün ve kök sayısını belirtin: │x 4 – 13x 2 + 50│= 14

Bölüm 2. F(│х│) = m formundaki denklemler

Sol taraftaki fonksiyon argümanı modül işaretinin altındadır ve sağ taraf değişkenden bağımsızdır. Bu tür denklemleri çözmenin iki yolunu ele alalım. 1 yol: Mutlak değerin tanımı gereği, orijinal denklem iki sistemin birleşimine eşdeğerdir. Her birinde bir alt modüler ifadeye bir koşul uygulanır. F(│х│) =M

F(│x│) fonksiyonu tüm tanım kümesi boyunca çift olduğundan, F(x) = m ve F(- x) = m denklemlerinin kökleri zıt sayı çiftleridir. Bu nedenle sistemlerden birini çözmek yeterlidir (örnekler bu şekilde ele alındığında tek sistemin çözümü verilecektir). Yöntem 2: Yeni bir değişken ekleme yönteminin uygulanması. Bu durumda, a ≥ 0 olmak üzere │x│= a gösterimi kullanılır. Bu method tasarım açısından daha az hacimli.
Örnekler: №1 . Denklemi çözün: 3x 2 – 4│x│= - 1 Yeni bir değişkenin tanıtımını kullanalım. a ≥ 0 olmak üzere │x│= a'yı gösterelim. 3a 2 - 4a + 1 = 0 denklemini elde ederiz. D = 16 – 12 = 4 a 1 = 1 a 2 = 1 / 3 Orijinal değişkene dönelim: │ x│=1 ve │х│= 1/3. Her denklemin iki kökü vardır. Cevap: x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Denklemi çözün: 5x 2 + 3│x│- 1 = 1 / 2 │x│ + 3x 2

Popülasyonun ilk sisteminin çözümünü bulalım: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 x 2'nin sağlamadığına dikkat edin x ≥ 0 koşulu. Çözüm ikinci sistemin sayısı olacaktır, zıt anlam x 1. Cevap: x 1 = -5+√57 / 8 ; X 2 = 5-√57 / 8 .№3 . Denklemi çözün: x 4 – │х│= 0 │х│= a'yı gösterelim, burada a ≥ 0. a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 denklemini elde ederiz. a 2 = 1 Orijinal değişkene dönün: │х│=0 ve │х│= 1 x = 0; ± 1 Cevap: x 1 = 0; X 2 = 1; X 3 = - 1.
Egzersizler: №6. Denklemi çözün: 2│х│ - 4,5 = 5 – 3 / 8 │х│ №7 . Denklemi çözün, cevabınızdaki kök sayısını belirtin: 3x 2 - 7│x│ + 2 = 0 №8 . Denklemi çözün, cevabınızda tamsayı çözümleri belirtin: x 4 + │x│ - 2 = 0

Bölüm 3. │F(x)│ = G(x) formundaki denklemler

Bu tür bir denklemin sağ tarafı bir değişkene bağlıdır ve bu nedenle ancak ve ancak sağ tarafın bir G(x) ≥ 0 fonksiyonu olması durumunda bir çözümü vardır. Orijinal denklem iki şekilde çözülebilir : 1 yol: Standart, tanımına dayalı bir modülün açıklanmasına dayalıdır ve iki sistemin birleşimine eşdeğer bir geçişten oluşur. │ F(x)│ =G(X)

Bu yöntem şu durumlarda rasyonel olarak kullanılabilir: karmaşık ifade G(x) fonksiyonu için ve daha az karmaşık olan – F(x) fonksiyonu için, çünkü eşitsizliklerin F(x) fonksiyonu ile çözüldüğü varsayılmaktadır. Yöntem 2: Sağ tarafa bir koşulun uygulandığı eşdeğer bir sisteme geçişten oluşur. │ F(X)│= G(X)

G(x) fonksiyonuna ilişkin ifade, F(x) fonksiyonuna göre daha az karmaşıksa bu yöntemin kullanılması daha uygundur, çünkü G(x) eşitsizliğinin çözümü ≥ 0 olarak kabul edilir. birden fazla modülden ikinci seçeneğin kullanılması önerilir. Örnekler: №1. Denklemi çözün: │x + 2│= 6 -2x

(1 yollu) Cevap: x = 1 1 / 3 №2.
│x 2 – 2x - 1│= 2 (x + 1)

(2 yol) Cevap: Köklerin çarpımı 3'tür.
№3. Denklemi çözün ve cevabınızdaki köklerin toplamını belirtin:
│x - 6│= x 2 - 5x + 9

Cevap: Köklerin toplamı 4'tür.
Egzersizler: №9. │x + 4│= - 3x №10. Denklemi çözün, cevabınızdaki çözüm sayısını belirtin:│x 2 + x - 1│= 2x – 1 №11 . Denklemi çözün, cevabınızda köklerin çarpımını belirtin:│x + 3│= x 2 + x – 6

Bölüm 4. │F(x)│= F(x) ve │F(x)│= - F(x) formunun denklemleri

Bu tür denklemlere bazen "en güzel" denir. Denklemlerin sağ tarafı değişkene bağlı olduğundan, çözümler ancak ve ancak sağ tarafın negatif olmaması durumunda mevcuttur. Bu nedenle orijinal denklemler eşitsizliklere eşdeğerdir:
│F(x)│= F(x) F(x) ≥ 0 ve │F(x)│= - F(x) F(x) Örnekler: №1 . Denklemi çözün, cevabınızdaki tam kökün küçüğünü belirtin: │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Cevap: x = 1№2. Denklemi çözün, aralığın uzunluğunu cevabınızda belirtin: │х 2 - 9│= 9 – x 2 x 2 – 9 ≤ 0 (x – 3) (x + 3) ≤ 0 [- 3; 3] Cevap: Boşluğun uzunluğu 6'dır.№3 . Denklemi çözün ve cevabınızdaki tam sayı çözümlerin sayısını belirtin: │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1; 2] Cevap: 4 tam çözüm.№4 . Denklemi çözün ve cevabınızda belirtin en büyük kök:
│4 – x -

│= 4 – x –

x 2 – 5x + 5 = 0 D = 5 x 1,2 =

≈ 1,4

Cevap: x = 3.

Egzersizler: №12. Denklemi çözün, cevabınızda kökün tamamını belirtin: │x 2 + 6x + 8│= x 2 + 6x + 8 №13. Denklemi çözün, cevabınızdaki tamsayı çözümlerin sayısını belirtin: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14. Denklemi çözün; cevabınızda denklemin kökü olmayan bir tamsayıyı belirtin:

Bölüm 5. │F(x)│= │G(x)│ formundaki denklemler

Denklemin her iki tarafı da negatif olmadığından çözüm iki durumu dikkate almayı içerir: alt modüler ifadeler eşit veya zıt işaretlidir. Bu nedenle orijinal denklem iki denklemin birleşimine eşdeğerdir: │ F(X)│= │ G(X)│

Örnekler: №1. Denklemi çözün, cevabınızda kökün tamamını belirtin: │x + 3│=│2x - 1│

Cevap: Tam kök x = 4.№2. Denklemi çözün: │ x – x 2 - 1│=│2x – 3 – x 2 │

Cevap: x = 2.№3 . Denklemi çözün ve cevabınızda köklerin çarpımını belirtin:

Kök denklemler 4x 2 + 2x – 1 = 0 x 1,2 = - 1±√5 / 4 Cevap: Köklerin çarpımı – 0,25’tir. Egzersizler: №15 . Denklemi çözün ve cevabınızda çözümün tamamını belirtin: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16. Denklemi çözün, cevabınızdaki kökün küçük olanını belirtin:│5x - 3│=│7 - x│ №17 . Denklemi çözün ve cevabınızdaki köklerin toplamını belirtin:

Bölüm 6. Standart olmayan denklemlerin çözümüne örnekler

İÇİNDE bu bölümİfadenin mutlak değerinin tanım gereği ortaya çıktığını çözerken standart olmayan denklem örneklerini ele alacağız. Örnekler:

№1. Denklemi çözün, cevabınızdaki köklerin toplamını belirtin: x · │x│- 5x – 6 = 0
Cevap: Köklerin toplamı 1'dir №2. . Denklemi çözün, cevabınızdaki kökün küçük olanını belirtin: x 2 - 4x ·
- 5 = 0
Cevap: daha küçük kök x = - 5. №3. Denklemi çözün:

Cevap: x = -1. Egzersizler: №18. Denklemi çözün ve köklerin toplamını belirtin: x · │3x + 5│= 3x 2 + 4x + 3
№19. Denklemi çözün: x 2 – 3x =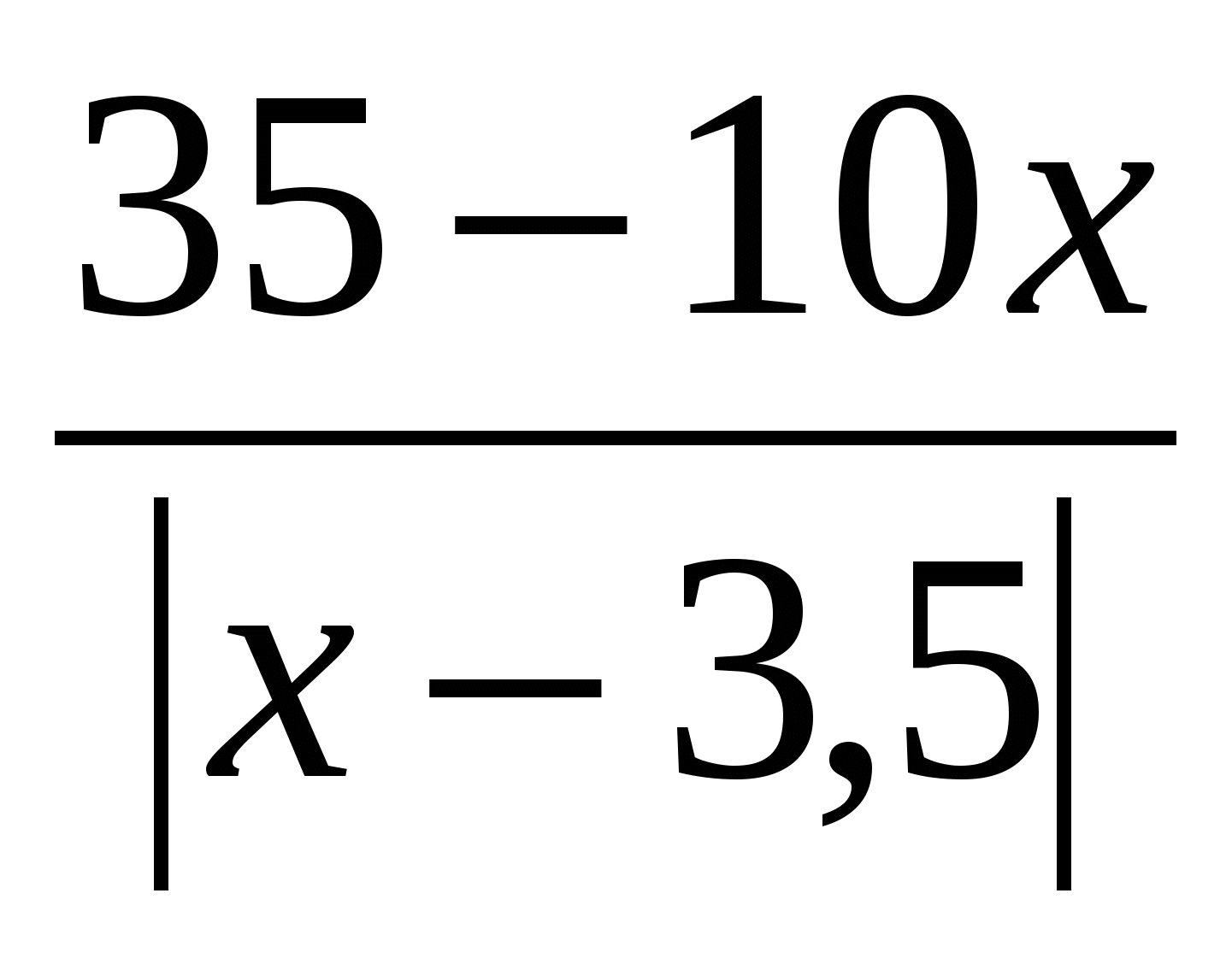

№20. Denklemi çözün:

Bölüm 7. │F(x)│+│G(x)│=0 formundaki denklemler

Bu tür denklemin sol tarafında negatif olmayan miktarların toplamının bulunduğunu fark etmek kolaydır. Bu nedenle, orijinal denklemin bir çözümü ancak ve ancak her iki terimin de aynı anda sıfıra eşit olması durumunda vardır. Denklem denklem sistemine eşdeğerdir: │ F(X)│+│ G(X)│=0
Örnekler: №1 . Denklemi çözün:

Cevap: x = 2. №2. Denklemi çözün: Cevap: x = 1. Egzersizler: №21. Denklemi çözün: №22 . Denklemi çözün ve cevabınızdaki köklerin toplamını belirtin: №23 . Denklemi çözün ve cevabınızdaki çözüm sayısını belirtin:

Bölüm 8. │a 1 x + b 1 │±│a 2 x + b 2 │± … │a n x +b n │= m formundaki denklemler

Bu tür denklemleri çözmek için aralık yöntemi kullanılır. Bunu modüllerin sıralı genişletilmesiyle çözersek, şunu elde ederiz: Nçok hantal ve elverişsiz olan sistem setleri. Aralık yöntemi algoritmasını ele alalım: 1). Değişken değerlerini bulun X, burada her modül sıfıra eşit(alt modüler ifadelerin sıfırları):

2). Bulunan değerleri aralıklara bölünmüş bir sayı doğrusu üzerinde işaretleyin (aralık sayısı sırasıyla eşittir) N+1 ) 3). Ortaya çıkan aralıkların her birinde her modülün hangi işaretle ortaya çıktığını belirleyin (bir çözüm formüle ederken, üzerindeki işaretleri işaretleyerek bir sayı doğrusu kullanabilirsiniz) 4). Orijinal denklem toplama eşdeğerdir N+1 Her birinde değişkenin üyeliğinin belirtildiği sistemler X aralıklardan biridir. Örnekler: №1 . Denklemi çözün ve cevabınızdaki en büyük kökü belirtin:

1). Alt modüler ifadelerin sıfırlarını bulalım: x = 2; x = -3 2). Bulunan değerleri sayı doğrusu üzerinde işaretleyelim ve ortaya çıkan aralıklarda her modülün hangi işaretle ortaya çıktığını belirleyelim:
x – 2 x – 2 x – 2 - - + - 3 2x2x + 6 2x + 6 2x + 6 - + + 3)

- çözüm yok Denklemin iki kökü var. Cevap: En büyük kök x = 2. №2. Denklemi çözün ve cevabınızda kökün tamamını belirtin:

1). Alt modüler ifadelerin sıfırlarını bulalım: x = 1,5; x = - 1 2). Bulunan değerleri sayı doğrusu üzerinde işaretleyelim ve ortaya çıkan aralıklarda her modülün hangi işaretle ortaya çıktığını belirleyelim: x + 1 x + 1 x + 1 - + +
-1 1,5 x 2x – 3 2x – 3 2x – 3 - - +
3).

En son sistemçözümü yoktur, dolayısıyla denklemin iki kökü vardır. Denklemi çözerken ikinci modülün önündeki “-” işaretine dikkat etmelisiniz. Cevap: Tam kök x = 7. №3. Denklemi çözün, cevabınızda köklerin toplamını belirtin: 1). Alt modüler ifadelerin sıfırlarını bulalım: x = 5; x = 1; x = - 2 2). Bulunan değerleri sayı doğrusu üzerinde işaretleyelim ve ortaya çıkan aralıklarda her modülün hangi işaretle ortaya çıktığını belirleyelim: x – 5 x – 5 x – 5 x – 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).

Denklemin x = 0 ve 2 olmak üzere iki kökü vardır. Cevap: Köklerin toplamı 2'dir. №4 . Denklemi çözün: 1). Alt modüler ifadelerin sıfırlarını bulalım: x = 1; x = 2; x = 3.2). Ortaya çıkan aralıklarda her modülün hangi işaretle ortaya çıktığını belirleyelim. 3).

İlkinin çözümlerini birleştirelim üç sistem. Cevap: ; x = 5.
Egzersizler: №24. Denklemi çözün:

№25. Denklemi çözün ve cevabınızdaki köklerin toplamını belirtin: №26. Denklemi çözün ve cevabınızdaki daha küçük kökü belirtin: №27. Denklemi çözün ve cevabınızdaki büyük kökü belirtin:

Bölüm 9. Birkaç modül içeren denklemler

Birden fazla modül içeren denklemler, alt modüler ifadelerde mutlak değerlerin varlığını varsayar. Bu tür denklemleri çözmenin temel ilkesi, modüllerin “harici” olandan başlayarak sıralı olarak açıklanmasıdır. Çözüm sırasında 1 No'lu Bölüm 3'te anlatılan teknikler kullanılır.

Örnekler: №1. Denklemi çözün:
Cevap: x = 1; - on bir. №2. Denklemi çözün:
Cevap: x = 0; 4; - 4. №3. Denklemi çözün ve cevabınızda köklerin çarpımını belirtin:
Cevap: Köklerin çarpımı -8'dir. №4. Denklemi çözün:
Nüfus denklemlerini gösterelim (1) Ve (2) ve tasarım kolaylığı için her birinin çözümünü ayrı ayrı düşünün. Her iki denklem de birden fazla modül içerdiğinden sistem kümelerine eşdeğer bir geçiş yapmak daha uygundur. (1)

(2)

Cevap:
Egzersizler: №36. Denklemi çözün, cevabınızdaki köklerin toplamını belirtin: 5 │3x-5│ = 25 x №37. Denklemi çözün, birden fazla kök varsa cevabınızda köklerin toplamını belirtin: │x + 2│ x – 3x – 10 = 1 №38. Denklemi çözün: 3 │2x -4│ = 9 │x│ №39. Denklemi çözün ve cevabınızdaki kök sayısını belirtin: 2 │ sin x│ = √2 №40 . Denklemi çözün ve cevabınızdaki kök sayısını belirtin:

Bölüm 3. Logaritmik denklemler.

Aşağıdaki denklemleri çözmeden önce logaritmanın özelliklerini gözden geçirmek gerekir. logaritmik fonksiyon. Örnekler: №1. Denklemi çözün, cevabınızda köklerin çarpımını belirtin: log 2 (x+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ - 1

Durum 1: x ≥ - 1 ise log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – x ≥ - 1 koşulunu karşılar 2 durum: eğer x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – x - 1 koşulunu karşılıyor
Cevap: Köklerin çarpımı – 15’tir.
№2. Denklemi çözün, cevabınızdaki köklerin toplamını belirtin: lg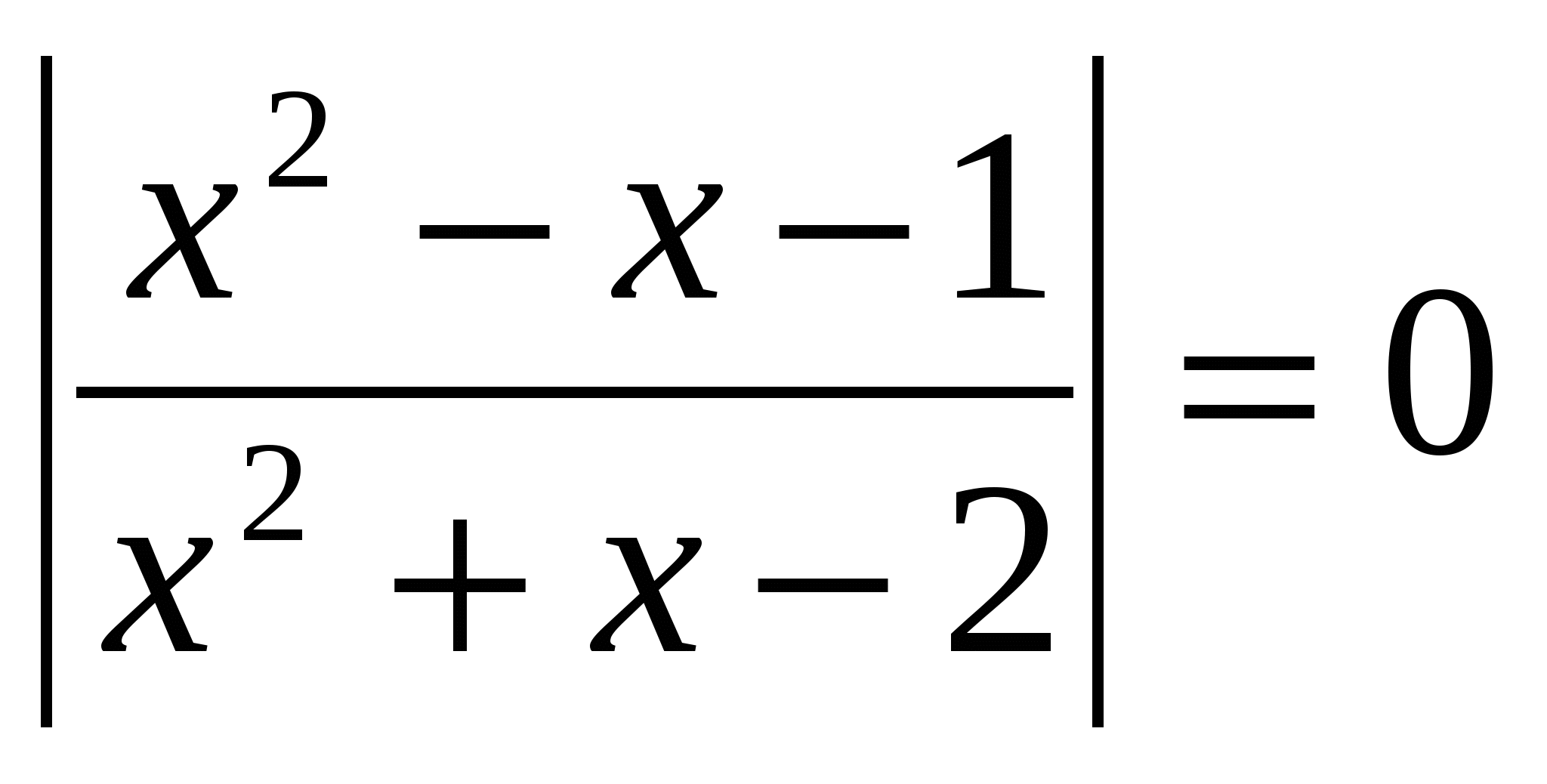
O.D.Z.

Cevap: Köklerin toplamı 0,5'tir.
№3. Denklemi çözün: log 5
O.D.Z.

Cevap: x = 9. №4. Denklemi çözün: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Başka bir tabana geçmek için formülü kullanalım. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Alt modüler ifadelerin sıfırlarını bulalım: x = 25; x = Bu sayılar alanı bölüyor kabul edilebilir değerlerüç aralığa bölündüğüne göre denklem eşdeğerdir üçlü kombinasyon sistemler
Cevap: )