PRAKTINIS DARBAS Nr.1
Tema: "Algebrinės, racionalios, neracionalios, galios išraiškos».
Darbo tikslas: išmokti transformuoti algebrines, racionaliąsias, iracionaliąsias, galios išraiškas naudojant sutrumpintas daugybos formules, pagrindines šaknų ir laipsnių savybes.
Teorinė informacija.
GAMTOS LAIPSNIO ŠAKNYS NUO SKAIČIŲ, JŲ SAVYBĖS.
Šaknis n – laipsnių : , n - šaknies rodiklis, A - radikali išraiška
Jeigu n - nelyginis skaičius, tada išraiška prasminga, kai A
Jeigu n – lyginis skaičius, tada posakis turi prasmę kada
Aritmetinė šaknis:
![]()
Nelyginė neigiamo skaičiaus šaknis:
PAGRINDINĖS ŠAKNŲ SAVYBĖS
Šaknies ištraukimo iš produkto taisyklė:
![]()
Šaknies iš šaknies ištraukimo taisyklė:
![]()
Daugiklio pašalinimo iš po šaknies ženklo taisyklė:
Įvesdami daugiklį po šaknies ženklu:
![]() ,
,
Šaknies indeksą ir radikalios išraiškos indeksą galima padauginti iš to paties skaičiaus.
![]()
Taisyklė, kaip pakelti šaknį į valdžią.
LAIPSNIS SU NATŪRALIU RODIKLIU
= , a – laipsnio pagrindas,n – eksponentas
Savybės:
Dauginant laipsnius su tomis pačiomis bazėmis, eksponentai pridedami, tačiau bazė lieka nepakitusi.
![]()
Dalijant laipsnius su tomis pačiomis bazėmis, rodikliai atimami, tačiau bazė lieka nepakitusi.
![]()
Didinant laipsnį į laipsnį, rodikliai dauginami.
Didinant dviejų skaičių sandaugą iki laipsnio, kiekvienas skaičius didinamas iki to laipsnio ir rezultatai dauginami.
![]()
Jei dviejų skaičių koeficientas padidinamas iki laipsnio, tai skaitiklis ir vardiklis pakeliami iki šios laipsnio, o rezultatas dalijamas vienas iš kito.
LAIPSNIS SU SVEIKIU SKAIČIU RODIKLIU
![]()
Savybės:
adresu r >0 > adresu r <0
7 . Bet kokiems racionaliems skaičiamsr Irs nuo nelygybės > turėtų
> adresu a >1 adresu
Sutrumpintos daugybos formulės.

1 pavyzdys. Supaprastinkite išraišką.
Taikykime galių savybes (padauginkime laipsnius su tuo pačiu pagrindu ir įgaliojimų padalijimas ta pačia baze):  .
.
Atsakymas: 9m 7 .
2 pavyzdys. Sumažinti dalį:
Sprendimas Taigi trupmenos apibrėžimo sritis yra visi skaičiai, išskyrus x ≠ 1 ir x ≠ -2. ![]() .Sumažinę trupmeną gauname .Gautos trupmenos apibrėžimo sritis: x ≠ -2, t.y. platesnis nei pradinės trupmenos apibrėžimo diapazonas. Todėl trupmenos ir yra lygios x ≠ 1 ir x ≠ -2.
.Sumažinę trupmeną gauname .Gautos trupmenos apibrėžimo sritis: x ≠ -2, t.y. platesnis nei pradinės trupmenos apibrėžimo diapazonas. Todėl trupmenos ir yra lygios x ≠ 1 ir x ≠ -2.
3 pavyzdys. Sumažinti dalį: ![]()
4 pavyzdys. Supaprastinti: ![]()
5 pavyzdys.Supaprastinti: ![]()
6 pavyzdys. Supaprastinti: ![]()
7 pavyzdys. Supaprastinti: ![]()
8 pavyzdys. Supaprastinti: 
9 pavyzdys. Apskaičiuokite: ![]() .
.
Sprendimas.
10 pavyzdys. Supaprastinkite išraišką:
Sprendimas. 
11 pavyzdys.Sumažinkite dalį, jei
Sprendimas. ![]() .
.
12 pavyzdys. Išlaisvinkite save nuo neracionalumo trupmenos vardiklyje
Sprendimas. Vardiklyje turime 2-ojo laipsnio neracionalumą, todėl tiek trupmenos skaitiklį, tiek vardiklį dauginame iš konjuguotos išraiškos, tai yra skaičių sumos ir , tada vardiklyje turime kvadratų skirtumą, kuris pašalina neracionalumą.
OPTION - aš1. Supaprastinkite išraišką:



 , kur a yra racionalus skaičius,
b
– natūralusis skaičius
, kur a yra racionalus skaičius,
b
– natūralusis skaičius
 ,
, 
5. Supaprastinkite:
 ;
; 
 ,
,  ,
, 
 10. Atlikite šį veiksmą:
10. Atlikite šį veiksmą:
8. Sumažinkite trupmeną 

9. Imkitės veiksmų 
OPTION - II
1. Supaprastinkite išraišką:

2. Raskite posakio reikšmę:

3. Įsivaizduokite laipsnį su trupmeninis rodiklisšaknies pavidalu

4. Švinas nurodyta išraiškaį protą  , kur a yra racionalus skaičius,
b
– natūralusis skaičius
, kur a yra racionalus skaičius,
b
– natūralusis skaičius
 ,
, 
5. Supaprastinkite:
 ;
; 
6. Pakeiskite aritmetines šaknis laipsniais su trupmeniniu rodikliu
 ,
,  ,
, 
7. Pateikite išraišką kaip trupmeną, kurios vardiklyje nėra šaknies ženklo
 10. Atlikite šį veiksmą:
10. Atlikite šį veiksmą:
8. Sumažinkite trupmeną 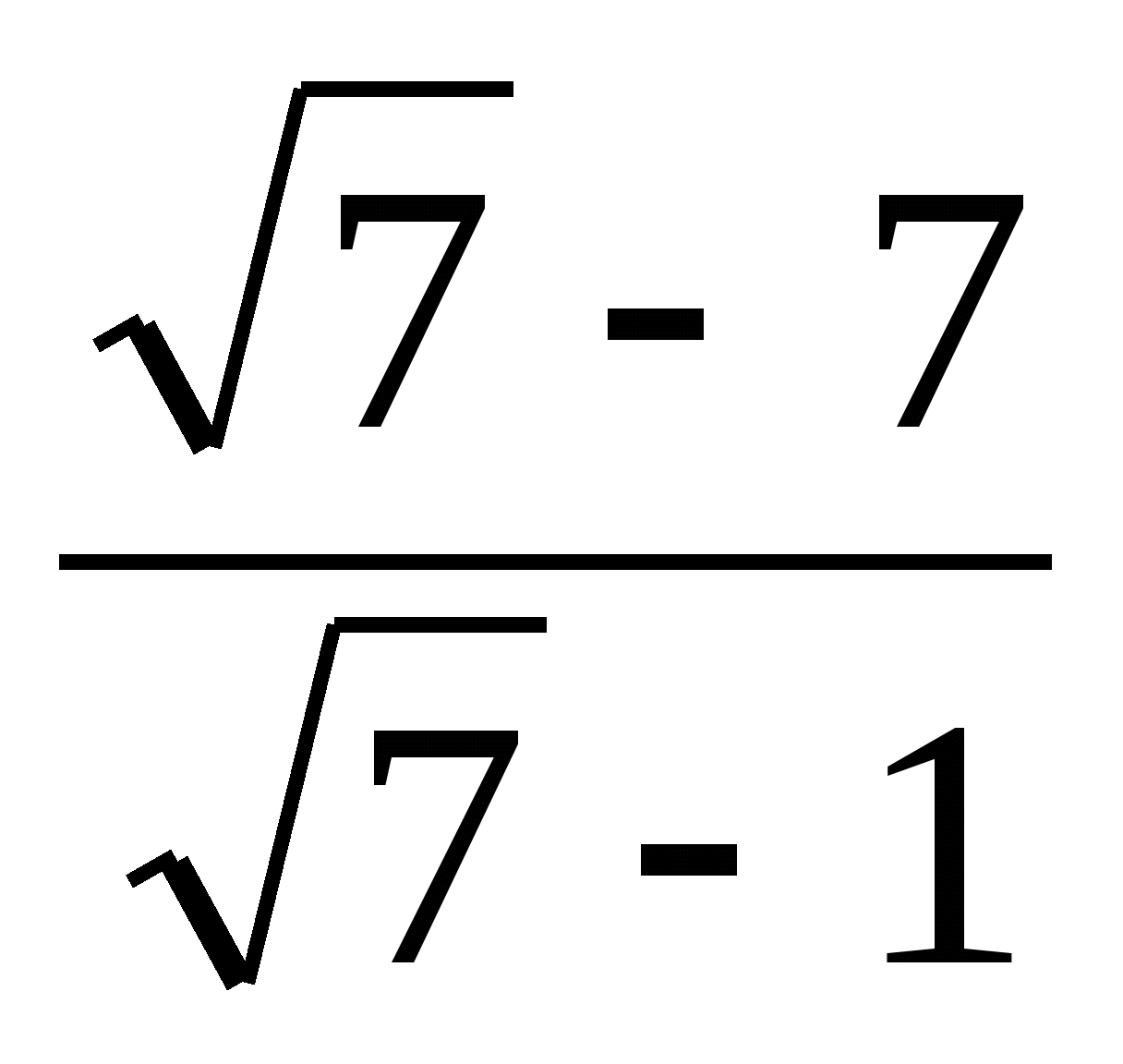

9. Imkitės veiksmų 
1. Atlikite šį veiksmą:

2. Raskite posakio reikšmę:

3. Laipsnį su trupmeniniu laipsniu pavaizduokite kaip šaknį

4. Sumažinkite nurodytą išraišką iki formos  , kur a yra racionalus skaičius,
b
– natūralusis skaičius
, kur a yra racionalus skaičius,
b
– natūralusis skaičius
 ,
, 
5. Supaprastinkite:
 ;
; 
6. Pakeiskite aritmetines šaknis laipsniais su trupmeniniu rodikliu
 ,
,  ,
, 
7. Pateikite išraišką kaip trupmeną, kurios vardiklyje nėra šaknies ženklo
 10. Atlikite šį veiksmą:
10. Atlikite šį veiksmą:
8. Sumažinkite trupmeną 

9. Imkitės veiksmų

OPTION - IV
1. Atlikite šį veiksmą:

2. Raskite posakio reikšmę:

3. Laipsnį su trupmeniniu laipsniu pavaizduokite kaip šaknį

 ,
, 
4. Sumažinkite nurodytą išraišką iki formos  , kur a yra racionalus skaičius,
b
– natūralusis skaičius
, kur a yra racionalus skaičius,
b
– natūralusis skaičius
 ,
, 
5. Supaprastinkite:
Iracionalios išraiškos ir jų transformacijos
Paskutinį kartą prisiminėme (arba sužinojome, priklausomai nuo to), kas tai yra , išmoko išgauti tokias šaknis, po gabalo išsiaiškino pagrindines šaknų savybes ir nusprendė ne sudėtingų pavyzdžių su šaknimis.
Ši pamoka bus ankstesnės tęsinys ir bus skirta daugumos transformacijai skirtingos išraiškos turinčios visų rūšių šaknis. Tokios išraiškos vadinamos neracionalus. Čia atsiras išraiškos su raidėmis, papildomos sąlygos, neracionalumo pašalinimas trupmenomis ir keletas pažangių darbo su šaknimis technikų. Technikai, kurios bus aptartos šią pamoką, bus geras pagrindas spręsti Vieningo valstybinio egzamino problemos(ir ne tik) beveik bet kokio sudėtingumo. Taigi pradėkime.
Pirmiausia pakartosiu čia pagrindinės formulės ir šaknų savybės. Kad nešokinėtum iš temos į temą. Štai jie:
![]()
![]() adresu
adresu
![]()
Jūs turite žinoti šias formules ir mokėti jas taikyti. Ir į abi puses – tiek iš kairės į dešinę, tiek iš dešinės į kairę. Būtent jomis grindžiamas daugelio bet kokio sudėtingumo užduočių sprendimas. Pradėkime nuo kol kas paprasčiausio dalyko – nuo tiesioginis taikymas formules ar jų derinius.
Lengvas formulių pritaikymas
Šioje dalyje bus nagrinėjami paprasti ir nekenksmingi pavyzdžiai – be raidžių, papildomų sąlygų ir kitų gudrybių. Tačiau net ir juose, kaip taisyklė, yra galimybių. Ir kuo įmantresnis pavyzdys, tuo daugiau tokių variantų. O nepatyręs studentas turi pagrindinė problema– nuo ko pradėti? Atsakymas čia paprastas - Jei nežinai, ko tau reikia, daryk, ką gali. Kol jūsų veiksmai yra taikoje ir dera su matematikos taisyklėmis ir joms neprieštarauja.) Pavyzdžiui, ši užduotis:
Apskaičiuokite:
Net ir tokiame paprastame pavyzdyje yra keli galimi atsakymo keliai.
Pirmasis yra tiesiog padauginti šaknis iš pirmosios savybės ir išgauti šaknį iš rezultato:
Antrasis variantas yra toks: mes jo neliečiame, dirbame su . Išimame faktorių iš po šaknies ženklo, o tada – pagal pirmąją savybę. kaip tai:
Galite nuspręsti tiek, kiek norite. Bet kuriame iš variantų atsakymas yra vienas - aštuoni. Pavyzdžiui, man lengviau padauginti iš 4 ir 128 ir gauti 512, o kubo šaknį galima lengvai išgauti iš šio skaičiaus. Jei kas nors neprisimena, kad 512 yra 8 kubeliai, tai nesvarbu: galite parašyti 512 kaip 2 9 (pirmosios 10 dviejų laipsnių, tikiuosi pamenate?) ir naudodami laipsnio šaknies formulę :
Kitas pavyzdys.
Apskaičiuokite:.
Jei dirbsi pagal pirmą savybę (viską padėdamas po viena šaknimi), gausi nemenką skaičių, iš kurio paskui bus galima ištraukti šaknį – taip pat ne cukrų. Ir tai nėra faktas, kad jis bus išgautas tiksliai.) Todėl čia naudinga pašalinti veiksnius iš skaičiaus šaknies. Ir išnaudokite visas galimybes:
O dabar viskas gerai:
Belieka po viena šaknimi įrašyti aštuonis ir du (pagal pirmąją savybę) ir darbas atliktas. :)
Dabar pridėkime keletą trupmenų.
Apskaičiuokite:
Pavyzdys gana primityvus, bet turi ir galimybių. Galite naudoti daugiklį, norėdami transformuoti skaitiklį ir sumažinti jį vardikliu:

Arba galite iš karto naudoti šaknų padalijimo formulę:

Kaip matome, taip ir taip yra teisinga.) Jei nesuklupsi pusiaukelėje ir nesuklysi. Nors kur man čia suklysti...
Dabar pažvelkime į labiausiai paskutinis pavyzdys iš namų darbai paskutinė pamoka:
Supaprastinti:
![]()
Visiškai neįsivaizduojamas šaknų rinkinys ir netgi įdėtos. Ką turėčiau daryti? Svarbiausia nebijoti! Čia pirmiausia po šaknimis pastebime skaičius 2, 4 ir 32 – dviejų laipsnius. Pirmiausia reikia sumažinti visus skaičius iki dviejų: juk tuo daugiau identiški skaičiai pavyzdyje kuo mažiau skirtingų, tuo paprasčiau.) Pradėkime atskirai nuo pirmojo veiksnio:
![]()
Skaičius gali būti supaprastintas sumažinus du po šaknimi su keturiais šaknies eksponente:
Dabar, atsižvelgiant į darbo šaknį:
![]() .
.
Skaičiuje išimame du kaip šaknies ženklą:
Ir mes susiduriame su išraiška naudodami šaknies formulės šaknį:
Taigi pirmasis veiksnys bus parašytas taip:
Likusios šaknys išnyko, skaičiai sumažėjo, tai jau džiugina. Tiesiog šaknys skirtingos, bet kol kas taip ir paliksime. Esant poreikiui juos konvertuosime į tokius pat. Paimkime antrąjį veiksnį.)
Antrąjį faktorių transformuojame panašiai, naudodami sandaugos šaknies ir šaknies šaknies formulę. Jei reikia, sumažiname rodiklius naudodami penktąją formulę:
Viską įdedame į originalus pavyzdys ir gauname:
Gavome visą krūvą visiškai skirtingų šaknų produktą. Būtų gerai juos visus suvesti į vieną rodiklį, o tada pamatysime. Na, tai visai įmanoma. Didžiausias iš šaknies rodiklių yra 12, o visi kiti - 2, 3, 4, 6 - yra skaičiaus 12 dalikliai. Todėl visas šaknis pagal penktąją savybę sumažinsime iki vieno eksponento - 12:
![]()
Suskaičiuojame ir gauname:
Mes negavome gražaus skaičiaus, bet tai gerai. Mūsų paklausė supaprastinti išraiška, ne skaičiuoti. Supaprastinta? tikrai! Ir atsakymo tipas (sveikasis skaičius ar ne) čia nebevaidina jokio vaidmens.
Kai kurios sudėjimo/atimties ir sutrumpintos daugybos formulės
Deja, bendrosios formulės Už šaknų pridėjimas ir atėmimas ne matematikoje. Tačiau užduotyse šie veiksmai su šaknimis dažnai aptinkami. Čia reikia suprasti, kad bet kokios šaknys yra lygiai tokie pat matematiniai simboliai, kaip ir raidės algebroje.) O šaknims galioja ta pati technika ir taisyklės kaip ir raidėms – skliaustų atidarymas, panašių atvedimas, sutrumpintos daugybos formulės ir pan.
Pavyzdžiui, visiems aišku, kad . Lygiai taip pat identiškasŠaknis galima gana lengvai pridėti/atimti viena nuo kitos:
![]()
![]()
Jei šaknys skirtingos, tuomet ieškome būdo, kaip jas padaryti vienodas – pridedant/atimant daugiklį arba naudojant penktąją savybę. Jei tai niekaip nesupaprastinta, tai galbūt transformacijos yra gudresnės.
Pažiūrėkime į pirmąjį pavyzdį.
Raskite posakio reikšmę: .
Visos trys šaknys, nors ir kubinės, yra iš skirtinga skaičių. Jie nėra grynai išgaunami ir pridedami / atimami vienas iš kito. Todėl bendrųjų formulių naudojimas čia netinka. Ką turėčiau daryti? Išimkime kiekvienos šaknies veiksnius. Bet kokiu atveju blogiau nebus.) Be to, iš tikrųjų nėra kitų galimybių:
Todėl,.
Štai ir sprendimas. Čia su pagalba perėjome nuo skirtingų šaknų prie tų pačių daugiklio pašalinimas iš po šaknies. O paskui tiesiog atnešė panašių.) Nusprendžiame toliau.
Raskite išraiškos reikšmę:
Tikrai nieko nepadarysi dėl septyniolikos šaknies. Dirbame pagal pirmąją savybę - iš dviejų šaknų sandaugos darome vieną šaknį:
Dabar pažiūrėkime atidžiau. Ką mes turime po didžiuoju kubo šaknis? Skirtumas yra nedidelis... Na, žinoma! Kvadratų skirtumas:
Dabar belieka išgauti šaknį: .
Apskaičiuokite:
Čia turėsite parodyti matematinį išradingumą.) Mes galvojame maždaug taip: „Taigi, pavyzdyje – šaknų produktas. Po viena šaknimi yra skirtumas, o po kita - suma. Labai panaši į kvadratų formulę. Bet... Šaknys kitokios! Pirmoji – kvadratinė, o antroji – ketvirto laipsnio... Būtų gerai, kad jos būtų vienodos. Pagal penktąją savybę galima nesunkiai kvadratinė šaknis padaryti ketvirtą šaknį. Norėdami tai padaryti, užtenka išlyginti radikalią išraišką.
Jei galvojote apie tą patį, tada esate pusiaukelėje į sėkmę. Visiškai teisingai! Pirmąjį veiksnį paverskime ketvirtąja šaknimi. kaip tai:
![]()
Dabar nieko nereikia daryti, bet turėsite prisiminti skirtumo kvadrato formulę. Tik tepant ant šaknų. Taigi ką? Kodėl šaknys yra blogesnės už kitus skaičius ar išraiškas?! Mes statome:
„Hm, na, jie jį pastatė, o kas? Krienai nėra saldesni už ridikus. Sustok! O jei išimsi keturis po šaknimi? Tada atsiras ta pati išraiška, kaip ir po antrąja šaknimi, tik su minusu, o mes būtent tai ir siekiame!
Teisingai! Paimkime keturis:
![]() .
.
O dabar – technologijos reikalas:
Taip išpainiojami sudėtingi pavyzdžiai.) Dabar laikas praktikuoti su trupmenomis.
Apskaičiuokite:
Aišku, kad skaitiklį reikia konvertuoti. Kaip? Žinoma, naudojant sumos kvadrato formulę. Ar turime kitų galimybių? :) Padalijame kvadratu, išimame faktorius, mažiname rodiklius (kur reikia):
Oho! Gavome tiksliai savo trupmenos vardiklį.) Tai reiškia, kad visa trupmena akivaizdžiai lygi vienetui:

Kitas pavyzdys. Tik dabar kita sutrumpinto daugybos formulė.)
Apskaičiuokite:
Akivaizdu, kad skirtumo kvadratas turi būti naudojamas praktiškai. Atskirai išrašome vardiklį ir – einam!
Iš po šaknų išimame veiksnius:
![]()
Vadinasi,
Dabar viskas, kas bloga, yra labai sumažinta ir pasirodo:

Na, perkelkime tai į kitą lygį. :)
Laiškai ir papildomos sąlygos
Pažodiniai posakiai su šaknimis yra sudėtingesnis dalykas nei skaitinės išraiškos, ir yra neišsenkantis šaltinis erzinančių ir labai rimtų klaidų. Uždarykite šį šaltinį.) Klaidos kyla dėl to, kad tokiose užduotyse dažnai naudojami neigiami skaičiai ir išraiškos. Jie mums pateikiami tiesiogiai atliekant užduotį arba paslėpti laiškus ir papildomas sąlygas. O dirbdami su šaknimis turime nuolat tai atsiminti šaknyse lygus laipsnis tiek po pačia šaknimi, tiek dėl šaknų ištraukimo turėtų būti neneigiama išraiška. Pagrindinė šios pastraipos užduočių formulė bus ketvirtoji formulė:
Su šaknimis nelyginis laipsnis Klausimų nekyla – ten visada išgaunama viskas, tiek pliusas, tiek minusas. O minusas, jei ką, iškeliamas į priekį. Eikime tiesiai prie šaknų net laipsnių.) Pavyzdžiui, tokia trumpa užduotis.
Supaprastinti: , Jeigu .
Atrodytų, viskas paprasta. Tai tiesiog pasirodys X.) Bet kodėl tada papildoma sąlyga ? Tokiais atvejais pravartu įvertinti skaičiais. Grynai dėl savęs.) Jeigu, tada x yra akivaizdžiai neigiamas skaičius. Pavyzdžiui, minus trys. Arba minus keturiasdešimt. Tegul . Ar galite padidinti minus tris iki ketvirtos laipsnio? tikrai! Rezultatas yra 81. Ar įmanoma išgauti ketvirtą šaknį iš 81? Kodėl gi ne? Gali! Gauni tris. Dabar išanalizuokime visą mūsų grandinę:
Ką mes matome? Įvestis buvo neigiamas skaičius, o išvestis jau buvo teigiama. Buvo minus trys, dabar plius trys.) Grįžkime prie raidžių. Be jokios abejonės, modulo tai bus tiksliai x, bet tik pats x yra minusas (pagal sąlygą!), o ištraukimo rezultatas (pagal aritmetinė šaknis!) turi būti pliusas. Kaip gauti pliusą? Labai paprasta! Norėdami tai padaryti, užtenka prieš akivaizdžiai neigiamą skaičių įdėti minusą.) Ir teisingas sprendimas atrodo taip:
Beje, jei naudotume formulę, tai prisiminę modulio apibrėžimą iškart gautume teisingą atsakymą. Kadangi
|x| = -x ties x<0.
Išimkite faktorių iš šaknies ženklo: , Kur .
Pirmas žvilgsnis yra radikali išraiška. Viskas čia gerai. Bet kokiu atveju jis bus neneigiamas. Pradėkime išgauti. Naudodami produkto šaknies formulę, išskiriame kiekvieno veiksnio šaknį:
Nemanau, kad reikia aiškinti, iš kur atsirado moduliai.) Dabar išanalizuokime kiekvieną modulį.
Daugiklis | a | paliekame nepakeistą: laiškui neturime jokių sąlygųa. Mes nežinome, ar tai teigiama, ar neigiama. Kitas modulis |b 2 | galima drąsiai praleisti: bet kuriuo atveju išraiškab 2 neneigiamas. Bet apie |c 3 | - čia jau yra problema.) Jei, tada c 3 <0. Стало быть, модуль надо раскрыть su minusu: | c 3 | = - c 3 . Apskritai teisingas sprendimas būtų:
O dabar – atvirkštinė problema. Ne pati lengviausia, iš karto perspėju!
Įveskite daugiklį po šaknies ženklu: .
Jei tučtuojau užrašysite sprendimą taip
tada tu pateko į spąstus. Tai neteisingas sprendimas! Kas atsitiko?
Pažvelkime atidžiau į posakį po šaknimi. Po ketvirtosios galios šaknimi, kaip žinome, turėtų būti neneigiamas išraiška. Priešingu atveju šaknis neturi reikšmės.) Todėl O tai, savo ruožtu, reiškia, kad ir, vadinasi, pati taip pat yra neteigiama: .
Ir čia klaida ta, kad mes pristatome iš esmės ne teigiamas numerį: ketvirtas laipsnis paverčia jį neneigiamas ir gaunamas neteisingas rezultatas - kairėje yra sąmoningas minusas, o dešinėje jau pliusas. Ir įdėkite jį į šaknį net laipsnį mes turime tik teisę neneigiamas skaičiai ar išraiškos. Ir palikite minusą, jei toks yra, prieš šaknį.) Kaip galime pasirinkti ne neigiamą skaičiaus veiksnį, žinant, kad jis pats yra visiškai neigiamas? Taip, lygiai tas pats! Įdėkite minusą.) Ir kad niekas nepasikeistų, kompensuokite tai dar vienu minusu. kaip tai:
![]()
Ir jau dabar neneigiamas Ramiai įvedame skaičių (-b) po šaknimi pagal visas taisykles:
Šis pavyzdys aiškiai parodo, kad, skirtingai nei kitose matematikos šakose, šaknyse teisingas atsakymas ne visada išplaukia iš formulių. Turite pagalvoti ir asmeniškai priimti teisingą sprendimą.) Turėtumėte būti ypač atsargūs prisijungdami neracionalios lygtys ir nelygybės.
Pažvelkime į kitą svarbią techniką dirbant su šaknimis - atsikratyti iracionalumo.
Iracionalumo pašalinimas trupmenomis
Jei posakyje yra šaknų, tai, priminsiu, tokia išraiška vadinama išraiška su neracionalumu. Kai kuriais atvejais gali būti naudinga atsikratyti šio neracionalumo (t. y. šaknų). Kaip galite pašalinti šaknį? Mūsų šaknis išnyksta, kai... pakeliama į galią. Su indikatoriumi, lygiu šaknies indikatoriui arba jo kartotiniu. Bet jei šaknį pakelsime į laipsnį (ty šaknį padauginsime iš pačios reikiamą skaičių kartų), išraiška pasikeis. Negerai.) Tačiau matematikoje yra temų, kur daugyba gana neskausminga. Pavyzdžiui, trupmenomis. Pagal pagrindinę trupmenos savybę, skaitiklį ir vardiklį padauginus (padalijus) iš to paties skaičiaus, trupmenos reikšmė nepasikeis.
Tarkime, kad mums duota ši trupmena:
Ar galima atsikratyti šaknies vardiklyje? Gali! Norėdami tai padaryti, šaknis reikia supjaustyti kubeliais. Ko mums trūksta viso kubo vardiklyje? Mums trūksta daugiklio, t.y.. Taigi trupmenos skaitiklį ir vardiklį padauginame iš

Vardiklio šaknis dingo. Bet... jis pasirodė skaitiklyje. Nieko nepadarysi, toks likimas.) Mums tai nebesvarbu: buvo paprašyta išlaisvinti vardiklį iš šaknų. Išleistas? Be jokios abejonės.)
Beje, tie, kurie jau yra susipažinę su trigonometrija, galėjo atkreipti dėmesį į tai, kad, pavyzdžiui, kai kuriuose vadovėliuose ir lentelėse jie žymimi skirtingai: kažkur , o kažkur . Kyla klausimas – kas teisinga? Atsakymas: viskas teisinga!) Jei atspėsite– tai tiesiog išsivadavimo iš iracionalumo trupmenos vardiklyje rezultatas. :)
Kodėl turėtume išsivaduoti nuo neracionalumo trupmenomis? Koks skirtumas – šaknis yra skaitiklyje ar vardiklyje? Skaičiuoklė vis tiek viską suskaičiuos.) Na, o tiems, kurie nesiskiria su skaičiuokle, tai tikrai praktiškai jokio skirtumo... Bet net ir skaičiuojant skaičiuotuvu galima atkreipti dėmesį į tai, kad padalintiįjungta visa numeris visada yra patogesnis ir greitesnis nei įjungtas neracionalus. Ir aš nutylėsiu apie padalijimą į koloną.)
Šis pavyzdys tik patvirtins mano žodžius.
Kaip čia galime pašalinti vardiklio kvadratinę šaknį? Jei skaitiklis ir vardiklis padauginami iš išraiškos, vardiklis bus sumos kvadratas. Pirmojo ir antrojo skaičių kvadratų suma duos mums tik skaičius be šaknų, o tai labai džiugina. Tačiau... jis pasirodys dvigubas produktas nuo pirmojo skaičiaus iki antrojo, kur vis tiek išliks trijų šaknis. Jis nekanalizuoja. Ką turėčiau daryti? Prisiminkite dar vieną nuostabią sutrumpinto daugybos formulę! Kur nėra dvigubų gaminių, o tik kvadratai:
Išraiška, kurią padauginus iš kokios nors sumos (arba skirtumo), gaunama kvadratų skirtumas, taip pat vadinamas konjuguota išraiška. Mūsų pavyzdyje konjuguota išraiška bus skirtumas. Taigi skaitiklį ir vardiklį padauginame iš šio skirtumo:
Ką aš galiu pasakyti? Dėl mūsų manipuliacijų ne tik dingo vardiklio šaknis, bet ir visai išnyko trupmena! :) Net ir su skaičiuotuvu atimti trijų šaknį iš trijų yra lengviau nei skaičiuoti trupmeną, kai vardiklyje yra šaknis. Kitas pavyzdys.
Išlaisvinkite save nuo neracionalumo trupmenos vardiklyje:
Kaip iš to ištrūkti? Sutrumpinto daugybos su kvadratais formulės neveikia iš karto - visiškai pašalinti šaknų nepavyks dėl to, kad šį kartą mūsų šaknis yra ne kvadratas, o kub. Būtina, kad šaknis kažkaip būtų pakelta į kubą. Todėl reikia naudoti vieną iš formulių su kubeliais. Kurią? Pagalvokime apie tai. Vardiklis yra suma. Kaip galime pasiekti šaknies kubą? Padauginti iš dalinis kvadratinis skirtumas! Taigi, mes pritaikysime formulę kubelių suma. Šis:
Kaip a mes turime tris, ir kaip kokybė b– penkių kubo šaknis:
Ir vėl trupmena dingo.) Tokių situacijų, kai, išsivadavus iš iracionalumo trupmenos vardiklyje, pati trupmena visiškai išnyksta kartu su šaknimis, pasitaiko labai dažnai. Kaip jums patinka šis pavyzdys!
Apskaičiuokite:
![]()
Tiesiog pabandykite pridėti šias tris trupmenas! Jokių klaidų! :) Vieno bendro vardiklio verta. O kas, jei pabandytume išsivaduoti nuo neracionalumo kiekvienos trupmenos vardiklyje? Na, pabandykime:
Oho, kaip įdomu! Visos frakcijos dingo! Visiškai. O dabar pavyzdį galima išspręsti dviem būdais:
Paprasta ir elegantiška. Ir be ilgų ir varginančių skaičiavimų. :)
Štai kodėl išsivadavimo iš iracionalumo operaciją reikia mokėti atlikti trupmenomis. Tokiuose sudėtinguose pavyzdžiuose tai vienintelis dalykas, kuris gelbsti, taip.) Žinoma, niekas neatšaukė dėmesingumo. Yra užduočių, kuriose jūsų prašoma atsikratyti neracionalumo skaitiklis. Šios užduotys niekuo nesiskiria nuo aptartų, tik skaitiklis pašalinamas iš šaknų.)
Sudėtingesni pavyzdžiai
Belieka apsvarstyti keletą specialių darbo su šaknimis technikų ir praktikuoti ne pačius paprasčiausius pavyzdžius. Ir tada gautos informacijos pakaks bet kokio sudėtingumo užduotims išspręsti. Taigi – pirmyn.) Pirmiausia išsiaiškinkime, ką daryti su įdėtomis šaknimis, kai šaknies formulė neveikia. Pavyzdžiui, čia yra pavyzdys.
Apskaičiuokite:
Šaknis yra po šaknimi... Be to, po šaknimis yra suma arba skirtumas. Todėl šaknies šaknies formulė (su eksponentų daugyba) yra čia neveikia. Taigi reikia kažką daryti radikalios išraiškos: Mes tiesiog neturime kitų galimybių. Tokiais pavyzdžiais dažniausiai užšifruojama didelė šaknis tobulas kvadratas tam tikra suma. Arba skirtumai. O aikštės šaknis jau puikiai ištraukta! O dabar mūsų užduotis yra jį iššifruoti.) Toks iššifravimas gražiai atliktas lygčių sistema. Dabar viską pamatysite patys.)
Taigi, po pirmąja šaknimi turime šią išraišką:
Ką daryti, jei atspėjote neteisingai? Patikrinkim! Mes jį kvadratu, naudodami sumos kvadrato formulę:
Teisingai.) Bet... Iš kur aš gavau tokį posakį? Iš dangaus?
Ne.) Sąžiningai jį sumažinsime. Paprasčiausiai naudodamas šią išraišką aš tiksliai parodysiu, kaip užduočių autoriai užšifruoja tokius kvadratus. :) Kas yra 54? Tai pirmojo ir antrojo skaičių kvadratų suma. Ir, atkreipkite dėmesį, jau be šaknų! Ir šaknis lieka viduje dvigubas produktas, kuris mūsų atveju yra lygus . Todėl tokių pavyzdžių aiškinimas prasideda nuo dvigubo produkto paieškos. Jei išnarpliojate su įprasta atranka. Ir, beje, apie ženklus. Čia viskas paprasta. Jei prieš dvigubą yra pliusas, tada sumos kvadratas. Jei tai minusas, tai skirtumai.) Turime pliusą – tai reiškia sumos kvadratą.) O dabar – žadėtasis analitinis dekodavimo metodas. Per sistemą.)
Taigi po mūsų šaknimi aiškiai slypi posakis (a+b) 2, o mūsų užduotis yra surasti a Ir b. Mūsų atveju kvadratų suma duoda 54. Taigi rašome:
![]()
Dabar padvigubinkite produktą. Mes jį turime. Taigi užrašome:
Turime tokią sistemą:
![]()
Išsprendžiame įprastu pakeitimo metodu. Pavyzdžiui, išreiškiame iš antrosios lygties ir pakeičiame ją pirmąja:

Išspręskime pirmąją lygtį:
Gauta bikvadratinis lygtis santykinėa . Apskaičiuojame diskriminantą:
Reiškia,
Gavome net keturias galimas reikšmesa. Mes nebijome. Dabar išrausime visus nereikalingus dalykus.) Jei dabar apskaičiuosime atitinkamas kiekvienos iš keturių rastų verčių reikšmes, gausime keturis mūsų sistemos sprendimus. Štai jie:
Ir čia kyla klausimas – kuris sprendimas mums tinka? Pagalvokime apie tai. Neigiamus sprendimus galima iš karto atmesti: kvadratuojant „išdegs“ minusai, o visa radikali išraiška kaip visuma nepasikeis.) Lieka pirmieji du variantai. Galite juos pasirinkti visiškai savavališkai: perstačius terminus suma vis tiek nesikeičia.) Tegul, pavyzdžiui, , a .
Iš viso gavome šios sumos kvadratą po šaknimi:
Viskas aišku.)
Ne veltui taip išsamiai aprašinėju sprendimo procesą. Kad būtų aišku, kaip vyksta iššifravimas.) Tačiau yra viena problema. Analitinis dekodavimo metodas, nors ir patikimas, yra labai ilgas ir gremėzdiškas: reikia išspręsti bikvadratinę lygtį, gauti keturis sistemos sprendinius ir tada dar galvoti, kuriuos pasirinkti... Vargina? Sutinku, tai vargina. Šis metodas veikia nepriekaištingai daugumoje šių pavyzdžių. Tačiau labai dažnai galite sutaupyti daug darbo ir kūrybiškai rasti abu skaičius. Pagal pasirinkimą.) Taip, taip! Dabar, naudodamas antrojo termino (antrosios šaknies) pavyzdį, parodysiu lengvesnį ir greitesnį išskyrimo būdą pilna aikštė po šaknimi.
Taigi dabar turime šią šaknį: ![]() .
.
Pagalvokime taip: „Po šaknimi greičiausiai yra užšifruotas pilnas kvadratas. Kai prieš dublį yra minusas, tai reiškia skirtumo kvadratą. Pirmojo ir antrojo skaičių kvadratų suma suteikia mums skaičių 54. Bet kokie tai kvadratai? 1 ir 53? 49 ir 5 ? Per daug variantų... Ne, geriau pradėti išpainioti nuo dvigubo produkto. Mūsųgali būti parašytas kaip. Times produktas padvigubėjo, tada iškart atmetame abu. Tada kandidatai į vaidmenį a ir b lieka 7 ir . O jei 14 ir/2 ? Tai įmanoma. Bet mes visada pradedame nuo kažko paprasto! Taigi, tegul . Patikrinkime jų kvadratų sumą:
Suveikė! Tai reiškia, kad mūsų radikali išraiška iš tikrųjų yra skirtumo kvadratas:
Čia yra lengvas būdas išvengti problemų su sistema. Tai ne visada veikia, bet daugelyje šių pavyzdžių to visiškai pakanka. Taigi, po šaknimis yra pilni kvadratai. Belieka teisingai ištraukti šaknis ir apskaičiuoti pavyzdį:
Dabar pažvelkime į dar nestandartinę užduotį dėl šaknų.)
Įrodykite, kad skaičius A– sveikasis skaičius, jei .
Tiesiogiai nieko neišgaunama, šaknys įleistos, ir net įvairaus laipsnio... Košmaras! Tačiau užduotis turi prasmę.) Todėl yra jos sprendimo raktas.) O čia svarbiausia yra tai. Apsvarstykite mūsų lygybę
Kaip lygtis santykinė A. Taip, taip! Būtų malonu atsikratyti šaknų. Mūsų šaknys yra kubinės, todėl supjaustykime abi lygties puses. Pagal formulę sumos kubas:

Kubai ir kubinės šaknys panaikina vienas kitą, o po kiekviena didele šaknimi paimame po vieną skliaustelį iš kvadrato ir skirtumo bei sumos sandaugą sutraukiame į kvadratų skirtumą:
Atskirai apskaičiuojame kvadratų skirtumą po šaknimis:
Identiškos išraiškų transformacijos yra viena iš mokyklinio matematikos kurso turinio eilučių. Identiškos transformacijos plačiai naudojamos sprendžiant lygtis, nelygybes, lygčių ir nelygybių sistemas. Be to, identiškos išraiškų transformacijos prisideda prie intelekto, mąstymo lankstumo ir racionalumo ugdymo.
Siūloma medžiaga skirta 8 klasės mokiniams ir apima teorinius pagrindus tapatybės transformacijos racionalus ir ir racionalios išraiškos, tokių posakių transformavimo užduočių tipai ir testo tekstas.
1. Tapatybės transformacijų teoriniai pagrindai
Algebros išraiškos yra įrašai, susidedantys iš skaičių ir raidžių, sujungtų veiksmo ženklais.
https://pandia.ru/text/80/197/images/image002_92.gif" width="77" height="21 src=">.gif" width="20" height="21 src="> – algebrinės išraiškos.
Priklausomai nuo operacijų, skiriamos racionalios ir neracionalios išraiškos.
Algebrinės išraiškos vadinamos racionaliosiomis, jei jos yra susijusios su joje esančiomis raidėmis A, b, Su, ... nevykdomos jokios kitos operacijos, išskyrus sudėtį, daugybą, atimtį, dalybą ir eksponenciją.
Algebrinės išraiškos, kuriose yra kintamojo šaknies ištraukimo arba kintamojo padidinimo į racionalus laipsnis, kurie nėra sveikasis skaičius, yra vadinami neracionaliais šio kintamojo atžvilgiu.
Per identišką transformaciją duota išraiška vadinamas vienos išraiškos pakeitimu kita, identiškai lygia jai tam tikroje aibėje.
Šie teoriniai faktai yra identiškų racionalių ir neracionalių išraiškų transformacijų pagrindas.
1. Laipsnių su sveikuoju rodikliu savybės:
![]() , nĮJUNGTA; A 1=A;
, nĮJUNGTA; A 1=A;
, nĮJUNGTA, A¹0; A 0=1, A¹0;
![]() , A¹0;
, A¹0;
, A¹0;
, A¹0;
, A¹0, b¹0;
![]() , A¹0, b¹0.
, A¹0, b¹0.
2. Sutrumpintos daugybos formulės:
Kur A, b, Su– bet kokie realieji skaičiai;
Kur A¹0, X 1 ir X 2 – lygties šaknys ![]() .
.
3. Pagrindinė trupmenų savybė ir veiksmai su trupmenomis:
![]() , Kur b¹0, Su¹0;
, Kur b¹0, Su¹0;
; ![]() ;
;
4. Aritmetinės šaknies apibrėžimas ir jos savybės:
![]() ; , b#0; https://pandia.ru/text/80/197/images/image026_24.gif" width="84" height="32">; ;
; , b#0; https://pandia.ru/text/80/197/images/image026_24.gif" width="84" height="32">; ; ![]() ,
,
Kur A, b – neneigiami skaičiai, nĮJUNGTA, n³2, mĮJUNGTA, m³2.
1. Išraiškos konvertavimo pratimai
Yra įvairių tipų pratimai identiškoms išraiškų transformacijoms. Pirmasis tipas: Konversija, kurią reikia atlikti, yra aiškiai nurodyta.
Pavyzdžiui.
1. Pavaizduokite jį kaip daugianarį.
Atlikdami šią transformaciją, naudojome daugianario daugybos ir atimties taisykles, sutrumpinto daugybos formulę ir panašių narių redukciją.
2. Atsižvelgti į: ![]() .
.
Atlikdami transformaciją naudojome pašalinimo taisyklę bendras daugiklis už skliaustas ir 2 sutrumpintos daugybos formulės.
3. Sumažinkite trupmeną:
![]() .
.

Atlikdami transformaciją naudojome bendrojo koeficiento pašalinimą iš skliaustų, komutacinius ir susitraukimo dėsnius, 2 sutrumpintas daugybos formules ir operacijas laipsniais.
4. Pašalinkite faktorių iš po šaknies ženklo if A³0, b³0, Su³0: https://pandia.ru/text/80/197/images/image036_17.gif" width="432" height="27">
Naudojome taisykles veiksmams su šaknimis ir skaičiaus modulio apibrėžimą.
5. Pašalinkite trupmenos vardiklio neracionalumą. ![]() .
.
Antrasis tipas pratimai – tai pratimai, kuriuose aiškiai nurodoma pagrindinė transformacija, kurią reikia atlikti. Tokiose pratybose reikalavimas paprastai formuluojamas viena iš šių formų: supaprastinti išraišką, apskaičiuoti. Atliekant tokius pratimus, visų pirma reikia nustatyti, kokias ir kokia tvarka reikia atlikti transformacijas, kad išraiška įgautų kompaktiškesnę formą nei duotoji, arba gautas skaitinis rezultatas.
Pavyzdžiui
6. Supaprastinkite posakį:
Sprendimas:
![]() .
.
Naudotos algebrinių trupmenų ir sutrumpintų daugybos formulių veikimo taisyklės.
7. Supaprastinkite posakį:
 .
.
Jeigu A³0, b³0, A¹ b.
Naudojome sutrumpintas daugybos formules, trupmenų pridėjimo ir neracionalių išraiškų dauginimo taisykles, tapatybę https://pandia.ru/text/80/197/images/image049_15.gif" width="203" height="29">.
Naudojome viso kvadrato, tapatybės https://pandia.ru/text/80/197/images/image053_11.gif" width="132 height=21" height="21"> pasirinkimo operaciją, jei .
Įrodymas:
Nuo tada ir arba arba arba arba , t.y.
Naudojome kubų sumos sąlygą ir formulę.
Reikėtų nepamiršti, kad sąlygos, jungiančios kintamuosius, taip pat gali būti nurodytos pirmųjų dviejų tipų pratybose.
Pavyzdžiui.
10. Raskite, jei .
Mums svarbu išlaikyti jūsų privatumą. Dėl šios priežasties sukūrėme Privatumo politiką, kurioje aprašoma, kaip naudojame ir saugome jūsų informaciją. Peržiūrėkite mūsų privatumo praktiką ir praneškite mums, jei turite klausimų.
Asmeninės informacijos rinkimas ir naudojimas
Asmeninė informacija reiškia duomenis, kurie gali būti naudojami konkretaus asmens tapatybei nustatyti arba susisiekti su juo.
Jūsų gali būti paprašyta pateikti savo asmeninę informaciją bet kuriuo metu, kai susisiekiate su mumis.
Toliau pateikiami keli pavyzdžiai, kokios rūšies asmeninės informacijos galime rinkti ir kaip galime tokią informaciją naudoti.
Kokią asmeninę informaciją renkame:
- Kai svetainėje pateikiate užklausą, galime surinkti įvairios informacijos, įskaitant jūsų vardą, telefono numerį, adresą paštu ir tt
Kaip naudojame jūsų asmeninę informaciją:
- Mūsų surinkta asmeninė informacija leidžia susisiekti su jumis ir informuoti apie unikalius pasiūlymus, akcijas ir kitus renginius bei artėjančius renginius.
- Retkarčiais galime naudoti jūsų asmeninę informaciją svarbiems pranešimams ir pranešimams siųsti.
- Mes taip pat galime naudoti asmeninę informaciją vidiniais tikslais, tokiais kaip auditas, duomenų analizė ir įvairūs tyrimai siekdami pagerinti mūsų teikiamas paslaugas ir teikti rekomendacijas dėl mūsų paslaugų.
- Jei dalyvaujate prizų traukime, konkurse ar panašioje akcijoje, mes galime naudoti jūsų pateiktą informaciją tokioms programoms administruoti.
Informacijos atskleidimas trečiosioms šalims
Mes neatskleidžiame iš jūsų gautos informacijos trečiosioms šalims.
Išimtys:
- Esant poreikiui – įstatymų nustatyta tvarka, teismine tvarka, teismine tvarka ir (arba) remiantis viešais prašymais ar prašymais iš vyriausybines agentūras Rusijos Federacijos teritorijoje – atskleiskite savo asmeninę informaciją. Taip pat galime atskleisti informaciją apie jus, jei nuspręsime, kad toks atskleidimas yra būtinas arba tinkamas saugumo, teisėsaugos ar kitais visuomenei svarbiais tikslais.
- Reorganizavimo, susijungimo ar pardavimo atveju surinktą asmeninę informaciją galime perduoti atitinkamai trečiajai šaliai.
Asmeninės informacijos apsauga
Mes imamės atsargumo priemonių, įskaitant administracines, technines ir fizines, siekdami apsaugoti jūsų asmeninę informaciją nuo praradimo, vagystės ir netinkamo naudojimo, taip pat nuo neteisėtos prieigos, atskleidimo, pakeitimo ir sunaikinimo.
Jūsų privatumo gerbimas įmonės lygiu
Siekdami užtikrinti, kad jūsų asmeninė informacija būtų saugi, savo darbuotojams pranešame apie privatumo ir saugumo standartus ir griežtai vykdome privatumo praktiką.
Straipsnyje atskleidžiama neracionalių posakių reikšmė ir transformacijos jomis. Panagrinėkime pačią neracionalių posakių sampratą, transformaciją ir būdingas išraiškas.
Yandex.RTB R-A-339285-1
Kas yra neracionalios išraiškos?
Įvesdami šaknis mokykloje, tiriame iracionalių posakių sampratą. Tokie posakiai yra glaudžiai susiję su šaknimis.
1 apibrėžimas
Neracionalios išraiškos yra išraiškos, turinčios šaknį. Tai yra, tai yra posakiai, turintys radikalų.
Remiantis šis apibrėžimas, turime, kad x - 1, 8 3 3 6 - 1 2 3, 7 - 4 3 (2 + 3) , 4 a 2 d 5: d 9 2 a 3 5 yra neracionalaus tipo išraiškos.
Nagrinėdami išraišką x · x - 7 · x + 7 x + 3 2 · x - 8 3 matome, kad išraiška yra racionali. Racionaliosios išraiškos apima daugianario ir algebrinės trupmenos. Neracionalūs apima darbą su logaritmines išraiškas arba radikalios išraiškos.
Pagrindiniai neracionalių posakių transformacijų tipai
Skaičiuojant tokias išraiškas, būtina atkreipti dėmesį į DZ. Jie dažnai reikalauja papildomos transformacijos atidaromų skliaustų pavidalu, liejimas panašių narių, grupės ir pan. Tokių transformacijų pagrindas yra operacijos su skaičiais. Iracionalių posakių transformacijos laikosi griežtos tvarkos.
1 pavyzdys
Pakeiskite išraišką 9 + 3 3 - 2 + 4 · 3 3 + 1 - 2 · 3 3 .
Sprendimas
Būtina pakeisti skaičių 9 išraiška, kurioje yra šaknis. Tada mes tai gauname
81 + 3 3 - 2 + 4 3 3 + 1 - 2 3 3 = = 9 + 3 3 - 2 + 4 3 3 + 1 - 2 3 3
Gauta išraiška turi panašius terminus, todėl atlikime liejimą ir grupavimą. Mes gauname
9 + 3 3 - 2 + 4 3 3 + 1 - 2 3 3 = = 9 - 2 + 1 + 3 3 + 4 3 3 - 2 3 3 = = 8 + 3 3 3
Atsakymas: 9 + 3 3 - 2 + 4 3 3 + 1 - 2 3 3 = 8 + 3 3 3
2 pavyzdys
Pateikite išraišką x + 3 5 2 - 2 · x + 3 5 + 1 - 9 kaip dviejų iracionaliųjų sandaugą, naudodami sutrumpintas daugybos formules.
Sprendimai
x + 3 5 2 - 2 x + 3 5 + 1 - 9 = = x + 3 5 - 1 2 - 9
9 pavaizduojame 3 2 pavidalu ir taikome kvadratų skirtumo formulę:
x + 3 5 - 1 2 - 9 = x + 3 5 - 1 2 - 3 2 = = x + 3 5 - 1 - 3 x + 3 5 - 1 + 3 = = x + 3 5 - 4 x + 3 5 + 2
Identiškų transformacijų rezultatas lėmė dviejų racionalių išraiškų, kurias reikėjo rasti, sandaugą.
Atsakymas:
x + 3 5 2 - 2 x + 3 5 + 1 - 9 = = x + 3 5 - 4 x + 3 5 + 2
Galite atlikti daugybę kitų transformacijų, taikomų neracionalioms išraiškoms.
Radikalios išraiškos konvertavimas
Svarbu tai, kad po šaknies ženklu esanti išraiška gali būti pakeista identiškai jam lygiaverte. Šis teiginys leidžia dirbti su radikalia išraiška. Pavyzdžiui, 1 + 6 galima pakeisti 7 arba 2 · a 5 4 - 6 2 · a 4 · a 4 - 6 . Jie yra identiški, todėl pakeitimas prasmingas.
Kai nėra 1, besiskiriančio nuo a, kur galioja a n = a 1 n formos nelygybė, tada tokia lygybė galima tik esant a = a 1. Tokių išraiškų reikšmės yra lygios bet kurioms kintamųjų reikšmėms.
Šakninių savybių naudojimas
Šaknų savybės naudojamos išraiškoms supaprastinti. Taikant savybę a · b = a · b, kur a ≥ 0, b ≥ 0, tada iš iracionalios formos 1 + 3 · 12 gali tapti identiškai lygi 1 + 3 · 12. Turtas. . . a n k n 2 n 1 = a n 1 · n 2 · , . . . , · n k , kur a ≥ 0 reiškia, kad x 2 + 4 4 3 gali būti parašytas x 2 + 4 24 forma.
Konvertuojant radikalias išraiškas yra keletas niuansų. Jei yra išraiška, tai - 7 - 81 4 = - 7 4 - 81 4 negalime jos užrašyti, nes formulė a b n = a n b n tarnauja tik neneigiamam a ir teigiamam b. Jei savybė pritaikyta teisingai, rezultatas bus 7 4 81 4 formos išraiška.
Teisingai transformacijai naudojamos neracionalių išraiškų transformacijos naudojant šaknų savybes.
Daugiklio įvedimas po šaknies ženklu
3 apibrėžimasPadėkite po šaknies ženklu– reiškia pakeisti išraišką B · C n, o B ir C yra kai kurie skaičiai arba išraiškos, kur n yra natūralusis skaičius, didesnis nei 1, lygiavertė išraiška, kurios forma yra B n · C n arba - B n · C n .
Jei formos išraišką supaprastinsime 2 x 3, tai pridėję ją prie šaknies gausime, kad 2 3 x 3. Tokios transformacijos galimos tik po to išsamus tyrimas daugiklio įvedimo po šaknies ženklu taisyklės.
Daugiklio pašalinimas iš po šaknies ženklo
Jei yra B n · C n formos išraiška, tada ji redukuojama į formą B · C n , kur yra nelyginių n , kurie turi formą B · C n , kai lyginiai n , B ir C yra kai kurie skaičiai ir posakius.
Tai yra, jei imsime neracionalią 2 3 x 3 formos išraišką, pašalinsime faktorių iš po šaknies, tada gausime išraišką 2 x 3. Arba x + 1 2 · 7 bus x + 1 · 7 formos išraiška, kuri turi kitą formos x + 1 · 7 žymėjimą.
Norint supaprastinti išraišką ir ją, būtina pašalinti veiksnį iš po šaknies greitas konvertavimas.
Konvertuojamos trupmenos, kuriose yra šaknų
Neracionali išraiška gali būti kaip natūralusis skaičius, ir trupmenos pavidalu. Norėdami konvertuoti trupmeninės išraiškos didelis dėmesys sumokėti iki jo vardiklio. Jei paimsime formos trupmeną (2 + 3) x 4 x 2 + 5 3, tada skaitiklis įgaus formą 5 x 4 ir, pasinaudoję šaknų savybėmis, pamatysime, kad vardiklis bus x 2 + 5 6. Pradinė trupmena gali būti parašyta kaip 5 x 4 x 2 + 5 6.
Būtina atkreipti dėmesį į tai, kad reikia keisti tik skaitiklio arba tik vardiklio ženklą. Mes tai gauname
X + 2 x - 3 x 2 + 7 4 = x + 2 x - (- 3 x 2 + 7 4) = x + 2 x 3 x 2 - 7 4
Supaprastinant dažniausiai naudojamas trupmenos sumažinimas. Mes tai gauname
3 · x + 4 3 - 1 · x x + 4 3 - 1 3 sumažinti x + 4 3 - 1 . Gauname išraišką 3 x x + 4 3 - 1 2.
Prieš redukciją būtina atlikti transformacijas, kurios supaprastina išraišką ir suteikia galimybę faktorizuoti sudėtinga išraiška. Dažniausiai naudojamos sutrumpintos daugybos formulės.
Jei imsime formos 2 · x - y x + y trupmeną, tada reikia įvesti naujus kintamuosius u = x ir v = x, tada duota išraiška pakeis formą ir taps 2 · u 2 - v 2 u + v. Skaitiklis turėtų būti išskaidytas į daugianario formulę, tada mes tai gauname
2 · u 2 - v 2 u + v = 2 · (u - v) · u + v u + v = 2 · u - v. Atlikę atvirkštinį pakeitimą, gauname formą 2 x - y, kuri yra lygi pradinei.
Leidžiama sumažinti iki naujo vardiklio, tada reikia skaitiklį padauginti iš papildomo koeficiento. Jei imsime formos x 3 trupmeną - 1 0, 5 · x, tai ją sumažiname iki vardiklio x. Norėdami tai padaryti, skaitiklį ir vardiklį reikia padauginti iš išraiškos 2 x, tada gauname išraišką x 3 - 1 0, 5 x = 2 x x x 3 - 1 0, 5 x 2 x = 2 x x 3 - 1 x .
Sumažinti frakcijas arba atvesti panašias reikia tik nurodytos frakcijos ODZ. Kai skaitiklį ir vardiklį padauginame iš neracionalios išraiškos, pastebime, kad vardiklyje atsikratome neracionalumo.
Iracionalumo atsikratymas vardiklyje
Kai išraiška transformacijos būdu atsikrato vardiklio šaknies, tai vadinama neracionalumo atsikratymu. Pažiūrėkime į formos x 3 3 trupmenos pavyzdį. Atsikratę iracionalumo, gauname naują 9 3 x 3 formos trupmeną.
Perėjimas nuo šaknų prie galių
Perėjimai nuo šaknų prie galių yra būtini norint greitai transformuoti neracionalias išraiškas. Jei laikysime lygybę a m n = a m n , pamatysime, kad ją naudoti galima, kai a yra teigiamas skaičius, m yra sveikas skaičius, o n yra natūralusis skaičius. Jei laikysime išraišką 5 - 2 3, tai kitu atveju turime teisę rašyti kaip 5 - 2 3. Šios išraiškos yra lygiavertės.
Kai šaknyje yra neigiamas skaičius arba skaičius su kintamaisiais, tada formulė a m n = a m n ne visada taikoma. Jei tokias šaknis (- 8) 3 5 ir (- 16) 2 4 reikia pakeisti laipsniais, tai gauname, kad - 8 3 5 ir - 16 2 4 pagal formulę a m n = a m n su neigiamuoju a nedirbame. Norint išsamiai išanalizuoti radikalių posakių ir jų supaprastinimų temą, būtina išstudijuoti straipsnį apie perėjimą nuo šaknų prie galių ir atgal. Reikia atsiminti, kad formulė a m n = a m n netaikoma visoms šio tipo išraiškoms. Iracionalumo atsikratymas prisideda prie tolesnio išraiškos supaprastinimo, jos transformacijos ir sprendimo.
Jei tekste pastebėjote klaidą, pažymėkite ją ir paspauskite Ctrl+Enter








