Atskirti specialūs taškai internete. Laurent serijos išskirti vienaskaitos taškai ir jų klasifikacija

Taylor gretos tarnauja veiksmingomis priemonėmis analitinėms funkcijoms tirti apskritime zol Analitinėms funkcijoms tirti žiedo srityje pasirodo, kad galima sukonstruoti Taylor plėtinius apibendrinančios formos teigiamų ir neigiamų galių (z - zq) plėtinius. Serija (1), suprantama kaip dviejų serijų suma, vadinama Laurent serija. Akivaizdu, kad (1) eilutės konvergencijos sritis yra bendroji dalis kiekvienos eilutės konvergencijos sritis (2). Suraskime ją. Pirmosios serijos konvergencijos sritis yra apskritimas, kurio spindulys nustatomas pagal Cauchy-Hadamard formulę. absoliučiai ir vienodai. Antroji eilutė yra galios serija kintamojo atžvilgiu serija (5) susilieja savo konvergencijos apskritimo viduje į kompleksinio kintamojo m-*oo analitinę funkciją ir bet kuriame mažesnio spindulio apskritime konverguoja absoliučiai ir tolygiai, o tai reiškia, kad konvergencijos sritis serijos (4) yra apskritimo išorė – jei tada egzistuoja bendroji sritis(3) ir (4) eilučių konvergencija – apskritas žiedas, kuriame serija (1) susilieja į analitinę funkciją. Be to, bet kuriame žiede jis susilieja absoliučiai ir vienodai. 1 pavyzdys. Nustatykite rad Laurent serijos konvergencijos plotą Atskirti vienaskaitos taškai ir jų klasifikacija M Pirmos eilutės konvergencijos sritis yra apskritimo išorė, o antrosios eilutės konvergencijos sritis yra apskritimo viduje Taigi, ši serija konverguoja kola"o 15 teorema. Bet kuri funkcija f(z), vienareikšmė ir apolitiška apskritimo žiede, gali būti pavaizduota šiame žiede kaip konvergentinės eilutės suma, kurios koeficientai Cn yra vienareikšmiai nustatomi ir apskaičiuojami formulės, kur 7p yra apskritimas, kurio spindulys yra m. Sukonstruokime apskritimus su centrais taške r, kurių spinduliai tenkina nelygybes ir panagrinėkime naująjį Po žiedą integralinė teorema Cauchy daugybiškai sujungtam domenui Transformuokime atskirai kiekvieną sumos (8) integralą. Visiems taškams £ išilgai apskritimo 7d* yra patenkintas tolygiai konvergencinės eilutės 1 1 sumos santykis. integruojant išilgai apskritimo, gauname, kad antrojo integralo transformaciją atliekame kiek kitaip Visiems taškams £ apskritime ir> kaip tolygiai susiliejančių eilučių sumą, padauginus abi dalis iš ištisinės funkcijos) ir integruojant išilgai apskritimo 7/, gauname, kad Atkreipkite dėmesį, kad (10) ir (12) formulės yra analitinės funkcijos apskritimo žiede. Todėl pagal Cauchy teoremą atitinkamų integralų reikšmės nepasikeis, jei apskritimus 7/r ir 7r/ pakeisime bet kuriuo apskritimu. Tai leidžia sujungti formules (10) ir (12) , pakeičiant integralus dešinėje (8) formulės pusėje su jų išraiškomis (9) ir (11) atitinkamai gauname norimą išplėtimą Kadangi z - savavališkas taškasžiedas, tada seka (14) konverguoja į funkciją f(z) visame šiame žiede, o bet kuriame žiede serija absoliučiai ir tolygiai suartėja su šia funkcija. Dabar įrodykime, kad formos (6) skaidymas yra unikalus. Tarkime, kad yra dar vienas išplėtimas. Tada visur žiedo R viduje turėsime Apskritime serijos (15) susilieja tolygiai. Padauginkime abi lygybės puses (kur m yra fiksuotas sveikasis skaičius, ir integruokime abi eilutes po termino. Dėl to kairėje pusėje gauname, o dešinėje - Sch. Taigi, (4, = St. Kadangi m - savavališkas skaičius, tada paskutinė lygybė įrodo skilimo unikalumą. Serija (6), kurios koeficientai apskaičiuojami naudojant (7) formules, vadinama funkcijos f(z) Laurent'o eilute neigiamų galių vadinama teisinga Laurent serijos dalimi, o su neigiamomis – jos pagrindinė dalis. Laurent serijos koeficientų formulės (7) praktiškai naudojamos retai, nes paprastai joms reikia sudėtingų skaičiavimų. Paprastai, jei įmanoma, naudojami paruošti Taylor išplėtimai elementarios funkcijos. Remiantis dekompozicijos unikalumu, bet koks teisinis metodas leidžia pasiekti tą patį rezultatą. 2 pavyzdys. Apsvarstykite funkcijos Laurent serijos išplėtimus įvairiose srityse, priimant Fuiscia /(g) yra du vienaskaitos taškai: . Vadinasi, yra trys žiedinės sritys, kurių centras yra taške r = 0. Kiekvienoje iš jų funkcija f(r) yra analitinė: a) apskritimas yra žiedas, apskritimo išorė (27 pav.). Raskime funkcijos /(z) Laurent plėtinius kiekviename iš šių regionų. Pavaizduokime /(z) kaip elementariųjų trupmenų sumą a) Apskritimas Santykį (16) transformuojame taip geometrinė progresija, gauname Pakeiskite rastus plėtinius į formulę (17): Šis išplėtimas yra funkcijos /(z) Teiloro eilutė. b) Funkcijos -r žiedas šiame žiede išlieka konvergentinis, nes funkcijos j^j serija (19) yra |z| > 1 skiriasi. Todėl funkciją /(z) transformuojame taip: dar kartą taikydami formulę (19), gauname, kad Ši serija konverguoja. Pakeitę plėtinius (18) ir (21) į santykį (20), gauname c) funkcijos -z apskritimo išorę |z| > 2 skiriasi, o eilė (21) funkcijai – funkciją /(z) pavaizduok tokia forma: /<*>Naudodami (18) ir (19) formules gauname ARBA 1 Šis pavyzdys rodo, kad tai pačiai funkcijai f(z) Laurent išplėtimas paprastai turi skirtingos rūšies skirtingiems žiedams. 3 pavyzdys. Raskite funkcijos Laurent serijos 8-osios Laurent serijos išplėtimą. Išskirti vienaskaitos taškai ir jų klasifikacija žiedo srityje A Mes naudojame funkcijos f(z) atvaizdavimą tokia forma: ir transformuojame antrąjį terminą Naudojant geometrinės progresijos narių sumos formulę, gauname Pakeitę rastas išraiškas į formulę (22), turime 4 pavyzdį. Išplėskite funkciją Laurent'o eilutėje taške zq = 0. Bet kuriam kompleksui mes įdedame tai išplėtimas galioja bet kuriam taškui z Ф 0. In šiuo atvejužiedinė sritis vaizduoja visą kompleksinę plokštumą su vienu išmestu tašku z - 0. Ši sritis gali būti apibrėžta tokiu ryšiu: Ši funkcija yra analitinė srityje Iš formulių (13) Laurent'o serijos koeficientams, naudojant tą patį samprotaujant, kaip ir ankstesnėje pastraipoje, galima gauti nelygybes Kouiw. jei funkcija f(z) yra apribota apskritimu, kur M yra konstanta), tai Izoliuoti vienaskaitos taškai Taškas zo vadinamas funkcijos f(z) izoliuotu vienaskaitos tašku, jei taško (() yra žiedinė kaimynystė ši aibė kartais vadinama taško 2o punkcija kaimynyste, kurioje funkcija f(z) yra unikali ir analitinė. Pačiame taške zo funkcija yra arba neapibrėžta, arba nedviprasmiška ir analitinė. Priklausomai nuo funkcijos /(r) elgesio artėjant prie taško zo, išskiriami trys tipai: vienetiniai taškai. Sakoma, kad izoliuotas vienaskaitos taškas yra: 1) pašalinamas, jei yra baigtinis 2) pmusach, jei 3) iš esmės vienaskaita, jei funkcija f(z) neturi ribos ties Izoliuoto vienaskaitos taško tipas yra glaudžiai susijęs su funkcijos Laurento išplėtimo pobūdis pradurtu centru. 16 teorema. Funkcijos f(z) izoliuotas vienaskaitos taškas z0 yra pašalinamas vienaskaitos taškas tada ir tik tada, kai funkcijos f(z) Laurent'o plėtinyje taško zo kaimynystėje nėra pagrindinės dalies, t.y. turi formą Tegul zo yra nuimamas vienaskaitos taškas. Tada yra baigtinė, todėl funkcija f(z) yra ribojama prokologinėje taško z kaimynystėje. Mes įdedame Dėl Koši nelygybių Kadangi p gali būti pasirinktas savavališkai mažas, tai visi koeficientai esant neigiamiems laipsniams (z). - 20) yra lygūs nuliui: Ir atvirkščiai, tegul Laurent'o funkcijos /(r) išplėtimas taško zq kaimynystėje turi tik teisingą dalį, tai yra, jos forma (23) ir todėl yra Teiloras. Nesunku pastebėti, kad z -* z0 funkcija /(z) turi ribinę reikšmę: 17 teorema. Funkcijos f(z) izoliuotas vienaskaitos taškas zq yra pašalinamas tada ir tik tada, kai funkcija J(z) yra ribojasi tam tikroje pradurtoje taško zq kaimynystėje, Zgmechai ne. Tegul r yra nuimamas funkcijos /(r) vienaskaitos taškas. Darant prielaidą, kad funkcija /(r) yra analitinė tam tikrame apskritime, kurio centras yra taške r. Taip nustatomas taško pavadinimas – nuimamas. 18 teorema. Funkcijos f(z) izoliuotas vienaskaitos taškas zq yra polius tada ir tik tada Funkcijos f(z) Laurent išplėtimas taško kaimynystėje turi baigtinį (ir teigiamą) skaičių nenulinių dėmenų, t.y. jis turi formą 4 Tegul z0 yra polius. Nuo tada taško z0 yra pradurta kaimynystė, kurioje funkcija f(z) yra analitinė ir nulinė. Tada šioje kaimynystėje yra apibrėžta analitinė funkcija ir todėl taškas zq yra nuimamas funkcijos vienaskaitos taškas (nulis) arba kur h(z) yra analitinė funkcija, h(z0) Φ 0. Tada h(zo) Φ 0 taip pat yra analitinė, tada funkcija u yra analitinė taško zq kaimynystėje, todėl iš kur gauname, kad dabar tarkime, kad funkcija f(z) turi formos (24) išplėtimą taško zо punkcinėje kaimynystėje. Tai reiškia, kad šioje kaimynystėje funkcija f(z) yra analitinė kartu su funkcija. Funkcijai g(z) galioja plėtinys, iš kurio matyti, kad zq yra nuimamas funkcijos g(z) taškas, tada funkcija, esanti 0, yra funkcijos polius yra dar vienas paprastas faktas. Taškas Zq yra funkcijos f(z) polius tada ir tik tada, jei funkcija g(z) = yj gali būti išplėsta iki analitinės funkcijos, esančios taško zq kaimynystėje, nustatant g(z0) = 0. funkcijos f(z) poliaus vadinamas funkcijos jfa nuline eile. Iš 16 ir 18 teoremų išplaukia kitas pareiškimas. 19 teorema. Izoliuotas vienaskaitos taškas iš esmės yra vienaskaita tada ir tik tada, kai pagrindinėje Laurento plėtimo dalyje šio taško pradūrtoje kaimynystėje yra be galo daug nulinių dalių. 5 pavyzdys. Funkcijos vienaskaitos taškas yra zo = 0. Turime Laurent seriją Išskirti vienaskaitos taškai ir jų klasifikacija Todėl zo = O yra pašalinamas vienaskaitos taškas. Funkcijos /(z) išplėtimas į Laurent seriją kaimynystėje nulinis taškas yra tik teisinga dalis: 7 pavyzdys. /(z) = Funkcijos f(z) vienaskaitos taškas yra zq = 0. Panagrinėkime šios funkcijos elgseną tikrosioje ir įsivaizduojamoje ašyse: on tikroji ašis ties x 0, įsivaizduojamoje ašyje Todėl nei baigtinis, nei begalinė riba f(z) neegzistuoja z -* 0. Tai reiškia, kad taškas r = 0 iš esmės yra funkcijos f(z) vienaskaita. Raskime funkcijos f(z) Laurent'o plėtinį nulinio taško apylinkėse. Bet kuriam kompleksui C turime rinkinį. Tada Laurent plėtinyje yra demonas galutinis skaičius terminai su neigiamomis z galiomis.

Dviejų autonominių sistemų aprašyti modeliai diferencialines lygtis.

Fazinė plokštuma. Fazinis portretas. Isoclin metodas. Pagrindinės izoklinos. Tvarumas pastovi būsena. Linijinės sistemos. Vienaskaitos taškų tipai: mazgas, balnas, židinys, centras. Pavyzdys: cheminės reakcijos pirmas užsakymas.

Įdomiausi rezultatai apie kokybinį biologinių sistemų savybių modeliavimą buvo gauti naudojant dviejų diferencialinių lygčių modelius, kurie leidžia kokybinis tyrimas naudojant metodą fazinė plokštuma. Apsvarstykite dviejų autonominių įprastų diferencialinių lygčių sistemą bendras vaizdas

(4.1)

P(x,y), Q(x,y)- nuolatinės funkcijos, apibrėžta tam tikroje srityje G Euklido plokštuma ( x,y ‑ Dekarto koordinatės) ir šioje srityje turinčios ne žemesnės nei pirmosios eilės išvestines.

Regionas G gali būti neribotas arba ribotas. Jei kintamieji x, y turi specifinę biologinę reikšmę (medžiagų koncentracijos, rūšių skaičius) dažniausiai plotas G reiškia teigiamą dešinės pusės plokštumos kvadrantą:

0 £ x< ¥ ,0 £ y< ¥ .

Medžiagų koncentraciją arba rūšių skaičių iš viršaus taip pat gali apriboti laivo tūris arba buveinės plotas. Tada kintamųjų diapazonas turi tokią formą:

0 £ x< x 0 , 0 £ y< y 0 .

Kintamieji x, y laiko pokytis pagal lygčių sistemą (4.1), kad kiekviena sistemos būsena atitiktų kintamųjų reikšmių porą ( x, y).

Ir atvirkščiai, kiekviena kintamųjų pora ( x, y) atitinka tam tikrą sistemos būseną.

Apsvarstykite plokštumą su koordinačių ašimis, kuriose brėžiamos kintamųjų reikšmės x,y. Kiekvienas taškas Mši plokštuma atitinka tam tikrą sistemos būseną. Ši plokštuma vadinama fazine plokštuma ir atspindi visų sistemos būsenų visumą. Taškas M(x,y) vadinamas reprezentuojančiu arba reprezentuojančiu tašku.

Įleisti pradžios momentas laiko t=t 0 reprezentuojančio taško koordinačių M 0 (x(t 0), y(t 0)). Kiekvieną kitą akimirką t reprezentacinis taškas pasislinks pagal kintamųjų verčių pokyčius x(t), y(t). Taškų rinkimas M(x(t), y (t)) fazinėje plokštumoje, kurios padėtis atitinka sistemos būsenas keičiantis kintamiesiems laikui bėgant x(t), y(t) pagal lygtis (4.1), vadinamas fazės trajektorija.

Visumą fazių trajektorijos skirtingoms pradinėms kintamųjų reikšmėms suteikia lengvai matomą sistemos „portretą“. Statyba fazinis portretas leidžia daryti išvadas apie kintamųjų pokyčių pobūdį x, y be žinios analitiniai sprendimai originali lygčių sistema(4.1).

Norint pavaizduoti fazinį portretą, kiekviename fazinės plokštumos taške būtina sukurti sistemos trajektorijų krypčių vektorinį lauką. Prieaugio nustatymasD t>0,gauname atitinkamus prieaugius D x Ir D y iš posakių:

D x=P(x,y)D t,

D y=Q(x,y)D t.

Vektorinė kryptis dy/dx taške ( x, y) priklauso nuo funkcijų ženklo P(x, y), Q(x, y) ir gali būti pateikta lentelė:

.(4.2)

Šios lygties sprendimas y = y(x, c), arba netiesiogiai F(x,y)=c, Kur Su– integravimo konstanta, pateikia lygties (4.2) integralų kreivių šeimą - fazių trajektorijos sistema (4.1) plokštumoje x, y.

Izoklininis metodas

Jie naudoja faziniam portretui sukurti izoklino metodas - fazinėje plokštumoje nubrėžiamos linijos, kurios kerta integralines kreives vienu konkrečiu kampu. Izoklininę lygtį galima lengvai gauti iš (4.2). Padėkime

Kur A– tam tikra pastovi vertė. Reikšmė A reiškia fazinės trajektorijos liestinės polinkio kampo liestinę ir gali gauti vertes nuo –¥ prie + ¥ . Vietoj to pakeičiama dy/dx(4.2) kiekis A gauname izoklininę lygtį:

.(4.3)

(4.3) lygtis kiekviename plokštumos taške apibrėžia unikalią atitinkamos integralinės kreivės liestinę, išskyrus tašką, kuriame P(x,y)= 0, Q (x,y) = 0 , kurioje liestinės kryptis tampa neapibrėžta, nes išvestinės vertė tampa neapibrėžta:

.

Šis taškas yra visų izoklinijų susikirtimo taškas - specialus taškas. Jame kintamųjų laiko išvestinės vienu metu išnyksta x Ir y.

Taigi viename taške kintamųjų kitimo greitis lygus nuliui. Vadinasi, fazių trajektorijų diferencialinių lygčių vienaskaitos taškas (4.2) atitinka stacionari sistemos būklė(4.1), o jo koordinatės yra stacionarios kintamųjų reikšmės x, y.

Ypatingą susidomėjimą kelia Pagrindinės izoklinos:

dy/dx=0, P(x,y)=0 – horizontaliųjų liestinių izoklinija ir

dy/dx=¥ ,Q(x,y)=0 – vertikalių liestinių izoklinija.

Sudarant pagrindines izoklines ir surandant jų susikirtimo tašką (x, y), kurių koordinatės atitinka sąlygas:

taip rasime visų fazinės plokštumos izoklinijų susikirtimo tašką, kuriame fazių trajektorijų liestinių kryptis yra neapibrėžta. tai - vienaskaitos taškas, kuris atitinka stacionari sistemos būklė(4.2 pav.).

Sistema (4.1) turi tiek stacionarių būsenų, kiek yra pagrindinių izoklinijų susikirtimo taškų fazinėje plokštumoje.

Kiekviena fazinė trajektorija atitinka aibę dinaminės sistemos judesių, einančių per tas pačias būsenas ir besiskiriančių viena nuo kitos tik laiko skaičiavimo pradžioje.

Jei įvykdytos Koši teoremos sąlygos, tai per kiekvieną erdvės tašką x, y, t yra tik viena integrali kreivė. Tas pats dėl savarankiškumo galioja ir fazinėms trajektorijoms: per kiekvieną fazės plokštumos tašką eina vienos fazės trajektorija.

Pastovios būsenos stabilumas

Tegul sistema būna pusiausvyros būsenoje.

Tada reprezentacinis taškas yra viename iš išskirtinių sistemos taškų, kuriame pagal apibrėžimą:

.

Ar vienaskaitos taškas yra stabilus, ar ne, nustatoma pagal tai, ar reprezentuojantis taškas išeina su nedideliu nuokrypiu nuo stacionarios būsenos. Kalbant apie dviejų lygčių sistemą, stabilumo apibrėžimas kalbojee, datrodo taip.

Pusiausvyros būsena yra stabili, jei esant bet kokiam nukrypimų nuo pusiausvyros būsenos diapazonui (e )galite nurodyti sritį d (e ), supantis pusiausvyros būseną ir turintis savybę, kad trajektorija neprasideda regione d , niekada nepasieks sienos e . (4.4 pav.)

Didelei sistemų klasei - grubios sistemos – kurių elgsenos pobūdis nesikeičia šiek tiek pasikeitus lygčių formai, informaciją apie elgsenos tipą šalia stacionarios būsenos galima gauti nagrinėjant ne pirminį, o supaprastintą tiesinis sistema.

Linijinės sistemos.

Apsvarstykite dviejų dalių sistemą tiesines lygtis:

.(4.4)

Čia a, b, c, d- konstantos, x, y- Dekarto koordinatės fazinėje plokštumoje.

Bendro sprendimo ieškosime formoje:

.(4.5)

Pakeiskime šias išraiškas į (4.4) ir sumažinkime iki e l t:

(4.6)

Algebrinė lygčių sistema (4.6) su nežinomaisiais A, B turi nulinį sprendimą tik tada, kai jo determinantas, sudarytas iš nežinomųjų koeficientų, yra lygus nuliui:

.

Išplėsdami šį determinantą, gauname būdingą sistemos lygtį:

.(4.7)

Išsprendus šią lygtį, gaunamos eksponentinės reikšmėsl 1,2 , kurioms galimos nulinės vertės A Ir B(4.6) lygties sprendiniai. Šios reikšmės yra

.(4.8)

Jei radikali išraiška yra neigiama, tadal 1,2 kompleksiniai konjuguoti skaičiai. Tarkime, kad abiejų (4.7) lygties šaknų tikrosios dalys nėra nulinės ir kad nėra kelių šaknų. Tada sistemos (4.4) bendrasis sprendimas gali būti pavaizduotas kaip tiesinis eksponentų ir eksponentų derinysl 1 , l 2 :

(4.9)

Norėdami išanalizuoti galimų sistemos trajektorijų fazinėje plokštumoje pobūdį, naudojame tiesinė vienalyčių koordinačių transformacija, kuri prives sistemą prie kanoninė forma:

,(4.10)

leidžianti patogesnį atvaizdavimą fazinėje plokštumoje lyginant su pradine sistema (4.4). Pristatome naujas koordinatesξ , η pagal formules:

(4.1)

Iš tiesinės algebros eigos žinoma, kad nelygybės atveju tikrosios dalys nulinėsl 1 , l 2 pradinė sistema (4.4) visada gali būti transformuota naudojant transformacijas (4.11) į kanoninę formą (4.10) ir galima ištirti jos elgesį fazinėje plokštumojeξ , η . Panagrinėkime įvairius atvejus, kurie čia gali pasirodyti.

Šaknys λ 1 , λ 2 – galiojantis ir to paties ženklo

Šiuo atveju transformacijos koeficientai yra realūs, mes judame iš tikrosios plokštumosx,yį tikrąją plokštumą ξ, η. Padalinę antrąją lygtį (4.10) iš pirmosios, gauname:

.(4.12)

Integravę šią lygtį, randame:

Kur .(4.13)

Sutikime suprasti λ 2 būdingos lygties šaknis su dideliu moduliu, kuri nepažeidžia mūsų samprotavimų bendrumo. Tada, kadangi nagrinėjamu atveju šaknys λ 1 , λ 2 – galiojantis ir to paties ženklo,a>1 , ir mes susiduriame su parabolinio tipo integralinėmis kreivėmis.

Visos integralinės kreivės (išskyrus ašį η , kuris atitinka ) prisilietimas prie ašies pradžios ξ, kuri kartu yra ir (4.11) lygties integralinė kreivė. Koordinačių pradžia yra ypatingas taškas.

Dabar išsiaiškinkime reprezentuojančio taško judėjimo kryptį fazinėmis trajektorijomis. Jei λ 1, λ 2 yra neigiami, tada, kaip matyti iš (4.10) lygčių, |ξ|, |η| laikui bėgant mažėti. Reprezentacinis taškas artėja prie koordinačių pradžios, bet niekada jo nepasiekia. Priešingu atveju tai prieštarautų Koši teoremai, teigiančiai, kad per kiekvieną fazės plokštumos tašką eina tik viena fazės trajektorija.

Toks ypatingas taškas, per kurį eina integralinės kreivės, kaip ir parabolių šeima eina per kilmę ir vadinamas mazgu (1 pav.). 4.5)

Mazgo tipo pusiausvyros būsena ties λ 1, λ 2 < 0 yra Lyapunov stabilus, nes reprezentacinis taškas juda visomis integralinėmis kreivėmis link koordinačių pradžios. Tai stabilus mazgas. Jei λ 1, λ 2 > 0, tada |ξ|, |η| laikui bėgant didėja, o reprezentacinis taškas nutolsta nuo koordinačių pradžios. Šiuo atveju specialus taškas– nestabilus mazgas .

Fazinėje plokštumoje x, y bus išsaugotas bendras kokybinis integralinių kreivių elgsenos pobūdis, tačiau integralinių kreivių liestinės nesutaps su koordinačių ašimis. Šių liestinių pasvirimo kampas bus nustatomas pagal koeficientų santykį α , β , γ , δ lygtyse (4.11).

Šaknys λ 1 , λ 2 – galioja ir skirtingų ženklų.

Konvertuoti iš koordinates x,y į koordinates ξ, η vėl tikra. Kanoninių kintamųjų lygtys vėl turi formą (4.10), bet dabar λ ženklai 1, λ 2 yra skirtingi. Fazių trajektorijų lygtis turi formą:

Kur , (4.14)

Integruodami (4.14), randame

(4.15)

Tai lygtis apibrėžia hiperbolinio tipo kreivių šeimą, kurioje yra abi koordinačių ašys– asimptotai (at a=1 turėtume lygiašonių hiperbolių šeimą). Koordinačių ašys šiuo atveju taip pat yra integralinės kreivės– tai bus vienintelės integralios kreivės, einančios per pradinį tašką. Kiekvienasiš kurių susideda iš trijų fazių trajektorijų: dviejų judesių į pusiausvyros būseną (arba iš pusiausvyros būsenos) ir iš pusiausvyros būsenos. Visos kitos integralinės kreivės– yra hiperbolės, kurios nepraeina per pradinę vietą (1 pav.). 4.6) Šis ypatingas taškas vadinamas "balnas ». Lygio linijos šalia kalno balno elgiasi panašiai kaip fazės trajektorijos šalia balno.

Panagrinėkime reprezentuojančio taško judėjimo fazinėmis trajektorijomis netoli pusiausvyros būsenos pobūdį. Tegu pvz.λ 1 > 0 , λ 2<0 . Tada reprezentacinis taškas dedamas ant ašies ξ , nutols nuo pradžios ir padėtas ant ašies η – neribotą laiką priartės prie koordinačių pradžios, nepasiekęs jo per ribotą laiką. Kur reprezentacinis taškas yra pradiniu momentu (išskyrus vienaskaitos tašką ir asimptotės taškus η =0), galiausiai jis nutols nuo pusiausvyros, net jei iš pradžių judės viena iš integralinių kreivių link vienaskaitos taško.

Tai akivaizdu atskiras taškas, pavyzdžiui, balnas, visada yra nestabilus . Tik specialiai parinktomis pradinėmis sąlygomis ties asimptoteη =0 sistema priartės prie pusiausvyros būsenos. Tačiau tai neprieštarauja teiginiui apie sistemos nestabilumą. Jei skaičiuosime, kad visos pradinės sistemos būsenos fazinėje plokštumoje yra vienodai tikėtinos, tada tokios pradinės būsenos, atitinkančios judėjimą kryptimi, tikimybėĮ vienaskaitos taškas lygus nuliui. Todėl bet koks tikras judėjimas pašalins sistemą iš pusiausvyros būsenos.Grįžtant prie koordinačiųx,y,gausime tokį pat kokybinį vaizdą apie trajektorijų judėjimo aplink koordinačių pradžią prigimtį.

Riba tarp nagrinėjamų mazgo ir balno atvejų yra atvejis Kada pavyzdžiui, vienas iš būdingų rodiklių λ 1 , išnyksta, o tai įvyksta, kai sistemos determinantas– išraiška ad-bc=0(žr. 4.8 formulę ). Šiuo atveju lygčių (4.4) dešiniųjų pusių koeficientai yra proporcingi vienas kitam:

o sistemos pusiausvyros būsenos yra visi tiesės taškai:

Likusios integralinės kreivės yra lygiagrečių tiesių linijų su kampiniu koeficientu šeima , pagal kurią reprezentuojantys taškai arba artėja prie pusiausvyros būsenos, arba tolsta nuo jos, priklausomai nuo charakteristikų lygties λ antrosios šaknies ženklo 2 = a+d.(4. 7 pav ) Šiuo atveju pusiausvyros būsenos koordinatės priklauso nuo pradinės kintamųjų reikšmės.

Šaknys λ 1 , λ 2 – kompleksaskonjugatas

Šiuo atveju tikraix Ir y mes padarysime turi sudėtingų konjugatų ξ , η (4.10) . Tačiau įvedant kitą tarpinę transformaciją, šiuo atveju taip pat galima svarstymą sumažinti iki tikrosios tiesinės vienalytės transformacijos. Padėkime:

(4.16)

Kur a,b, Ir u, v – faktines vertes. Galima parodyti, kad transformacija išx,yĮ u, v pagal mūsų prielaidas yra tikras, tiesinis, vienalytis su determinantu, kuris skiriasi nuo nulio. Dėl lygčių(4.10, 4.16) turime:

kur

(4.17)

Antrąją lygtį padalijus iš pirmosios, gauname:

kurią lengviau integruoti, jei einame į polinę koordinačių sistemą (r, φ ) . Po pakeitimo gauname iš kur:

.(4.18)

Taigi, fazinėje plokštumojeu, vmes susiduriame su logaritminių spiralių šeima, kurių kiekviena turiasimptotinis taškas pradinėje vietoje.Vienaskaitos taškas, kuris yra asimptotinis visų integralinių kreivių, turinčių spiralės formą, taškas, įdėtas į kiekvienądrauge, vadinasi sutelkti dėmesį ( 4.8 pav ) .

Panagrinėkime reprezentuojančio taško judėjimo fazinėmis trajektorijomis pobūdį. Pirmąją iš lygčių (4.17) padauginus išu, o antrasis įjungtas v ir pridėjus gauname:

Kur

Leiskite a 1 < 0 (a 1 = Reλ ) . Tada reprezentacinis taškas nuolat artėja prie koordinačių pradžios, nepasiekdamas jos per ribotą laiką. Tai reiškia, kad fazių trajektorijos yra besisukančios spiralės ir atitinka slopintus virpesius kintamieji. tai - pastovus dėmesys .

Stabilaus židinio atveju, kaip ir stabilaus mazgo atveju, tenkinama ne tik Lyapunov sąlyga, bet ir griežtesnis reikalavimas. Būtent, esant bet kokiems pradiniams nukrypimams, sistema laikui bėgant grįš taip arti pusiausvyros padėties, kiek norima. Toks stabilumas, kai pradiniai nuokrypiai ne tik nedidėja, bet ir mažėja, linkę į nulį, vadinamas absoliutus stabilumas .

Jei formulėje (4.18) a 1 >0 , tada reprezentacinis taškas nutolsta nuo pradžios, ir mes susiduriame su nestabilus dėmesys . Judant iš lėktuvou, vį fazinę plokštumąx, yspiralės taip pat liks spiralėmis, bet bus deformuotos.

Dabar panagrinėkime atvejį, kaia 1 =0 . Fazių trajektorijos lėktuveu, vbus apskritimai kuris lėktuvex,yatitinka elipses:

Taigi, kadaa 1=0 per specialų taškąx= 0, y= 0 jokia integrali kreivė nepraeina. Toks izoliuotas vienaskaitos taškas, šalia kurio integralinės kreivės yra uždaros kreivės, ypač elipsės, įterptos viena į kitą ir gaubiančios vienaskaitos tašką, vadinamas centru.

Taigi, priklausomai nuo charakteristikų lygties (4.7) šaknų pobūdžio, galimi šeši pusiausvyros būsenų tipai. Fazių trajektorijų vaizdas plokštumoje x, yšiems šešiems atvejams parodyta Fig. 4.9.

Ryžiai. 4.9.Tiesinių lygčių sistemos fazinių portretų tipai stacionarios būsenos apylinkėse (4.4).

Penkių tipų pusiausvyros būsenos yra grubios, jų pobūdis nesikeičia esant pakankamai mažiems pokyčiams dešiniosiose lygčių pusėse (4.4). Tokiu atveju pokyčiai ne tik dešiniosiose pusėse, bet ir jų pirmos eilės dariniuose turėtų būti nedideli. Šeštoji pusiausvyros būsena – centras – nėra grubi. Nežymiai pakeitus dešinės lygčių pusės parametrus, jis tampa stabiliu arba nestabiliu židiniu.

Bifurkacijos diagrama

Įveskime tokį užrašą:

. (4.11)

Tada charakteristikos lygtis bus parašyta taip:

. (4.12)

Apsvarstykite plokštumą su stačiakampėmis Dekarto koordinatėmis s , D ir pažymėkite ant jo sritis, atitinkančias vienokį ar kitokį pusiausvyros būsenos tipą, kurį lemia charakteristikos lygties šaknų pobūdis.

.(4.13)

Pusiausvyros būsenos stabilumo sąlyga bus neigiamos tikrosios y dalies buvimasl 1 ir l 2 . Tam būtina ir pakankama sąlyga yra nelygybių išsipildymass > 0, D > 0 . Diagramoje (4.15) ši sąlyga atitinka taškus, esančius pirmajame parametrų plokštumos ketvirtyje. Vienetinis taškas bus dėmesys, jeil 1 ir l 2 kompleksas. Ši sąlyga atitinka tuos plokštumos taškus, kuriems , tie. taškai tarp dviejų parabolės šakųs 2 = 4 D. Ašies taškai s = 0, D>0, atitinka centro tipo pusiausvyros būsenas. Lygiai taip patl 1 ir l 2 – yra galiojantys, tačiau skirtingų požymių, t.y. vienaskaitos taškas bus balnas, jei D<0, ir tt Rezultate gausime parametrų plokštumos skaidinio schemą s, D, į sritis, atitinkančias skirtingų tipų pusiausvyros būsenas.

Ryžiai. 4.10. Bifurkacijos diagrama

tiesinių lygčių sistemai 4.4

Jei tiesinės sistemos koeficientai a, b, c, d priklauso nuo tam tikro parametro, tada pasikeitus šiam parametrui reikšmės taip pat pasikeiss , D . Peržengus ribas kokybiškai pasikeičia fazinio portreto charakteris. Todėl tokios ribos vadinamos bifurkacinėmis ribomis – priešingose ​​ribos pusėse sistema turi du topologiškai skirtingus fazių portretus ir atitinkamai du skirtingus elgesio tipus.

Diagrama parodo, kaip tokie pokyčiai gali atsirasti. Jei atmesime ypatingus atvejus – koordinačių kilmę – tuomet nesunku pastebėti, kad kertant ordinačių ašį balnas gali transformuotis į mazgą, stabilų arba nestabilų. Stabilus mazgas gali patekti į balną arba į stabilų židinį ir pan. Atkreipkite dėmesį, kad perėjimai stabilus mazgas – stabilus židinys ir nestabilus mazgas – nestabilus židinys nėra bifurkacijos, nes fazių erdvės topologija nesikeičia. Plačiau apie fazių erdvės topologiją ir bifurkacijos perėjimus kalbėsime 6 paskaitoje.

Bifurkacijos perėjimų metu pasikeičia vienaskaitos taško stabilumo pobūdis. Pavyzdžiui, stabilus židinys per centrą gali virsti nestabiliu židiniu. Ši bifurkacija vadinama Andronovo-Hopfo bifurkacija jį tyrinėjusių mokslininkų vardais. Šios bifurkacijos metu netiesinėse sistemose gimsta ribinis ciklas, ir sistema tampa savaime svyruojančia (žr. 8 paskaitą).

Pavyzdys. Linijinė cheminių reakcijų sistema

Medžiaga X teka iš išorės pastoviu greičiu, virsta medžiaga Y ir greičiu, proporcingu medžiagos koncentracijai Y, pašalinamas iš reakcijos sferos. Visos reakcijos yra pirmos eilės, išskyrus medžiagų antplūdį iš išorės, kuris yra nulinės eilės. Reakcijos schema atrodo taip:

(4.14)

ir apibūdinama lygčių sistema:

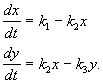(4.15)

Stacionarias koncentracijas gauname prilygindami dešiniąsias puses nuliui:

.(4.16)

Panagrinėkime sistemos fazės portretą. Antrąją sistemos (4.16) lygtį padalinkime iš pirmosios. Mes gauname:

.(4.17)

(4.17) lygtis nustato kintamųjų elgesį fazinėje plokštumoje. Sukurkime šios sistemos fazinį portretą. Pirmiausia nubrėžkime pagrindines izoklines fazinėje plokštumoje. Vertikalių liestinių izoklinijos lygtis:

Horizontaliųjų liestinių izoklinijos lygtis:

Vienaskaitos taškas (stacionari būsena) yra pagrindinių izoklinijų sankirtoje.

Dabar nustatykime, kokiu kampu koordinačių ašys susikerta su integralinėmis kreivėmis.

Jeigu x= 0, tada.

Taigi integralų kreivių liestinės liestinė y=y(x), kertantis ordinačių ašį x=0, yra neigiamas viršutinėje pusės plokštumoje (atminkite, kad kintamieji x, y turi koncentracijos vertes, todėl mus domina tik viršutinis dešinysis fazės plokštumos kvadrantas). Šiuo atveju liestinės kampo liestinė didėja didėjant atstumui nuo pradžios.

Apsvarstykite ašį y= 0. Taške, kur ši ašis kerta integralines kreives, jos apibūdinamos lygtimi

At integralinių kreivių, kertančių x ašį, nuolydžio liestinė yra teigiama ir didėja nuo nulio iki begalybės x.

Prie .

Tada, toliau didėjant, polinkio kampo liestinė absoliučia verte mažėja, lieka neigiama ir linkusi į -1 x ® ¥ . Žinant integralinių kreivių liestinių kryptį pagrindinėse izoklinijose ir koordinačių ašyse, nesunku sudaryti visą fazių trajektorijų vaizdą.

Lyapunov metodu nustatykime vienaskaitos taško stabilumo pobūdį. Būdingas sistemos determinantas turi tokią formą:

.

Išplėsdami determinantą, gauname būdingą sistemos lygtį: , t.y. Būdingos lygties šaknys yra neigiamos. Vadinasi, stacionari sistemos būsena yra stabilus mazgas. Šiuo atveju medžiagos koncentracija X linkęs į stacionarią būseną visada monotoniškai, medžiagos Y koncentracija gali praeiti per min arba max. Virpesių režimai tokioje sistemoje neįmanomi.

Pagrindinės sąvokos ir apibrėžimai:

Analitinės funkcijos f(z) nulis yra taškas „a“, kuriam f(a)=0.

Funkcijos f(z) „n“ eilės nulis yra taškas „a“, jei fn(a)¹0.

Vienaskaitos taškas „a“ vadinamas izoliuotu funkcijos f(z) vienaskaitos tašku, jei yra šio taško kaimynystė, kurioje nėra kitų vienaskaitos taškų, išskyrus „a“.

Yra trys izoliuotų vienaskaitos taškų tipai: .

1 nuimamas vienaskaitos taškas;

3 iš esmės pavieniai taškai.

Vienaskaitos taško tipą galima nustatyti remiantis duotosios funkcijos elgesiu rastame vienaskaitos taške, taip pat pagal Laurent'o eilės formą, gautą funkcijai šalia rasto vienaskaitos taško.

Vienaskaitos taško tipo nustatymas pagal funkcijos elgseną jame.

1. Nuimami vienaskaitos taškai.

Funkcijos f(z) izoliuotas vienaskaitos taškas a vadinamas nuimamu, jei yra baigtinė riba.

2.Lenkai.

Funkcijos f(z) izoliuotas vienaskaitos taškas a vadinamas poliu, jei .

3. Iš esmės vienaskaitos taškai.

Funkcijos f(z) izoliuotas vienaskaitos taškas a vadinamas iš esmės vienaskaitos tašku, jei neegzistuoja nei baigtinis, nei begalinis.

Tarp funkcijos nulių ir polių egzistuoja toks ryšys.

Kad taškas a būtų funkcijos f(Z) n eilės polius, būtina ir pakanka, kad šis taškas būtų funkcijos n eilės nulis.

Jei n=1 polius vadinamas paprastu.

Apibrėžimas: Atskiras vienareikšmio pobūdžio taškas vadinamas:

a) nuimamas, jei trūksta pagrindinės skaidymo dalies;

b) polius, jei pagrindinėje dalyje yra baigtinis terminų skaičius;

c) iš esmės vienaskaitos taškas, jei pagrindinėje dalyje yra begalinis skaičius narių.

a) Taigi, šalia nuimamo vienaskaitos taško, išplėtimas turi tokią formą:

ji išreiškia funkciją visuose apskritimo taškuose |z-a|

Centre z=a lygybė nėra teisinga, nes funkcija ties z=a turi nenutrūkstamumą, o dešinioji pusė yra ištisinė. Jei pakeičiama centre esančios funkcijos reikšmė, priimant ją lygią dešinės pusės reikšmei, tada tarpas bus pašalintas – iš čia ir pavadinimas – nuimamas.

b) Netoli m eilės poliaus Laurento serijos išplėtimas turi tokią formą:

c) Prie paprasto stulpo

Išskaičiavimai ir jų apskaičiavimo formulės.

Analitinės funkcijos f(z) liekana izoliuotame vienaskaitos taške z 0 yra kompleksinis skaičius, lygus integralo reikšmei , paimtas teigiama kryptimi išilgai apskritimo L, kurio centras yra taške z 0, esančiame funkcijos f(z) analitiškumo srityje (ty žiede 0<|z-z0|

Funkcijos f(z) liekana izoliuotame vienaskaitos taške z 0 žymima simboliu Res f(z 0) arba Res (f(z); z 0). Taigi,

Res f(z 0)= . (22.15.1)

Jei formulėje (22.15.1) įdėsime n=-1, gausime:

C -1 =

arba Res f(z 0) = C-1,

tie. funkcijos f(z) liekana vienaskaitos taško z 0 atžvilgiu yra lygi pirmojo nario koeficientui su neigiamu eksponentu funkcijos f(z) plėtinyje Laurent'o eilutėje.

Išskaitymų apskaičiavimas.

Įprasti arba nuimami pavieniai taškai. Akivaizdu, kad jei z=z 0 yra reguliarus arba nuimamas funkcijos f(z) vienaskaitos taškas, tai Res f(z 0)=0 (šiais atvejais Laurento plėtinyje trūksta pagrindinės dalies, todėl c-1=0) .

stulpas. Tegul taškas z 0 yra paprastas funkcijos f(z) polius. Tada funkcijos f(z) šalia taško z 0 Laurento serija yra tokia:

Iš čia

Todėl, perėję šią lygybę į ribą ties z --z 0, gauname

Res f(z0)=

Iš esmės ypatingas taškas. Jei taškas z 0 iš esmės yra funkcijos f(z) vienaskaitos taškas, tai norint apskaičiuoti funkcijos likutį šiame taške, dažniausiai tiesiogiai nustatomas koeficientas c-1 funkcijos Laurent'o eilėje.

Įvykių klasifikacija. Suma, įvykių sandauga, jų savybės, grafinis vaizdavimas.

Renginiai skirstomi į:

1. Atsitiktinis

2. Patikimas

3. Neįmanoma

Patikimas yra įvykis, kuris būtinai įvyksta tam tikromis sąlygomis (naktis po ryto).

Atsitiktinis įvykis – tai įvykis, kuris gali įvykti arba neįvykti (išlaikyti egzaminą).

Neįmanomas įvykis yra įvykis, kuris neįvyks tam tikromis sąlygomis (žalio pieštuko išėmimas iš dėžutės, kurioje yra tik raudoni).

Vienetinis taškas

matematikoje.

1) vienaskaitos kreivės taškas, apibrėžtas lygtimi F ( x, y) = 0, - taškas M 0 ( x 0, y 0), kuriame abi funkcijos F () dalinės išvestinės x, y) pereiti prie nulio:

Jei ne visos antrosios dalinės funkcijos F ( x, y) taške M 0 yra lygūs nuliui, tada O. t vadinama dviguba. Jei kartu su pirmosiomis išvestinėmis, išnykusiomis taške M0, išnyksta visos antrosios išvestinės, bet ne visos trečiosios išvestinės, tai lygtis vadinama triguba ir pan. Tiriant kreivės struktūrą šalia dvigubo O.t., išraiškos ženklas vaidina svarbų vaidmenį

Jei Δ > 0, tada atvira erdvė vadinama izoliuota; pavyzdžiui, ties kreive y 2 - x 4 + 4x 2= 0 koordinačių pradžia yra izoliuota O. t. ryžių. 1 ). Jei Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 - 4= 0 koordinačių pradžia yra mazgas O. t. ryžių. 2 ). Jei Δ = 0, tada bendras kreivės taškas yra izoliuotas arba jam būdinga tai, kad skirtingos kreivės atšakos šiame taške turi bendrą liestinę, pavyzdžiui: a) 1 tipo taškas - skirtingos kreivės atšakos. kreivės yra priešingose ​​bendros liestinės pusėse ir sudaro tašką, kaip kreivę y 2 - 3= 0 (žr ryžių. 3 ,a); b) 2 tipo taškas - skirtingos kreivės atšakos yra vienoje bendrosios liestinės pusėje, kaip kreivė (y – x 2)2–5= 0 (žr ryžių. 3 , b); c) savaiminio prisilietimo taškas (kreivei y 2 - 4= 0 pradžia yra prisilietimo prie savęs taškas; (cm. ryžių. 3 , V). Kartu su nurodytais O. t. yra daug kitų O. t. Pavyzdžiui, asimptotinis taškas yra spiralės su begaliniu posūkių skaičiumi viršūnė (žr. ryžių. 4 ), pabaigos taškas, kampinis taškas ir kt.

2) Diferencialinės lygties vienaskaitos taškas yra taškas, kuriame vienu metu išnyksta diferencialinės lygties dešinės pusės skaitiklis ir vardiklis (žr. Diferencialinės lygtys)

kur P ir Q yra nuolat diferencijuojamos funkcijos. Darant prielaidą, kad O. t yra koordinačių pradžioje ir naudojant Teiloro formulę (žr. Taylor formulę), (1) lygtį galime pavaizduoti formoje.

kur P 1 ( x, y) ir Q 1 ( x, y) – be galo mažas atžvilgiu

Būtent, jei λ 1 ≠ λ 2 ir λ 1 λ 2 > 0 arba λ 1 = λ 2, tai O. t yra mazgas. į jį patenka visos integralinės kreivės, einančios per taškus pakankamai mažoje mazgo kaimynystėje. Jei λ 1 ≠ λ 2 ir λ 1 λ 2 i β, α ≠ 0 ir β ≠ 0, tai bendras taškas yra židinys; visos integralios kreivės, einančios per taškus pakankamai mažoje židinio kaimynystėje, yra spiralės su begaliniu posūkių skaičiumi bet kurioje savavališkai mažoje židinio kaimynystėje. Jei galiausiai λ 1,2 = ± iβ, β ≠ 0, tada O pobūdis nėra nulemtas vien tiesiniais terminais P () plėtiniuose. x, y) ir Q ( x, y), kaip buvo visais aukščiau nurodytais atvejais; čia O. t. gali būti židinys arba centras, arba jis gali turėti sudėtingesnį pobūdį. Centro kaimynystėje visos integralios kreivės yra uždaros ir turi centrą savo viduje. Taigi, pavyzdžiui, taškas (0, 0) yra lygčių mazgas adresu" = 2u/x(λ 1 = 1, λ 2 = 2; žr ryžių. 5 , a) ir y" = u/x(λ 1 = λ 2 = 1; žr ryžių. 5 , b), lygties balnas y" = -y/x(λ 1 = -1, λ 2 = 1 ; cm. ryžių. 6 ), lygties židinys y" =(x + y) / (x - y) (λ 1 = 1 - i, λ 2 = 1 + i; cm. ryžių. 7 ) ir lygties centras y" = -x/y(λ 1 = -i, λ 2 = i; cm. ryžių. 8 ).

Jei x, y) ir Q ( x, y) analitinė, aukštesnės eilės O. t kaimynystė gali būti suskirstyta į sritis: D 1 - užpildyta integralinėmis kreivėmis, abu galai įtraukti į O. t (elipsines sritis), D 2 - užpildyti integralinėmis kreivėmis. vienas galas įtrauktas į O. t (parabolinės sritys), o D 3 - sritys, apribotos dviejų integralinių kreivių, įtrauktų į bendrąją teoriją, tarp kurių yra hiperbolės tipo integralinės kreivės (hiperbolinės sritys). ryžių. 9 ). Jei į orbitą t nėra įtrauktų integralinių kreivių, tada orbita t vadinama stabilaus tipo tašku. Stabilaus osciliatoriaus kaimynystę sudaro uždaros integralios kreivės, kuriose yra osmosas, tarp kurių yra spiralės (žr. ryžių. 10 ).

Diferencialinių lygčių tyrimas, t. y. iš esmės integralinių kreivių šeimų, esančių diferencialinių lygčių kaimynystėje, elgsenos tyrimas, yra viena iš kokybinės diferencialinių lygčių teorijos šakų ir atlieka svarbų vaidmenį taikymuose, ypač sprendžiant klausimus. judesio stabilumo (A. M. Lyapunov a, A. Poincare ir kt. darbai).

3) Vienvertės analitinės funkcijos vienaskaitos taškas yra taškas, kuriame pažeidžiamas funkcijos analitiškumas (žr. Analitinės funkcijos). Jeigu yra kaimynystė O. t. a, laisvas nuo kitų O. t., tada taškas A vadinamas izoliuotas O. t A- izoliuota bendroji tvarka ir egzistuoja baigtinė a, vadinama nuimama bendra forma. būtent darant prielaidą f(a)= b, tai įmanoma pasiekti a taps įprastu pataisytos funkcijos tašku. Pavyzdžiui, taškas z= 0 yra nuimamas O. t funkcijai f 1 (. z) = f(z), jei z≠ 0 ir f 1 (0), = 1, taškas z= 0 yra įprastas taškas [ f 1 (z) taške yra analitinis z= 0]. Jeigu A- izoliuotas O. t ir a vadinamas poliu arba neesminiu funkcijos tašku f(z), jei Laurent serija) veikia f(z) šalia izoliuoto O. t neturi neigiamų galių z - a, Jei A- nuimamas O. t., yra baigtinis neigiamų laipsnių skaičius z - a, Jei A- stulpas (šiuo atveju stulpo tvarka r apibrėžiamas kaip aukščiausias a laipsnis – iš esmės ypatingas taškas. Pavyzdžiui, dėl funkcijos

p = 2, 3, …)

taškas z= 0 yra eilės polius r, funkcijai

taškas z= 0 iš esmės yra vienaskaitos taškas.

Ant laipsnių eilutės konvergencijos apskritimo ribos turi būti bent vienas funkcijos, vaizduojamos šiame apskritime, O.t galios serija. Visi unikalios analitinės funkcijos (natūralios ribos) egzistavimo srities ribiniai taškai yra šios funkcijos ribos. Taigi visi vienetinio apskritimo taškai | z| = 1 yra ypatingi funkcijai

Daugiareikšmei analitinei funkcijai sąvoka „O. T." sunkiau. Be O. t., atskiruose funkcijos Riemann paviršiaus lapuose (tai yra vienareikšmių analitinių elementų O. t.) kiekvienas šakos taškas yra ir funkcijos O. t. Izoliuoti Riemann paviršiaus šakos taškai (tai yra tokie šakų taškai, kurių kai kuriose jų apylinkėse nėra jokių kitų O. t. funkcijų jokiame lape) klasifikuojami taip. Jei a yra izoliuotas baigtinės eilės šakos taškas ir yra baigtinis a, jis vadinamas kritiniu poliumi. Jeigu A- begalinės tvarkos izoliuotas šakos taškas ir a vadinamas transcendentiniu O.t. Visi kiti izoliuoti šakos taškai vadinami kritiniais iš esmės vienaskaitos taškais. Pavyzdžiai: taškas z= 0 yra įprastas kritinis funkcijos f ( z) = žurnalas z o funkcijos kritinis iš esmės vienaskaitinis taškas f (z) = sin ln z.

Kiekviena bendroji problema, išskyrus pašalinamą, yra kliūtis analitiniam tęstinumui, tai yra, analitinis tęsinys išilgai kreivės, einančios per neredukuojamą bendrąją problemą, yra neįmanomas.

Didžioji sovietinė enciklopedija. - M.: Tarybinė enciklopedija. 1969-1978 .

Pažiūrėkite, kas yra „vienaskaitos taškas“ kituose žodynuose:

Taškai čia. Taip pat žr. vienaskaitos tašką (diferencialinės lygtys). Matematikos bruožas arba singuliarumas yra taškas, kuriame matematinis objektas (dažniausiai funkcija) yra neapibrėžtas arba veikia netaisyklingai (pavyzdžiui, taškas, kuriame ... ... Vikipedija

Analitinė funkcija yra taškas, kuriame pažeidžiamos analitiškumo sąlygos. Jei analitinė funkcija f(z) pateikiama tam tikroje taško z0 kaimynystėje visur... Fizinė enciklopedija

Analitinė funkcija yra taškas, kuriame pažeidžiamas funkcijos analitiškumas... Didysis enciklopedinis žodynas

vienaskaitos taškas- - [Ja.N.Luginskis, M.S.Fezi Žilinskaja, Ju.S.Kabirovas. Anglų-rusų elektros inžinerijos ir energetikos žodynas, Maskva, 1999] Elektros inžinerijos temos, pagrindinės sąvokos EN vienaskaita ... Techninis vertėjo vadovas

1) Analitinė funkcija f(z) yra kliūtis kompleksinio kintamojo z funkcijos f(z) elemento analitiniam tęsimui tam tikru keliu šio kintamojo plokštumoje. Tegul analitinę funkciją f(z) apibrėžia kokia nors... ... Matematinė enciklopedija

Analitinė funkcija, taškas, kuriame pažeidžiamas funkcijos analitiškumas. * * * VIENAS TAŠKAS VIENAS analitinės funkcijos TAŠKAS, taškas, kuriame pažeidžiamas funkcijos analitiškumas... Enciklopedinis žodynas

vienaskaitos taškas- ypatingasis taškas statusas T sritis automatika atitikmenys: engl. vienaskaitos taškas vok. singularer Punkt, m rus. vienaskaitos taškas, f pranc. taškinė dalelė, m; point singulier, m … Automatikos terminalų žodynas

vienaskaitos taškas- ypatingasis taškas statusas T sritis fizika atitikmenys: engl. vienaskaitos taškas vok. singularer Punkt, m rus. vienaskaitos taškas, f pranc. point singulier, m … Fizikos terminų žodynas

Leiskite zq yra funkcijos /(r) vienaskaitos taškas, t.s. f(z) bet šiuo metu yra analitinis (ypač, jis gali būti neapibrėžtas). Jei yra tokia pradurta taško kaimynystė zq (t. y. aibė O z - zq f(z) yra aialitinis, tada zo paskambino izoliuotas vienaskaitos taškas funkcijas f(z).Šis apibrėžimas išlieka toks pat atveju zn = oo, jei jodas yra pradurtas taško kaimynystėje zq = oo suprasti rinkinį z> aš - apskritimo, kurio centras yra ištakoje, išorė. Kitaip tariant, ypatingas taškas zq yra izoliuotas, jei yra šio taško kaimynystė, kurioje yra kitų vienaskaitos taškų, išskyrus zq. Toliau nagrinėjame tik atskirus unikalaus pobūdžio taškus (funkciją f(z) laikoma vienareikšmiška).

Priklausomai nuo funkcijos elgesio f(z) adresu z -> zq Yra trijų tipų vienaskaitos taškai. Izoliuotas vienaskaitos taškas zq funkcijos f(z) vadinamas:

1) nuimamas vienaskaitos taškas, jei yra baigtinė riba

2) stulpas, jei yra riba

3) iš esmės ypatingas taškas, Jeigu f(z) neturi nei baigtinės, nei begalinės ribos ties z-> zq.

26.1 pavyzdys. Parodykime, kad visi trys vienaskaitos taškai yra realizuoti. Pasvarstykime f(z)= Taškas zq = 0 yra izoliuotas

ypatingas šios funkcijos taškas. Naudodami formulę (22.12), gauname išplėtimą

iš ko išplaukia, kad egzistuoja lim fi(z)= 1. Todėl zq = 0 yra

yra nuimamas funkcijos vienaskaitos taškas fi(z).

Funkcija f‘j(z) =--- turi stulpą taške zo= 1, nes

2 r„X

Dabar panagrinėkime funkciją )з(z)= e 1 ^ r ir parodykite tai zo = O iš esmės yra šios funkcijos vienaskaita. Kai stengiamasi z iki nulio išilgai tikrosios ašies kairės ir dešinės funkcijos /z ribos (z) skiriasi: lim Su 1 / 1 = 0, lim s 1 /* = os. Iš to išplaukia,

x->0-0 x->0+O

Ką f:i(z) neturi nei baigtinės, nei begalinės ribos ties 2 -> O tai yra. zq = O yra šios funkcijos vienaskaitos taškas. (Atkreipkite dėmesį, kad kaip esmė z - iy iki nulio išilgai įsivaizduojamos ašies funkcijos

neturi jokių apribojimų.)

Žinoma, yra neišskirtų vienaskaitos taškų. Pavyzdžiui. funkcija taškuose turi polius z n = -, n= ±1, ±2,...

Vadinasi, Zq = 0 yra neišskirtas šios funkcijos vienaskaitos taškas: bet kurioje (nesvarbu, kokioje mažoje) šio taško kaimynystėje yra kitų vienaskaitos taškų g p.

Leiskite zo- baigtinis izoliuotas funkcijos vienaskaitos taškas f(z). Tada f(z) yra panašus kai kuriose pradurtose 0 Zo taško apylinkėse zoši kaimynystė gali būti laikoma žiedu, kurio vidinis spindulys r = 0. Pagal 25.1 teoremą nagrinėjamoje kaimynystėje funkcija f(z) galima išplėsti į Laurent seriją (25.2). Parodysime, kad funkcijos elgsena 2 -> zq (ty vienaskaitos taško tipas zo) priklauso nuo pagrindinės išplėtimo dalies tipo (25.2); Ši aplinkybė paaiškina termino „pagrindinė dalis“ kilmę.

2G teorema.2. Funkcijos f(z) izoliuotas vienaskaitos taškas zo yra pašalinamas tada ir tik tuo atveju, jei Lorapovo plėtinys pradurtoje šio taško kaimynystėje turi oid

tie. susideda tik iš teisingos dalies, o visi pagrindinės dalies koeficientai lygūs kulkai.

Įrodymas. 1. Leiskite zo- nuimamas vienaskaitos taškas. Įrodykime, kad Laurento funkcijos išplėtimas f(z) turi formą (26.1). Nuo specialaus taško zo nuimamas, tada yra baigtinis riba lim f(z) = A. Vadinasi, f(z) yra ribojamas tam tikroje 0 z - zq taško pradurtoje kaimynystėje zo, tie. )(z) visiems z iš šios apylinkės. Imkime bet kurį r. U р /?| ir Laurent serijos koeficientams naudokite formules (25.3):

Pagrindinės plėtimosi dalies koeficientams n =- 1,-2,... Tokioms vertybėms n mes turime p~ p-e 0 val r-> 0. Kadangi vertė r gali būti pasirinktas savavališkai mažas, tada ponas ~" gali būti toks mažas, kiek norisi. Nuo |s t,| ^ Ponas ~ p ir c„ nepriklauso nuo p, tada c„ = 0 at Ir= - 1, -2,..., ką ir reikėjo įrodyti.

2. Tarkime, kad Laurent plėtinys turi formą (26.1). Serija (26.1) yra laipsnio serija ir. todėl susilieja ne tik pradurtoje vietoje, bet ir visoje apylinkėje z-zq įskaitant tašką zo; jo suma S(z) yra analitinis z ir S(z) = )(z) ties 0 z - zo R. Todėl yra ribota riba )(z)= Pt 5(g) = 5(th) – Todėl vienaskaitos taškas zq

Z->Zo Z-*Zo

nuimamas. Teorema įrodyta.

komentuoti. Iš teoremos įrodymo matyti, kad išimamo vienaskaitos taško pradurtoje kaimynystėje 0 z - zo funkcija f(z) sutampa su funkcija 5(r), kuri yra analitinė visoje kaimynystėje z - zo. Todėl, jei nustatome /(th) = S(zq), tada nekeičiant funkcijos reikšmių f(z) bet kuriuose pradurtos kaimynystės taškuose šią funkciją Go padarysime analitine, t.y. „Pašalinkime“ funkciją. Tai paaiškina terminą „nuimama funkcija“. Natūralu, kad tokie taškai yra reguliarūs, o ne vienetiniai funkcijos taškai f(z).

Apsvarstykite, pavyzdžiui, funkciją

26.1 pavyzdyje buvo parodyta, kad Pm Nr) = 1. t.y. vienaskaitos taškas

zq = 0 nuimamas. Nustatę /i(0) = 1, pašaliname singuliarumą ir gauname funkciją, kuri taške yra analitinė zq = 0 (ir visoje C plokštumoje).

Dabar apibūdinkime polius pagal Laurento išsiplėtimus.

26.3 teorema. Funkcijos f(z) izoliuotas vienaskaitos taškas Zo yra polius tada ir tik tada, kai pagrindinė Laurento plėtinio dalis su centru Zq turi tik baigtinį skaičių skirtingų

iš nulinių koeficientų su n:

Įrodymas. 1. Leiskite zq – polius, t.y. lim/( z) = oo.

Įrodykime, kad Laurento funkcijos išplėtimas f(z) turi formą (2G.2). Kadangi lim f(z)= oo. tada yra pradurta taško kaimynystė

ki zq. kuriame f(z) yra analitinis ir neturi nulių. Tada funkcija g(z) = 1 /f(z) taip pat bus analitinis šioje pradurtoje kaimynystėje, o lim g(z)= 0. Todėl Zo yra nuimamas *-? *0

funkcijos vienaskaitos taškas g(z). Apibrėžkime g(z) taške zo, dėjimas g(zo)= 0. Tada g(z) taps analitinis visoje (nepradurto) taško kaimynystėje z 0 , ir z 0 bus jos izoliuotas nulis. Pažymėkime pagal Nšio nulio dauginys (eilės). Kaip parodyta §23, taško kaimynystėje zq funkcija g(z) gali būti pavaizduotas formoje (žr. (23.2))

ir (z$) f 0 ir y>(z) yra analitinis tam tikroje taško kaimynystėje zo- Nes ip(z) ištisinis taške zo Ir g>(zo) Ф 0" tada ip(z) kai kuriose šio taško apylinkėse nėra nulių. Todėl 1 funkcija /-p(z) taip pat bus analitinis šioje kaimynystėje, todėl išplečiamas joje Taylor serijoje:

Atidarę skliaustus ir keisdami koeficientų pavadinimus, formoje rašome paskutinį išplėtimą

kur c_jv = 1>o f 0. Taigi pagrindinėje funkcijos /(r) Laurent išplėtimo dalyje yra tik baigtinis terminų skaičius; pasiekėme norimą lygybę (26.2).

2. Įsileiskite į pradurtą taškų kaimynystę th funkcija )(z) yra pavaizduotas Laurent plėtiniu (26.2) (išsamesnę formą žr. (26.3)), kurios pagrindinėje dalyje yra tik baigtinis terminų skaičius, ir Su- d" f 0. Būtina tai įrodyti Zq – funkcinis polius f(z). Lygybę (26,3) padauginus iš (G - G o) iV , gauname funkciją

(26.4) eilutė yra laipsnio eilutė, kuri susilieja į analitinę funkciją ne tik pradurtame taške, bet ir visoje taško kaimynystėje Zq. Todėl funkcija h(z) taps analitiškas šioje kaimynystėje, jei toliau jį apibrėžsime eidami įdėdami h(zo)= s_dg f 0. Tada

Taigi, taškas th yra polius, o 26.3 teorema yra įrodyta.

Nulinės funkcijos dauginys (tvarka). g(z)= 1//(g) vadinamas polių tvarka funkcija /(r). Jeigu N- th poliaus tvarka, tada g(z)= (g - Zo) N ip(z), ir (eik) F 0, ir, kaip parodyta 26.3 teoremos įrodymo pirmoje dalyje, funkcijos /(r) išplėtimas turi formą (26.3), kur c_/v f 0. Ir atvirkščiai, jei /(r) išplečiama į eilutę (26.3) ir e-i F 0, tada

t.s. N- funkcijos /(r) poliaus tvarka. Taigi, zq funkcijos polių tvarka/(G) yra lygus Laurent'o plėtimosi pagrindinės dalies didžiausio nenulinio koeficiento skaičiui pradurtoje taško zq kaimynystėje(t. y. lygus šiam skaičiui N, kas s_dg f 0 ir Sp= 0 at n > N).

Įrodykime tokį teiginį, kuris yra patogus programoms.

Išvada 26.4. Taškas zq yra N eilės polius/(G) tada ir tik tada/(G) atstovaujama formoje

čia h(z) yra analitinė funkcija, esanti netoli taško th ir h(zo) f 0.

Įrodymas. Funkcija cp(z) = l/h(z) yra analitinė kai kuriose taško h apylinkėse. 26.4 išvados sąlyga yra lygiavertė:

Štai kodėl zq - nulis daugybos N funkcijas g(z). taigi ir daugybos polius N funkcijos /(2).

II 26.5 pavyzdys. Raskite atskirtus funkcijos vienaskaitinius taškus ir nustatyti jų tipą.

Sprendimas: taškai, kuriuose (z 2 + 1 )(z+ Z) 2 = 0. Jei z 2 L- 1 = 0, tada 2 = ±g Jeigu (z 4-3) 2 = 0, tada z= -3. Todėl funkcija turi tris vienaskaitos taškus z= g, 22 = -g, Z3 = - 3. Apsvarstykite z:

G - pirmosios eilės stulpas (naudojome 26.4 išvadą). Panašiai galima įrodyti, kad 22 = -i taip pat pirmos eilės stulpas. 2z mes turime:

Pereikime prie iš esmės atskirų punktų.

26.6 teorema. Funkcijos f(z) izoliuotas vienaskaitos taškas zq iš esmės yra vienaskaita tada ir tik tada, kai pagrindinė Laurento plėtinio dalis, kurios centras yra zq, turi be galo daug skirtingų. nulis, koeficientai nuo p.

Įrodymas. 26.6 teorema tiesiogiai išplaukia iš 26.2 ir 26.3 teoremų. Iš tiesų, jei esmė zq iš esmės yra ypatingas, tada pagrindinės Laurent išplėtimo dalies negali nebūti arba gali būti baigtinis terminų skaičius (kitaip taškas Zq bus arba nuimamas, arba stulpelis). Todėl pagrindinėje dalyje terminų skaičius turi būti begalinis.

Ir atvirkščiai, jei pagrindinėje dalyje yra be galo daug terminų, tada Zq negali būti nei nuimamas taškas, nei stulpas. Iš to išplaukia, kad šis punktas iš esmės yra ypatingas.

Pagal apibrėžimą, iš esmės vienaskaitos taškas pasižymi tuo, kad funkcija /(2) neturi nei baigtinės, nei begalinės ribos. z ->zq. Išsamesnę idėją apie tai, kaip netaisyklinga yra funkcijos elgsena iš esmės vienaskaitos taško kaimynystėje, pateikia ši teorema.

26.7 teorema (Sokhotskio teorema). Jei zq yra būtinas asmenims, funkcijos f(z), tada bet kam kompleksinis skaičius L, įskaitant A = oi, yra tokia taškų z n seka, kad z n -> zo ir lim f(zn) = A.

p->os

Įrodymas. Pirmiausia panagrinėkime atvejį A = oo. Pirmoje 2G teoremos įrodymo dalyje.2 nustatėme, kad jeigu f(z) yra apribotas tam tikra taško r punkcija kaimynystėje, tada visi koeficientai c", n = - 1,- 2,... pagrindinės dalies yra lygūs nuliui (todėl singuliarumas eityje yra pašalinamas). Kadangi pagal sąlygą th yra esminis vienaskaitos taškas, tai bet kurioje punkto taško kaimynystėje funkcija f(r) yra neribota. Paimkime kokią nors stiprią kaimynystę 0 Z tokią, kad f(zi) > 1 (jei |/(r)| z - zo I/2 yra taškas z-2 , kuriame |/(yy)| > 2 ir tt: pradurtoje kaimynystėje O 71. Akivaizdu, kad r„ -e go ir lim /(r“) = oo. Taigi, jei A = oo, 26.7 teorema

įrodyta.

Leisk tai dabar A f oo. Pirmiausia darykime prielaidą, kad yra pradurta kaimynystė 0

= -yy---- bus analitiškas šioje pramuštoje kaimynystėje, todėl

/(G) - A

Vadinasi, go yra izoliuotas funkcijos Φ(r) vienaskaitos taškas. Mes jums parodysime. kad r yra iš esmės vienaskaitos Φ(r) taškas. Tai gali būti netiesa. Tada yra riba lim Ф(r), baigtinė arba begalinė. Kurį laiką

/(r) = A + , tada yra ir Hsh /(r), kuris prieštarauja sąlygai

F(g) ~ :-*z 0

Aš matau teoremą. Taigi r0 iš esmės yra funkcijos Φ(r) vienaskaita. Pagal tai, kas buvo įrodyta aukščiau, yra taškų r n seka, kad r n th ir lim Ф(r n) = oo. Iš čia

Mes įrodėme reikalingą teiginį darydami prielaidą, kad /(r) F A kurioje nors pradurtoje taško kaimynystėje eiti- Dabar manykime, kad tai klaidinga, t.y. bet kuriame savavališkai mažame pradurtame taško kaimynystėje yra toks taškas G", kad /(r") = L. Tada bet kuriam n pradurtoje kaimynystėje 0 f(z u) = А Taigi norimas teiginys yra teisingas n-juo

visais atvejais ir 26.7 teorema yra įrodyta.

Pagal 26.7 teoremą (Sokhotsky), bet kurioje (savavališkai mažoje) pradurtoje iš esmės vienaskaitos taško kaimynystėje funkcija /(r) paima reikšmes, kurios yra savavališkai artimos bet kuriam skaičiui iš išplėstinio taško. sudėtinga plokštuma SU.

Norint ištirti atskirtus vienaskaitos taškus, dažnai praverčia jau žinomi Teiloro pagrindinių elementariųjų funkcijų išplėtimai.

2G pavyzdys.8. Nustatykite funkcijos vienaskaitos taško tipą zq = 0

Išspręsta ir e. Išplėskime skaitiklį ir vardiklį į Taylor eilutę pakeičiant (22.11) 3 z vietoj r ir atėmus 1, gauname

Naudodamiesi (22.12), gauname vardiklio išplėtimą:

Šių išplėtimų serijos susilieja visoje kompleksinėje plokštumoje €. Turime

ir /2(2) yra anaritinės taško kaimynystėje zo = 0 (ir net visoje plokštumoje) ir /2 (20) F 0, tada h(z) taip pat yra analitinis kai kuriose taško gF 0 kaimynystėje. Pagal 26.4 išvadą taškas Zo = 0 yra eilės polius N=4.

II 26.9 pavyzdys. Raskite funkcijos vienaskaitinius taškus f(z)= sin j – ir nustatyti jų tipą.

R e in e i e Funkcija turi vieną baigtinį vienaskaitos tašką zq = 1. Kituose taškuose iš C funkcija w =--- analitinis; taigi funkcija sin w bus analitinis.

Pakeičiant - vietoj r į sinuso (22.12) plėtimą gauname

Gavome skilimą funkcijos nuodėmė- į Laurent'o eilutę, esančią pertrauktoje taško 2o = 1 kaimynystėje. Kadangi gautame išplėtime yra be galo daug neigiamų galių (r - 1), tada zq = 1 iš esmės yra vienaskaitos taškas (šiuo atveju Laurento plėtinį sudaro tik pagrindinė dalis, o taisyklingosios dalies nėra).

Atkreipkite dėmesį, kad singuliarumo pobūdį šiuo atveju buvo galima nustatyti tiesiogiai iš apibrėžimo, nesiimant serijos išplėtimo. Iš tiesų, yra sekos (r",) ir (2"), kurios susilieja zo= 1, ir toks f(z"n)= 1, /(2") = 0 (tokias sekas nurodykite patys). Taigi, f(z) neturi jokių apribojimų z -> 1 ir todėl taškas zq - 1 iš esmės yra ypatingas.

Supažindinkime su Laurento funkcijos išplėtimu taško kaimynystėje Zq = 00 ir apsvarstykite ryšį tarp plėtimosi ir singuliarumo pobūdžio šiame taške. Atkreipkite dėmesį, kad izoliuoto vienaskaitos taško ir jo tipo (nuimamas, polius arba iš esmės vienaskaitos) apibrėžimai perkeliami į atvejį zq = oc be pakeitimų. Bet teoremos 26.2. 26.3 ir 26.6, susijusius su Laurent plėtinių pobūdžiu, reikia pakeisti. Esmė ta, kad nariai cn(z- 2o) p. n= -1,-2,..., pagrindinė dalis, apibrėžianti funkcijos šalia „netaisyklingumą“. pabaigos taškas Zq, kadangi 2 linkę į oo, jie elgsis „teisingai“ (linkę į 0). Priešingai, teisingos dalies nariai su n= 1,2,... links oo; jie nustato požymio pobūdį Zq = oo. Todėl didžiąją plėtimosi dalį prie oo sudarys terminai su teigiamų galių p, o teisingas – su neigiamomis.

Įveskime naują kintamąjį w = 1/2. Funkcija tv = 1/2, išplėstas taip, kad u(oo) = 0, vienas su vienu ir atitinkamai nubrėžia apylinkes z > R taškų zq = 00 šalia |w| wq = 0. Jei funkcija f(z) analitika pradurtoje kaimynystėje R z Zq = oc, tada funkcija G(w) = f(l/w) bus analitinis didžiojoje kaimynystėje 0 wo = 0. Kadangi 2 -> oo bus w-> 0, tada

Štai kodėl G(w) turi taške wq = 0 yra to paties tipo kaip f(z) taške Zq = 00. Išplėskime funkciją G(w) į Laurent'o eilutę, esančią taško wo = 0 pradurtoje kaimynystėje:

Dešinėje (26.5) pusėje esančios sumos atitinka įprastą ir pagrindinę plėtimosi dalis. Pereikime prie kintamojo z, pakeičiant w = 1/z:

Paskyrimas n= -A*, 6* = 6_„ = s p ir tai pastebėjęs G(l/z) = f(z), gauname

Skilimas (2G.G) vadinamas Funkcijos f(z) Laurent'o išplėtimas taško zq pradurtoje kaimynystėje= oo. Pirmoji (2G.6) suma vadinama dešinę dalį, o antroji suma yra pagrindinė dalisšio skilimo. Kadangi šios sumos atitinka teisingas ir pagrindines išplėtimo dalis (26.5), tai išplėtimui (26.6) galioja 26.2, 26.3 ir 26.6 teoremų analogai. Taigi sekanti teorema bus 26.2 teoremos analogas.

26.10 teorema. Izoliuotas vienaskaitos taškasZq - OS (funkcijos/(G) yra pašalinamas tada ir tik tada, jei Laurent išplėtimas pradurtoje šio taško kaimynystėje turi formą

t.s. susideda tik iš teisingos dalies.

Įdėkime / (oo) = co. Funkcija, apibrėžta kaimynystėje susiliejančiomis serijomis (26.7). z > R taškas 2o = oc, vadinamas analitinis taške z o = oo. (Atkreipkite dėmesį, kad šis apibrėžimas atitinka funkcijos analitiškumą G(w) taške va = 0.)

26.11 pavyzdys. Ištirkite funkcijos vienaskaitos tašką zq = oo

Kadangi riba yra baigtinė, tada zo = oo yra nuimamas funkcijos /(r) vienaskaitos taškas. Jei įdėtume /(oo) = lim J(z)= 0, tada f(z) taps analitinis

tik taške Zo= os. Nurodykime, kaip rasti atitinkamą išplėtimą (26.7). Pereikime prie kintamojo w = 1 fz. Pakeičiant z= 1 /?е, gauname

(paskutinė lygybė galioja taško wо = 0 punkcinėje kaimynystėje, bet toliau apibrėšime (7(0) = 0). Gauta funkcija turi vienaskaitos taškus) w =± aš, w =-1/3, ir taške Wq = 0 yra analitinis. Išskleidimo funkcija G(w) pagal laipsnius w(kaip buvo padaryta 25.7 pavyzdyje) ir pakeičiant į gautas galių eilutes w = 1/z, galime gauti funkcijos išplėtimą (26.7). f(z).

26.3 teorema atvejui zo= oo bus perrašyta tokia forma.

26.12 teorema. Izoliuotas vienaskaitos taškas th = os funkcija f(z) yra polius tada ir tik tada, kai pagrindinė Laurento išplėtimo dalis (26.6) turi tik baigtinį skaičių nenulinių koeficientų Su":

Čia serija yra įprasta dalis, o daugianomas skliausteliuose yra pagrindinė išplėtimo dalis. Polių daugialypiškumas oc yra apibrėžiamas kaip polių dauginys wq = 0 funkcijų G(z). Nesunku pastebėti, kad stulpo dauginys sutampa su skaičiumi Nį (26.8).

Q p | (i 2 + 1) (z+3) 2

Užduotis. Parodykite, kad funkcija f(z) =-- -- turi

tašką zo = oo 3 eilės stulpas.

26.6 teorema dėl iš esmės vienaskaitos taško gali būti perrašyta tuo atveju zo= os beveik pažodžiui, ir mes apie tai išsamiai nekalbame.