Нууцлаг эмгэг: фракталуудын түүх ба тэдгээрийн хэрэглээний талбарууд. Анхны тоон дахь фракталууд

Танилцуулга

Фракталын тухай ойлголт................................................ ......................................................4

Фрактал үүссэн түүх ……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………6

Алгебрийн фракталууд……………………………………………….8

1. Малдебродын багц……………………………………………9

   Жулиа багц…………………………………………………11

   Ньютоны цөөрөмүүд (фракталууд)……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………13

   Фрактал (бөмбөлөг) Halley…………………………………………..14

Практик хэрэглээфракталууд……………………………………………………………………………………………………………………………………………………15

Дүгнэлт……………………………………………………………………………….19

Ашигласан материалын жагсаалт………………………………………………………………20

Танилцуулга

Шинжлэх ухааны хэл хурдацтай өөрчлөгдөж байна орчин үеийн ертөнц. Физикийн хөгжлийн түүх нэг зуун гаруй жилийн түүхтэй. Энэ хугацаанд асар олон янзын байгалийн үзэгдлүүдийг судалж, янз бүрийн туршилтын баримтуудыг тайлбарласан физикийн үндсэн хуулиудыг нээсэн.

Байгалийн ихэнх систем нь хоёр шинж чанарыг хослуулсан байдаг: нэгдүгээрт, тэдгээр нь маш том, ихэвчлэн олон талт, олон талт, нарийн төвөгтэй байдаг. хоёрдугаарттэд маш их нөлөөн дор үүсдэг Үгүй ээ их хэмжээнийэнгийн хэв маягийг бий болгож, эдгээр энгийн хэв маягийг дагаж, цаашид хөгжүүлнэ. Эдгээр нь хамгийн их юм өөр өөр системүүд, талстаас эхлээд энгийн бөөгнөрөл (үүлс, гол мөрөн, уулс, тив, одод гэх мэт янз бүрийн хуримтлалууд), экосистем болон биологийн объектууд(оймын навчнаас хүний ​​тархи). Фракталууд нь яг ийм объектууд юм: нэг талаас, нарийн төвөгтэй (хязгааргүй олон элемент агуулсан), нөгөө талаас, маш нарийн зааврын дагуу бүтээгдсэн. энгийн хуулиуд. Энэхүү өмчийн ачаар фракталууд нь байгалийн олон объекттой ижил төстэй байдаг. Гэхдээ фрактал нь нааштай харьцуулагддаг байгалийн объектФрактал нь математикийн хатуу тодорхойлолттой бөгөөд хатуу тодорхойлолт, дүн шинжилгээ хийх боломжийг олгодог. Тиймээс фракталуудын онол нь ургамлын үндэс системийн өсөлтийн хурд, намаг шавхах хөдөлмөрийн зардал, найлзууруудын өндрөөс сүрэл массын хамаарал болон бусад олон зүйлийг урьдчилан таамаглах боломжийг олгодог. Энэ бол математикийн шинэ чиглэл юм шинжлэх ухааны парадигмхарьцангуйн онолтой харьцуулж болохуйц хувьсгал ба квант механик. Фрактал геометрийн объектууд өөрийн гэсэн арга замаар гадаад төрхбидний дассан "ердийн" геометрийн хэлбэрүүдээс эрс ялгаатай. Үнэндээ энэ бол шинэ нээлт юм математик тайлбарУдаан хугацааны туршид ийм тайлбар өгөхгүй байсан системүүд.

Фрактал геометр нь "цэвэр" биш юм геометрийн онол. Энэ нь илүү ойлголт юм шинэ дүр төрхалдартай зүйлс дээр, ойлголтын бүтцийн өөрчлөлт, судлаачийг ертөнцийг шинэ байдлаар харахыг албаддаг.

Миний ажлын зорилго бол "фрактал" гэсэн ойлголт, түүний төрөл зүйл болох "алгебрийн фрактал" гэсэн ойлголттой танилцах явдал юм.

Фрактал ойлголт

Харьцангуй саяхан математикийн хувьд объектын дүрс гарч ирэв, илүү их хэмжээтэй, гэхдээ шугамтай төстэй. Зарим эрдэмтэд өргөнгүй шугам гэсэн ойлголттой эвлэрэхэд хэцүү байсан тул аажмаар судалж эхлэв. геометрийн хэлбэрүүдба бутархай орон зайн хэмжээс бүхий бүтэц. Бүх деривативтай тасралтгүй муруйнууд нь хугарсан эсвэл маш хазайсан муруйгаар солигдсон. Ийм муруйн тод жишээ бол Брауны бөөмийн замнал юм. Шинжлэх ухаанд фрактал гэсэн ойлголт ингэж бий болсон.

Фрактал(лат. fractus - буталсан, хугарсан, хугарсан) - цогц геометрийн дүрс, энэ нь өөрөө ижил төстэй шинж чанартай, өөрөөр хэлбэл хэд хэдэн хэсгээс бүрдэх бөгөөд тус бүр нь бүхэл бүтэн зурагтай төстэй (Зураг 1). Илүү их өргөн утгаарааФракталууд нь бутархай хэмжигдэхүүнтэй (Минковски эсвэл Хаусдорфын утгаараа) эсвэл хэмжигдэхүүнтэй Евклидийн орон зайн цэгүүдийн багц гэж ойлгогддог.

Цагаан будаа. 1
"Фрактал" гэдэг үг тийм биш гэдгийг тэмдэглэх нь зүйтэй математикийн нэр томъёомөн нийтээр хүлээн зөвшөөрөгдсөн хатуу чанд байдаггүй математикийн тодорхойлолт. Тухайн зураг нь дараах шинж чанаруудын аль нэгийг агуулсан тохиолдолд үүнийг ашиглаж болно.

Энэ нь бүх хэмжүүрээр өчүүхэн бус бүтэцтэй. Энэ нь ердийн тоонуудаас (тойрог, эллипс, график гэх мэт) ялгаатай юм жигд функц): Хэрэв бид ердийн дүрсийн жижиг хэлтэрхийг маш том хэмжээгээр харвал энэ нь шулуун шугамын хэлтэрхий мэт харагдах болно. Фракталын хувьд масштабыг нэмэгдүүлэх нь бүтцийг хялбарчлахад хүргэдэггүй;

Өөртэйгөө төстэй эсвэл ойролцоогоор өөртэйгөө төстэй.

Энэ нь бутархай хэмжигдэхүүнтэй.

Байгаль дээрх олон объектууд фрактал шинж чанартай байдаг, жишээлбэл, далайн эрэг, үүл, модны титэм, цусны эргэлтийн системмөн хүн, амьтны цулцангийн систем.
Фракталууд, ялангуяа онгоцонд, компьютер ашиглан бүтээхэд хялбар, гоо үзэсгэлэнг хослуулсан тул түгээмэл байдаг.

Фракталуудын түүх

19-20-р зууны эхэн үед фракталуудыг судлах нь системчилсэн гэхээсээ илүү үе шаттай байсан, учир нь өмнө нь математикчид голчлон судалж болох "сайн" объектуудыг судалдаг байв. нийтлэг аргуудба онолууд. 1872 онд Германы математикч Карл Вейерштрасс нэгэн жишээг бүтээжээ тасралтгүй функц, хаана ч ялгагдахгүй, өөрөөр хэлбэл аль ч цэг дээр шүргэгч байхгүй. Гэсэн хэдий ч түүний бүтэц нь бүхэлдээ хийсвэр бөгөөд ойлгоход хэцүү байв. Тиймээс 1904 онд Швед Хельге фон Кох хаана ч шүргэгчгүй, зурахад хялбар тасралтгүй муруйг гаргаж ирэв. Энэ нь фрактал шинж чанартай болох нь тогтоогдсон. Энэ муруйн нэг хувилбарыг "Кох цасан ширхгүүд" гэж нэрлэдэг.
Дүрүүдийн өөртэйгөө төстэй байх санааг Францын иргэн Пол Пьер Леви гаргасан. ирээдүйн зөвлөгчБенуа Манделброт. 1938 онд түүний "Хавтгай ба орон зайн муруй ба бүхэл хэсгүүдээс бүрдэх гадаргуу" нийтлэл хэвлэгдсэн бөгөөд энэ нь өөр нэг фрактал болох Леви С муруйг дүрсэлсэн юм. Дээр дурдсан бүх фракталуудыг конструктив (геометрийн) фракталуудын нэг анги гэж нөхцөлт байдлаар ангилж болно.
Өөр нэг анги бол динамик (алгебрийн) фракталууд бөгөөд үүнд Mandelbrot олонлог багтдаг. Энэ чиглэлийн анхны судалгаа нь 20-р зууны эхэн үеэс эхэлсэн бөгөөд нэрстэй холбоотой юм Францын математикчидГастон Жулиа, Пьер Фату нар. 1918 онд Жулиагийн бүтээл цогцолборын давталтаар хэвлэгджээ оновчтой функцуудМанделбротын багцтай нягт холбоотой фракталуудын бүхэл бүтэн гэр бүл болох Жулиа багцуудыг дүрсэлсэн. Энэ бүтээл нь шагнал хүртсэн Францын академиГэсэн хэдий ч энэ нь нэг ч дүрслэл агуулаагүй тул задгай объектын гоо үзэсгэлэнг үнэлэх боломжгүй байв.

Фрактал геометрийн анхны санаанууд 19-р зуунд үүссэн. Кантор энгийн рекурсив (давталт) процедурыг ашиглан шугамыг хоорондоо холбоогүй цэгүүдийн цуглуулга болгон хувиргасан (Кантор тоос гэж нэрлэдэг). Тэрээр нэг шугамыг авч, төвийн гуравны нэгийг хасаад дараа нь үлдсэн хэсгүүдтэй ижил зүйлийг давтана. (Зураг 2)

Цагаан будаа. 2

Пеано зурсан онцгой төрөлшугам.(Зураг 3)

Цагаан будаа. 3

Үүнийг зурахын тулд Пеано дараах алгоритмыг ашигласан.

Эхний алхамд тэрээр шулуун шугамыг авч, анхны шугамын уртаас 3 дахин богино 9 сегментээр сольсон (зургийн 1, 2-р хэсэг). Дараа нь тэр үүссэн шугамын сегмент бүртэй ижил зүйлийг хийв. Гэх мэтээр хязгааргүй. Шугамын өвөрмөц байдал нь бүхэл бүтэн хавтгайг дүүргэх явдал юм. Онгоцны цэг болгонд нэг цэг олддог нь батлагдсан шугаманд хамаарахПеано.

Пеаногийн муруй, Канторын тоос нь энгийн геометрийн объектуудаас давсан. Тэд тодорхой хэмжээсгүй байсан. Канторын тоос нь нэг хэмжээст шулуун шугамын үндсэн дээр баригдсан мэт боловч цэгүүдээс бүрддэг (хэмжээ 0). Мөн Peano муруй нь нэг хэмжээст шугамын үндсэн дээр баригдсан бөгөөд үр дүн нь хавтгай байв. Шинжлэх ухааны бусад олон салбарт асуудал гарч ирсэн бөгөөд тэдгээрийн шийдэл нь дээр дурдсантай төстэй хачирхалтай үр дүнд хүргэсэн ( Брауны хөдөлгөөн, хувьцааны үнэ).

20-р зуун хүртэл ийм мэдээлэл хачин объектууд, тэдгээрийг системчлэх ямар ч оролдлогогүйгээр. Орчин үеийн фрактал геометр, фрактал гэдэг үгийн эцэг Бенуа Мандельброт эдгээрийг эзэмших хүртэл тэр үе байсан. Баримтуудыг аажмаар харьцуулж үзээд тэрээр математикийн шинэ чиглэл болох фрактал геометрийг нээсэн юм.

Фракталыг илүү тодорхой төсөөлөхийн тулд Б.Манделбротын "Байгалийн фрактал геометр" номонд өгөгдсөн жишээг авч үзье, энэ нь сонгодог болсон "Британийн эргийн урт хэд вэ?" Энэ асуултын хариулт нь санагдсан шиг энгийн биш юм. Энэ бүхэн ашигласан хэрэгслийн уртаас хамаарна. Эргийг километрийн захирагч ашиглан хэмжсэнээр тэд тодорхой хэмжээний урттай болдог. Гэсэн хэдий ч хэмжсэн захирагчаас хамаагүй бага хэмжээтэй олон жижиг булан, хойгуудыг орхигдуулж байна. Захирагчийн хэмжээг 1 метр болгон бууруулснаар эргийн урт уртасна. Миллиметрийн захирагч ашиглан банкны уртыг хэмжихдээ нэг миллиметрээс том хэсгүүдийг харгалзан үзвэл урт нь бүр ч их байх болно. Үүний үр дүнд ийм энгийн мэт асуултын хариулт нь хэнийг ч гайхшруулж чадна - Британийн эргийн урт нь төгсгөлгүй юм.

Алгебрийн фракталууд

Алгебрийн фракталууд нь үндсэн дээр бүтээгдсэн тул нэрээ авсан алгебрийн томъёо. Алгебрийн фракталуудыг олж авах хэд хэдэн арга байдаг. Аргын нэг нь функцийг дахин дахин тооцоолох явдал юм, хаанаz - нийлмэл тоо, ба f нь тодорхой функц юм. Энэ функцийг тооцоолох нь тодорхой нөхцөлийг биелүүлэх хүртэл үргэлжилнэ. Мөн энэ нөхцөл хангагдсан тохиолдолд дэлгэцэн дээр цэг гарч ирнэ. Энэ тохиолдолд функцийн утгууд нь өөр өөр цэгүүд нарийн төвөгтэй хавтгайбайж болно өөр өөр зан байдал:

цаг хугацааны явцад хязгааргүй болох хандлагатай байдаг;

0 хандлагатай;
хэд хэдэн тогтмол утгыг авдаг бөгөөд тэдгээрээс хэтрэхгүй;
зан байдал ямар ч чиг хандлагагүй эмх замбараагүй байдаг.

3.1 Манделбротын багц

Манделбротын багцыг (хамгийн алдартай фрактал объектуудын нэг) Бенуа Манделброт 1980 оны хавар анх (компьютер ашиглан) бүтээжээ. судалгааны төвнэрээр нэрлэгдсэн IBM компани. Томас Ж.Уотсон. Хэдийгээр ийм объектын судалгаа өнгөрсөн зуунд эхэлсэн ч энэ багцыг нээж, техник хангамжийг сайжруулсан явдал юм. компьютерийн графикВ шийдвэрлэх зэрэгфрактал геометр, эмх замбараагүй байдлын онолын хөгжилд нөлөөлсөн. Тэгэхээр, Mandelbrot багц гэж юу вэ?

Комплекс хувьсагчийн функцийг авч үзье. тавьямөн дарааллыг анхаарч үзээрэй, хаана нь. Ийм дарааллыг хязгаарлаж болно (өөрөөр хэлбэл ямар ч гэсэн r байж болно) эсвэл "хязгааргүйд зугтах" (жишээ нь r > 0 байгаа тохиолдолд). Манделбротын олонлогийг заасан дараалал нь хязгаарлагдсан c цогц тоонуудын багц гэж тодорхойлж болно. Харамсалтай нь энэ нь мэдэгдэхгүй байна аналитик илэрхийлэл, энэ нь өгөгдсөн c нь Манделбротын олонлогт хамаарах эсэхийг тодорхойлох боломжийг олгоно. Тиймээс багцыг бий болгохын тулд компьютерийн туршилтыг ашигладаг: тэд нарийн төвөгтэй хавтгай дээрх багц цэгүүдийг тодорхой алхамаар хардаг бөгөөд цэг бүрийг гүйцэтгэдэг. тодорхой тоодавталт (дарааллын тодорхой тооны гишүүдийг ол) ба түүний "зан байдлыг" ажигла. (Зураг 4).

Манделбротын олонлог нь r=2 радиустай тойрогт төв нь эх дээр байрладаг нь батлагдсан. Тиймээс, хэрэв ямар нэгэн алхамд дарааллын дараагийн гишүүний модуль 2-оос хэтэрвэл энэ дарааллыг тодорхойлсон c-д харгалзах цэг нь Манделбротын олонлогт хамаарахгүй гэж шууд дүгнэж болно.

Комплекс тоонуудын сканнердах үе шатыг багасгаж, давталтын тоог нэмэгдүүлснээр бид хүссэн хэмжээгээрээ нарийвчилсан мэдээллийг авах боломжтой, гэхдээ үргэлж зөвхөн багцын ойролцоо зургийг авах боломжтой.

0-ээс N-1 хүртэл тодорхой тоогоор дугаарласан N өнгө бидэнд байг. Бид дахин тодорхой байхын тулд хар өнгө нь 0 тоотой гэж таамаглах болно. Хэрэв N-1 давталтын дараа өгөгдсөн c-ийн хувьд цэг нь 2 радиустай тойргоос хэтэрч чадахгүй бол бид c нь Манделбротын олонлогт харьяалагддаг гэж үзээд энэ цэгийг будна. в хар. Үгүй бол, хэрэв k (k Є ) алхам дээр дараагийн цэг нь 2 радиустай тойргийн гадна гарсан бол (өөрөөр хэлбэл k-р алхам дээр бид үүнийг "зугтсан" гэдгийг ойлгосон) бид үүнийг k өнгөөр ​​будна.

Үзэсгэлэнтэй зургуудыг хэзээ олж авдаг сайн сонголтбагцын палитр ба хөршүүд (жишээлбэл, багцын гадна бид "өнгөт цэгүүд" авах болно) (Зураг 5, 6).

Цагаан будаа. 4

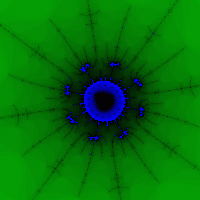
Цагаан будаа. 5 Зураг. 6

3.2 Жулиа багц

Манделбротын багцтай нягт холбоотой Жулиа багцыг 20-р зууны эхээр математикч Гастон Жулиа, Пьер Фату нар судалжээ (үзнэ үү). 1917-1919 онд Тэд нийлмэл хувьсагчийн функцүүдийн давталттай холбоотой үндсэн үр дүнг олж авсан. Ерөнхийдөө энэ баримтыг тусдаа хэлэлцэх нь зүйтэй бөгөөд гайхалтай жишээ юм математикийн судалгаа, цаг хугацаанаасаа олон арван жилийн өмнө (эрдэмтэд тэдний судалж байсан объектууд ямар байсныг зөвхөн төсөөлж байсан!), гэхдээ бид зөвхөн нийлмэл хувьсагчийн функцэд зориулж Жулиа олонлог байгуулах аргыг тайлбарлах болно.. Илүү нарийн яривал бид гэгчийг бүтээнэ. "Жулиа багцыг дүүргэх".

Тэгш өнцөгтийг авч үзье (x 1 ;y 1 )-(x 2 ;y 2 ). Тогтмол c-г засч, сонгосон тэгш өнцөгтийн цэгүүдийг тодорхой алхамаар харж эхэлье. Манделбротын олонлогийг бүтээхтэй адил цэг бүрийн хувьд бид хэд хэдэн давталт хийдэг (хаас илүү их тоодавталт хийх тусам багцыг илүү нарийвчлалтай авах болно). Хэрэв хэд хэдэн давталтын дараа цэг нь 2-р радиустай тойргийн хилээс "зугтахгүй" бол бид үүнийг хар өнгөөр, эс тэгвээс палитраас өнгөөр ​​будна. (Зураг 7, 8, 9, 10).

Цагаан будаа. 7

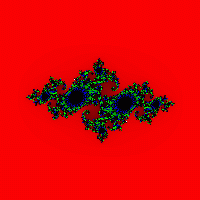
Зураг.8 Зураг. 9

Цагаан будаа. 10

3.3 Ньютоны усан сан (фрактал)

Динамик фракталуудын өөр нэг төрөл нь Ньютоны фракталууд (сав газар гэж нэрлэгддэг) юм. (Зураг 11). Тэдний барилгын томъёо нь шийдлийн арга дээр суурилдаг шугаман бус тэгшитгэл 17-р зуунд агуу математикч зохион бүтээсэн. Өргөдөл гаргаж байна ерөнхий томъёоНьютоны арга zn+1 = zn - f (zn)/f"(zn), n=0, 1, 2... zk-a олон гишүүнт f (x)=0 тэгшитгэлийг шийдэхийн тулд бид цэгүүдийн дарааллыг олж авна. : zn+1 = (k-1)znk/kznk-1, n=0, 1, 2... Анхны ойролцоолсон z0-ийн янз бүрийн комплекс тоонуудыг сонгосноор бид түүнээс хойш энэ олон гишүүнтийн язгуурт нийлэх дарааллыг олж авна яг k үндэстэй, дараа нь бүх хавтгай нь k хэсэгт хуваагдана - эдгээр хэсгүүдийн хил хязгаар нь фрактал бүтэцтэй байдаг.

Цагаан будаа. 11

3.4 Фрактал (бөмбөлөг) Халлей

Динамик фрактал байгуулах дүрмийн дагуу функцийн язгуурын ойролцоо утгыг олохын тулд Галлейгийн томъёог ашигладаг бол ийм фракталуудыг олж авна. (Зураг 12).

Арга нь давталтын дарааллаас бүрдэнэ.

Аргын санаа нь динамик фрактал зурахад ашигладагтай бараг ижил байна: бид заримыг нь авдаг анхны утга(ердийнх шигээ бид ярьж байна хувьсагч ба функцуудын утгууд) ба томъёог олон удаа хэрэглэж, тоонуудын дарааллыг олж авна. Энэ нь бараг үргэлж функцийн тэгүүдийн аль нэгэнд нийлдэг (өөрөөр хэлбэл функц 0 утгыг авах хувьсагчийн утга). Хэллигийн арга нь төвөгтэй томъёог үл харгалзан үр дүнтэй байдаг аргаас илүү үр дүнтэй : Дараалал нь тэг функц руу илүү хурдан нийлдэг.

Цагаан будаа. 12

Фракталуудын практик хэрэглээ

Фракталууд бүгдийг олдог илүү өргөн хэрэглээшинжлэх ухаанд. Үүний гол шалтгаан нь тэдгээрийг дүрсэлсэн явдал юм бодит ертөнцзаримдаа уламжлалт физик, математикаас ч илүү байдаг. Зарим жишээг энд оруулав.

Компьютерийн системүүд

Компьютерийн бүтээж чадах бүх зургуудаас цөөхөн нь фрактал зургуудтай өрсөлдөх чадвартай байдаг бид ярьж байнажинхэнэ гоо сайхны тухай.

Ихэнх ашигтай хэрэглээКомпьютерийн шинжлэх ухаан дахь фракталууд нь фрактал өгөгдлийг шахах явдал юм. Энэ төрлийн шахалт нь бодит ертөнцийг фрактал геометрээр сайн дүрсэлсэнд суурилдаг. Үүний зэрэгцээ зургууд нь ердийн аргуудыг (jpeg эсвэл gif гэх мэт) хийснээс хамаагүй сайн шахдаг. Фрактал шахалтын өөр нэг давуу тал нь зургийг томруулсан үед пикселийн эффект байхгүй (цэгүүдийн хэмжээг томруулж, зургийг гажуудуулдаг хэмжээсүүд) юм. Фрактал шахалтын тусламжтайгаар томруулсаны дараа зураг өмнөхөөсөө илүү сайхан харагддаг.

Шингэний механик

Урсгал дахь турбулентийн судалгаа нь маш сайн зохицсон байдаг

фракталууд. Турбулент урсгал нь эмх замбараагүй байдаг тул үнэн зөв загварчлахад хэцүү байдаг. Энд фрактал дүрслэл рүү шилжих нь инженер, физикчдийн ажлыг ихээхэн хөнгөвчлөхөд тусалдаг бөгөөд энэ нь нарийн төвөгтэй урсгалын динамикийг илүү сайн ойлгох боломжийг олгодог.

Фракталуудыг ашигласнаар та дөлийг дуурайж болно.

Сүвэрхэг материал нь маш нарийн төвөгтэй геометртэй тул фрактал хэлбэрээр сайн дүрслэгдсэн байдаг. Үүнийг газрын тосны шинжлэх ухаанд ашигладаг.

Харилцаа холбоо

Холын зайд өгөгдөл дамжуулахын тулд антенууд

фрактал хэлбэрүүд нь тэдний хэмжээ, жинг ихээхэн бууруулдаг. Фракталуудыг гадаргуугийн муруйлтыг тодорхойлоход ашигладаг. Тэгш бус гадаргуу нь хоёр өөр фракталын хослолоор тодорхойлогддог.
Эм

Био мэдрэхүйн харилцан үйлчлэл. Зүрхний цохилт.
Биологи

Эмх замбараагүй үйл явцын загварчлал, ялангуяа популяцийн загварыг тайлбарлахдаа.
Нанотехнологи

Нанотехнологийн хувьд фракталууд бас үүрэг гүйцэтгэдэг чухал үүрэгӨөрөө шаталсан зохион байгуулалттай учраас олон нано системүүд нь бүхэл бус хэмжээстэй байдаг, өөрөөр хэлбэл тэдгээр нь геометрийн, физик-химийн эсвэл функциональ шинж чанараараа фракталууд юм. Жишээ нь, тод жишээХимийн фрактал системүүд нь молекулууд "дендромерууд » . (Зураг 13)

Цагаан будаа. 13

Уран зохиол

дунд уран зохиолын бүтээлүүдТекст, бүтцийн эсвэл семантик фрактал шинж чанартай зүйлийг олох. Текстийн фракталуудад текстийн элементүүд эцэс төгсгөлгүй давтагдах боломжтой (“Тахилч нохойтой байжээ...”, “Өөрийгөө эрвээхэй гэж мөрөөдөж буй гүн ухаантны сургаалт зүйрлэл. болон өргөтгөлтэй бичвэрүүд (“Түүний Жак барьсан байшин”)

Бүтцийн фракталуудад текстийн схем нь фрактал байж болно: сонетуудын хэлхээ (15 шүлэг), сонетуудын хэлхээ (211 шүлэг), сонетуудын хэлхээ (2455 шүлэг).

Дүгнэлт

Фрактал бол хязгааргүй нарийн төвөгтэй объект бөгөөд түүний олон нарийн ширийн зүйлийг холоос ч ойроос харах боломжийг олгодог. Дэлхий - сонгодог жишээфрактал объект. Сансраас харахад бөмбөг шиг харагдаж байна. Түүнд ойртвол далай, тив, далайн эрэг, нурууг олж харах болно. Уулсыг илүү ойроос харцгаая - бүр нарийн ширийн зүйлс харагдах болно: уулын гадаргуу дээрх хэсэг газар, цар хүрээ нь уул шиг нарийн төвөгтэй, тэгш бус байдаг. Бүр илүү томруулж чадвал хөрсний жижиг хэсгүүд илрэх бөгөөд тэдгээр нь өөрөө фрактал объект юм.

Эцэст нь хэлэхэд, фракталууд нээгдсэний дараа Евклидийн геометрийн хуучин сайн хэлбэрүүд нь зарим нэг жигд бус байдал, эмх замбараагүй байдал, урьдчилан таамаглах боломжгүй байдгаас ихэнх байгалийн объектуудаас хамаагүй доогуур байдаг нь олон эрдэмтдэд илэрхий болсон гэдгийг хэлмээр байна. Фрактал геометрийн шинэ санаа нь олон зүйлийг судлахад туслах болно нууцлаг үзэгдлүүд хүрээлэн буй байгаль. Одоогийн байдлаар фракталууд физик, биологи, анагаах ухаан, социологи, эдийн засгийн олон салбарт хурдацтай нэвтэрч байна. Шинэ үзэл баримтлалыг ашигладаг зураг боловсруулах, хэв маягийг таних аргууд нь судлаачдад энэхүү математикийн төхөөрөмжийг ашиглах боломжийг олгодог. тоон тодорхойлолт асар их хэмжээбайгалийн объект, бүтэц.

Ашигласан уран зохиолын жагсаалт

1. Фракталуудын танилцуулга,

2. Zhikov V.V. Julia багц дээр. // Орчин үеийн байгалийн шинжлэх ухаан: Нэвтэрхий толь: 10 боть Т.1: Математик. Механик. М., 2000 он.

3. Жиков В.В. Фракталууд. // Орчин үеийн байгалийн шинжлэх ухаан: Нэвтэрхий толь: 10 боть Т.1: Математик. Механик. М., 2000 он.

4. Манделброт Б. Байгалийн фрактал геометр. – М: Компьютерийн судалгааны хүрээлэн, 2002 он.

5. Морозов А.Д. Фракталын онолын танилцуулга - Москва-Ижевск: Компьютерийн судалгааны хүрээлэн, 2002, 160 хуудас.

6. Динамик (алгебрийн) фракталууд // Элементүүд.. URL:http:// энгийн. ru/ зурагт хуудас/ фракталууд/ динамик

7. Динамик (алгебрийн) фракталууд // Элементүүд.. URL:http:// elementy.ru/posters/fractals/Mandelbrot#nop

8. Алгебрийн фракталууд // Фракталууд.. URL:http://rusproject.narod.ru/article/fractals.htm

Мэдээжийн хэрэг эрвээхэй могойн талаар юу ч мэдэхгүй. Гэхдээ эрвээхэй агнадаг шувууд тэдний тухай мэддэг. Могойг сайн таньдаггүй шувууд...

(Динамик) фракталууд

Энэ төрлийн фракталууд нь шугаман бус динамик системийг судлах үед үүсдэг (иймээс нэр). Ийм системийн зан үйлийг цогцолбороор дүрсэлж болно шугаман бус функц(олон гишүүнт) f(z). Нарийн төвөгтэй хавтгай дээрх анхны z0 цэгийг авч үзье. Одоо нийлмэл хавтгай дээрх тоонуудын төгсгөлгүй дарааллыг авч үзье, тэдгээр нь тус бүрийг өмнөх нэгээс нь олж авсан: z0, z1 = f(z0), z2 = f(z1), ... zn+1 = f(zn). -аас хамаарна эхлэх цэг z0 ийм дараалал нь өөрөөр ажиллах боломжтой: n → ∞ гэж хязгааргүйд хандах; заримтай нь нийлэх төгсгөлийн цэг; тогтмол утгуудын цувралыг циклээр авах; Илүү төвөгтэй сонголтууд бас боломжтой.

Иймд нийлмэл хавтгайн ямар ч z цэг нь f(z) функцийн давталтын үед өөрийн гэсэн зан төлөвтэй байх ба бүх хавтгай хэсэг хэсгүүдэд хуваагдана. Түүнээс гадна эдгээр хэсгүүдийн хил дээр байрлах цэгүүд нь дараахь шинж чанартай байдаг: дур зоргоороо бага нүүлгэн шилжүүлэлт хийснээр тэдний зан төлөвийн шинж чанар эрс өөрчлөгддөг (ийм цэгүүдийг салаалсан цэг гэж нэрлэдэг). Тиймээс, нэг төрлийн зан төлөвтэй цэгүүдийн багц, түүнчлэн салаалсан цэгүүдийн багц нь ихэвчлэн фрактал шинж чанартай байдаг. Эдгээр нь f(z) функцийн Жулиа олонлогууд юм.

Mandelbrot багц нь арай өөрөөр бүтээгдсэн. fc(z) = z2 + c функцийг авч үзье, энд c нь комплекс тоо. Энэ функцийн дарааллыг z0 = 0-тэй байгуулъя, энэ нь c параметрээс хамааран хязгааргүйд хуваагдах эсвэл хязгаарлагдмал хэвээр үлдэж болно. Түүнчлэн, энэ дараалал хязгаарлагдмал c-ийн бүх утгууд нь Манделбротын багцаас бүрдэнэ. Үүнийг Манделброт өөрөө болон бусад математикчид нарийвчлан судалж, олон зүйлийг нээсэн сонирхолтой шинж чанаруудэнэ олон хүнээс.

Жулиа, Манделбротын багцын тодорхойлолтууд хоорондоо төстэй байгааг харж болно. Үнэндээ эдгээр хоёр багц нь хоорондоо нягт холбоотой. Тухайлбал, Манделбротын багц нь Julia олонлог fc(z) холбогдсон c цогц параметрийн бүх утгууд юм (зарим нэмэлт нөхцлөөр хоёр салангид хэсэгт хуваагдах боломжгүй бол үүнийг холбогдсон гэж нэрлэдэг).

Энэ бол хамгийн их том бүлэгфракталууд. Тэдгээрийг шугаман бус процессуудыг ашиглан олж авдаг n хэмжээст орон зай. Хоёр хэмжээст процессууд хамгийн их судлагдсан байдаг. Шугаман бус давталтын процессыг салангид динамик систем гэж тайлбарлахдаа эдгээр системийн онолын нэр томъёог ашиглаж болно: фазын хөрөг, тогтвортой төлөвийн процесс, татагч гэх мэт.

Шугаман бус динамик системүүд хэд хэдэн тогтвортой төлөвтэй байдаг нь мэдэгдэж байна. Динамик систем тодорхой тооны давталтын дараа өөрийгөө олох төлөв нь түүний анхны төлөвөөс хамаарна. Тиймээс тогтвортой төлөв бүр (эсвэл тэдний хэлснээр татагч) нь анхны төлөвүүдийн тодорхой мужтай байдаг бөгөөд үүнээс систем нь авч үзэж буй эцсийн төлөвт орох болно. Тиймээс фазын орон зайсистем нь татагчдыг татах хэсэгт хуваагддаг. Хэрэв фазын орон зай нь хоёр хэмжээст байвал таталцлын хэсгүүдийг будна өөр өөр өнгө, та энэ системийн өнгөт фазын хөрөг зургийг авах боломжтой (давталтын процесс). Өнгө сонгох алгоритмыг өөрчилснөөр та хачирхалтай олон өнгийн хээ бүхий нарийн төвөгтэй фрактал хэв маягийг авах боломжтой. Математикчдын хувьд гэнэтийн зүйл бол анхдагч алгоритмуудыг ашиглан маш нарийн төвөгтэй бус бүтцийг бий болгох чадвар байв.

Жишээ болгон Mandelbrot багцыг авч үзье (Зураг 3 ба 4-р зургийг үз). Үүнийг бүтээх алгоритм нь маш энгийн бөгөөд энгийн давталтын илэрхийлэл дээр суурилдаг:

Z = Z[i] * Z[i] + C,

Энд Zi ба C нь нийлмэл хувьсагч юм. Давталтуудыг тэгш өнцөгт буюу дөрвөлжин бүсийн С эхлэх цэг бүрт гүйцэтгэдэг - цогц хавтгайн дэд хэсэг. Давталт үйл явц нь Z[i] нь 2 радиустай тойргоос гарах хүртэл үргэлжилнэ, түүний төв нь (0,0) цэг дээр байрладаг (энэ нь татагч гэсэн үг юм. динамик системхязгааргүйд байна), эсвэл хангалттай дараа их тоодавталт (жишээ нь 200-500) Z[i] тойргийн аль нэг цэгт нийлнэ. Z[i] тойрог дотор үлдсэн давталтын тооноос хамааран та C цэгийн өнгийг тохируулж болно (хэрэв Z[i] хангалттай олон тооны давталтаар тойрог дотор хэвээр байвал давталтын процесс зогсох бөгөөд энэ растер цэгийг хараар будсан).

Дээрх алгоритм нь Mandelbrot олонлог гэж нэрлэгддэг ойролцоо утгыг өгдөг. Mandelbrot багц цэгүүдийг агуулсан, үед хязгааргүй тоодавталт нь хязгааргүйд хүрдэггүй (цэгүүд нь хар өнгөтэй). Олонлогийн заагт хамаарах цэгүүд (энэ нь нарийн төвөгтэй бүтэц) хязгааргүйд оч эцсийн тоодавталт, олонлогоос гадуур байрлах цэгүүд хэд хэдэн давталтын дараа хязгааргүйд очдог (цагаан дэвсгэр).

Алгебрийн фракталуудын жишээ:

• Манделбротын багц
• Жулиа тавилаа
• Халлейн фрактал
• Ньютоны фрактал

Би энэ фракталыг голын гадаргуу дээрх долгионы интерференцийг харж байхдаа олж мэдсэн. Долгион нь эрэг рүү хөдөлж, тусгалаа олж, өөр дээрээ наалддаг. Долгион бий болгодог хэв маягт дэг журам байдаг уу? Түүнийг олохыг хичээцгээе. Долгионыг бүхэлд нь биш, зөвхөн түүний хөдөлгөөний векторыг авч үзье. Туршилтыг хялбарчлахын тулд "эрэг" -ийг жигд болгоцгооё.

Туршилтыг сургуулийн дэвтэр дээрх ердийн цаасан дээр хийж болно.

Эсвэл алгоритмын JavaScript хэрэгжилтийг ашиглах.

q ба p талуудтай тэгш өнцөгтийг авъя. Булангаас булан руу туяа (вектор) илгээцгээе. Цацраг нь тэгш өнцөгтийн нэг тал руу шилжиж, тусгалаа олж, дараагийн тал руу шилжинэ. Энэ нь цацраг нь үлдсэн булангуудын аль нэгэнд хүрэх хүртэл үргэлжилнэ. Хэрэв q ба p талуудын хэмжээ нь харьцангуй анхны тоонууд бол хэв маягийг олж авна (бид дараа нь үзэх болно - фрактал).

Зураг дээр бид энэ алгоритм хэрхэн ажилладагийг тодорхой харж болно.

Gif хөдөлгөөнт дүрс:

Хамгийн гайхалтай нь тэр нь өөр өөр талуудтэгш өнцөгт - бид өөр өөр хэв маягийг олж авдаг.

Би яагаад эдгээр хэв маягийг фрактал гэж нэрлэдэг вэ? Та бүхний мэдэж байгаагаар "фрактал" гэдэг нь өөрөө ижил төстэй шинж чанартай геометрийн дүрс юм. Зургийн нэг хэсэг нь зургийг бүхэлд нь давтана. Хэрэв та Q ба P талуудын хэмжээсийг мэдэгдэхүйц нэмэгдүүлэх юм бол эдгээр хэв маяг нь өөрөө ижил төстэй шинж чанартай байх нь тодорхой байна.

Үүнийг нэмэгдүүлэхийг хичээцгээе. Бид үүнийг зальтай аргаар нэмэгдүүлэх болно. Жишээ нь 17x29 загварыг авч үзье. Дараах загварууд нь: 29x(17+29=46), 46x(29+46=75)…
Нэг тал: F(n);
Хоёр дахь тал: F(n+1)=F(n)+F(n-1);
17, 29, 46, 75, 121, 196, 317, 513, 830, 1343
Фибоначчийн тоонуудын адил зөвхөн дарааллын эхний болон хоёр дахь гишүүд нь ялгаатай: F(0)=17, F(1)=29.

Хэрэв том талтэр ч байтугай үр дүн нь дараах загвар юм.

Хэрэв богино тал нь тэгш байвал:

Хэрэв хоёр тал нь сондгой байвал бид тэгш хэмтэй хэв маягийг олж авна.

Цацраг хэрхэн эхлэхээс хамаарч:

эсвэл

Би эдгээр тэгш өнцөгтүүдэд юу болж байгааг тайлбарлахыг хичээх болно.

Талбайг тэгш өнцөгтөөс салгаж, хил дээр юу болохыг харцгаая.

Цацраг нь орж ирсэн тэр цэгээс гарна.

Үүний зэрэгцээ туяа дамжин өнгөрөх квадратуудын тоо үргэлж тэгш тоо байдаг.

Тиймээс, хэрэв та тэгш өнцөгтөөс квадратыг таслах юм бол фракталын өөрчлөгдөөгүй хэсэг үлдэх болно.

Хэрэв та квадратуудыг фракталаас аль болох олон удаа салгавал фракталын "эхлэлд" хүрч болно.

Энэ нь Фибоначчийн спираль шиг харагдаж байна уу?

Фракталуудыг мөн Фибоначчийн тооноос авч болно.

Математикийн хувьд Фибоначчийн тоонууд (Фибоначчийн цуврал, Фибоначчийн дараалал) нь дараах тоонууд юм.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597…
Тодорхойлолтоор Фибоначчийн дарааллын эхний хоёр цифр нь 0 ба 1 бөгөөд дараагийн тоо бүр нь өмнөх хоёрын нийлбэртэй тэнцүү байна.
F(n)=F(n-1)+F(n-2)
F(0)=0, F(1)=1

Явцгаая:

Бидний харж байгаагаар талуудын харьцаа нь алтан харьцаанд ойртох тусам фракталын нарийвчлал ихсэх болно.

Энэ тохиолдолд фрактал нь фракталын хэсгийг давтаж, -ээр нэмэгддэг.

Фибоначчийн тоонуудын оронд та үндэслэлгүй хажуугийн хэмжээг ашиглаж болно:

Бид ижил фрактал авдаг.

Хэрэв та цацрагийг өөр өнцгөөр харвал ижил фракталуудыг квадратаас авах боломжтой.

Дүгнэж хэлэхэд та юу хэлэх вэ?
Эмх замбараагүй байдал нь бас дэг журам юм. Өөрийн гэсэн хуультай. Энэ тушаалыг судлаагүй боловч судлахад нэлээд тохиромжтой. Шинжлэх ухааны бүхий л хүсэл бол эдгээр хэв маягийг нээх явдал юм. Эцэст нь том дүр зургийг харахын тулд тааварын хэсгүүдийг холбоно.
Голын гадаргууг харцгаая. Хэрэв та чулуу шидвэл долгион ирнэ. Суралцах боломжтой дугуйлангууд. Хурд, хугацаа, долгионы урт - энэ бүгдийг тооцоолж болно. Гэвч давалгаа эрэгт хүрэх хүртэл тусгалгүй, давхцаж эхэлдэг. Бид эмх замбараагүй байдлыг (хөндлөнгөөс) авдаг бөгөөд үүнийг судлахад аль хэдийн хэцүү байдаг.
Хэрэв бид эсрэг чиглэлээс хөдөлвөл яах вэ? Долгионы зан үйлийг аль болох хялбарчлах. Хялбаршуулж, загвараа олж, дараа нь тайлбарлахыг хичээ бүрэн зурагюу болоод байна.
Юуг хялбарчилж болох вэ? Мэдээжийн хэрэг, цацруулагч гадаргууг гулзайлгахгүйгээр шулуун болго. Дараа нь долгионы оронд зөвхөн долгионы хөдөлгөөний векторыг ашиглана. Зарчмын хувьд энэ нь энгийн алгоритмыг бий болгож, процессыг компьютер дээр дуурайхад хангалттай юм. Энгийн алаг цаасан дээр долгионы зан үйлийн "загвар" хийхэд хангалттай.
Үүний үр дүнд бидэнд юу байна вэ? Үүний үр дүнд бид үүнийг харж байна долгионы процессууд(голын гадаргуу дээрх ижил долгионууд) бидэнд эмх замбараагүй байдал биш, харин бие биенийхээ дээр байрлах фракталууд (өөрөө ижил төстэй бүтэц) байдаг.

Өөр төрлийн долгионыг авч үзье. Мэдэгдэж байгаагаар, цахилгаан соронзон долгиондолгионы вектор ба цахилгаан ба хүчдэлийн вектор гэсэн гурван вектороос бүрдэнэ соронзон орон. Бидний харж байгаагаар хэрэв та ийм давалгааг "барьж" байвал хаалттай талбай- Эдгээр векторууд огтлолцох үед бид маш тодорхой хаалттай бүтэцтэй болно. Магадгүй энгийн бөөмс- Эдгээр нь ижил фракталууд мөн үү?

1-ээс 80 (6723x6723 px) хүртэлх тэгш өнцөгт дэх бүх фракталууд:

Фрактал дахь хаалттай хэсгүүд (6723x6723 пиксел):

Зүгээр л сайхан фрактал (4078x2518 пиксел):