Trigonometrinių lygčių šaknų nustatymas. Trigonometrinės lygtys

Norėdami sėkmingai išspręsti trigonometrines lygtis patogus naudoti mažinimo metodasį anksčiau išspręstas problemas. Išsiaiškinkime, kokia yra šio metodo esmė?

Bet kurioje siūlomoje užduotyje turite pamatyti anksčiau išspręstą problemą, o tada naudoti iš eilės lygiavertės transformacijos pasistenkite sumažinti jums duotą užduotį į paprastesnę.

Taigi, sprendžiant trigonometrines lygtis paprastai siekia kai kuriuos baigtinė seka lygiavertės lygtys, kurių paskutinė grandis yra lygtis su akivaizdžiu sprendiniu. Tik svarbu atsiminti, kad jei nesuformuos paprasčiausių trigonometrinių lygčių sprendimo įgūdžių, tada sprendimas yra daugiau sudėtingos lygtys bus sunku ir neveiksminga.

Be to, spręsdami trigonometrines lygtis niekada neturėtumėte pamiršti, kad yra keli galimi sprendimo būdai.

1 pavyzdys. Raskite šaknų skaičių cos lygtys x = -1/2 intervale .

Sprendimas:

I metodas Nubraižykime funkcijas y = cos x ir y = -1/2 ir raskime jų bendrų taškų skaičių intervale (1 pav.).

Kadangi funkcijų grafikai turi du bendrų taškų intervale , tada lygtyje yra dvi šio intervalo šaknys.

II metodas. Naudodami trigonometrinį apskritimą (2 pav.) sužinome taškų skaičių priklausantis intervalui, kuriame cos x = -1/2. Paveikslėlyje parodyta, kad lygtis turi dvi šaknis.

III metodas. Naudodami trigonometrinės lygties šaknų formulę, išsprendžiame lygtį cos x = -1/2.

x = ± arccos (-1/2) + 2πk, k – sveikas skaičius (k € Z);

x = ± (π – arccos 1/2) + 2πk, k – sveikas skaičius (k € Z);

x = ± (π – π/3) + 2πk, k – sveikas skaičius (k € Z);

x = ± 2π/3 + 2πk, k – sveikas skaičius (k € Z).

Intervale yra šaknys 2π/3 ir -2π/3 + 2π, k yra sveikasis skaičius. Taigi lygtis turi dvi šaknis tam tikrame intervale.

Atsakymas: 2.

Ateityje trigonometrinės lygtys bus sprendžiamos vienu iš siūlomų metodų, o tai daugeliu atvejų neatmeta kitų metodų naudojimo.

2 pavyzdys. Raskite lygties tg (x + π/4) = 1 sprendinių skaičių intervale [-2π; 2π].

Sprendimas:

Naudodami trigonometrinės lygties šaknų formulę, gauname:

x + π/4 = arctan 1 + πk, k – sveikas skaičius (k € Z);

x + π/4 = π/4 + πk, k – sveikas skaičius (k € Z);

x = πk, k – sveikas skaičius (k € Z);

Intervalas [-2π; 2π] priklauso skaičiams -2π; -π; 0; π; 2π. Taigi, lygtis turi penkias šaknis tam tikrame intervale.

Atsakymas: 5.

3 pavyzdys. Raskite lygties cos 2 x + sin x · cos x = 1 šaknų skaičių intervale [-π; π].

Sprendimas:

Kadangi 1 = sin 2 x + cos 2 x (pagrindinis trigonometrinė tapatybė), tada pradinė lygtis įgauna tokią formą:

cos 2 x + sin x · cos x = sin 2 x + cos 2 x;

sin 2 x – sin x cos x = 0;

sin x(sin x – cos x) = 0. sandauga lygi nuliui, o tai reiškia, kad bent vienas iš veiksnių turi būti lygus nuliui, Štai kodėl:

sin x = 0 arba sin x – cos x = 0.

Kadangi kintamojo, kuriame cos x = 0, reikšmės nėra antrosios lygties šaknys (to paties skaičiaus sinusas ir kosinusas vienu metu negali būti lygūs nuliui), padalijame abi antrosios lygties puses pagal cos x:

sin x = 0 arba sin x / cos x - 1 = 0.

Antroje lygtyje naudojame faktą, kad tg x = sin x / cos x, tada:

sin x = 0 arba tan x = 1. Naudodami formules turime:

x = πk arba x = π/4 + πk, k – sveikas skaičius (k € Z).

Nuo pirmosios šaknų serijos iki intervalo [-π; π] priklauso skaičiams -π; 0; π. Iš antrosios serijos: (π/4 – π) ir π/4.

Taigi yra penkios šaknys pradinė lygtis priklauso intervalui [-π; π].

Atsakymas: 5.

4 pavyzdys. Raskite lygties tg 2 x + сtg 2 x + 3tg x + 3сtgx + 4 = 0 šaknų sumą intervale [-π; 1,1π].

Sprendimas:

Perrašykime lygtį taip:

tg 2 x + сtg 2 x + 3(tg x + сtgx) + 4 = 0 ir pakeiskite.

Tegu tg x + сtgx = a. Padėkime abi lygties puses kvadratu:

(tg x + сtg x) 2 = a 2. Išplėskime skliaustus:

tg 2 x + 2tg x · сtgx + сtg 2 x = a 2.

Kadangi tg x · сtgx = 1, tai tg 2 x + 2 + сtg 2 x = a 2, o tai reiškia

tg 2 x + сtg 2 x = a 2 – 2.

Dabar pradinė lygtis atrodo taip:

a 2 – 2 + 3a + 4 = 0;

a 2 + 3a + 2 = 0. Naudodamiesi Vietos teorema, nustatome, kad a = -1 arba a = -2.

Atlikime atvirkštinį pakeitimą, turime:

tg x + сtgx = -1 arba tg x + сtgx = -2. Išspręskime gautas lygtis.

tg x + 1/tgx = -1 arba tg x + 1/tgx = -2.

Pagal jųdviejų turtą jie yra abipusiai abipusiai skaičiai nustatome, kad pirmoji lygtis neturi šaknų, o iš antrosios lygties turime:

tg x = -1, t.y. x = -π/4 + πk, k – sveikas skaičius (k € Z).

Intervalas [-π; 1,1π] priklauso šaknims: -π/4; -π/4 + π. Jų suma:

-π/4 + (-π/4 + π) = -π/2 + π = π/2.

Atsakymas: π/2.

5 pavyzdys. Raskite vidurkį aritmetinės šaknys nuodėmės lygtys 3x + sin x = sin 2x intervale [-π; 0,5π].

Sprendimas:

Pasinaudokime formulė nuodėmėα + sin β = 2sin ((α + β)/2) cos ((α – β)/2), tada

sin 3x + sin x = 2sin ((3x + x)/2) cos ((3x – x)/2) = 2sin 2x cos x ir lygtis tampa

2sin 2x cos x = sin 2x;

2sin 2x · cos x – sin 2x = 0. Išimkime bendras daugiklis sin 2x iš skliaustų

sin 2x(2cos x – 1) = 0. Išspręskite gautą lygtį:

sin 2x = 0 arba 2cos x – 1 = 0;

sin 2x = 0 arba cos x = 1/2;

2x = πk arba x = ±π/3 + 2πk, k – sveikas skaičius (k € Z).

Taigi mes turime šaknis

x = πk/2, x = π/3 + 2πk, x = -π/3 + 2πk, k – sveikas skaičius (k € Z).

Intervalas [-π; 0,5π] priklauso šaknims -π; -π/2; 0; π/2 (iš pirmosios šaknų serijos); π/3 (iš antrosios serijos); -π/3 (iš trečios serijos). Jų aritmetinis vidurkis:

(-π – π/2 + 0 + π/2 + π/3 – π/3)/6 = -π/6.

Atsakymas: -π/6.

6 pavyzdys. Raskite lygties sin x + cos x = 0 šaknų skaičių intervale [-1,25π; 2π].

Sprendimas:

Ši lygtis yra vienalytė pirmojo laipsnio lygtis. Abi jo dalis padalinkime iš cosx (kintamojo, kuriame cos x = 0 reikšmė nėra šaknys duota lygtis, nes to paties skaičiaus sinusas ir kosinusas vienu metu negali būti lygūs nuliui). Pradinė lygtis yra tokia:

x = -π/4 + πk, k – sveikas skaičius (k € Z).

Intervalas [-1,25π; 2π] priklauso šaknims -π/4; (-π/4 + π); ir (-π/4 + 2π).

Taigi duotame intervale yra trys lygties šaknys.

Atsakymas: 3.

Išmokite atlikti svarbiausią dalyką – aiškiai įsivaizduokite problemos sprendimo planą, tada bet kokia trigonometrinė lygtis bus jūsų rankose.

Vis dar turite klausimų? Nežinote, kaip išspręsti trigonometrines lygtis?
Norėdami gauti pagalbos iš dėstytojo, užsiregistruokite.

svetainėje, kopijuojant visą medžiagą ar jos dalį, būtina nuoroda į šaltinį.

Galite užsisakyti detalus sprendimas tavo užduotis!!!

Lygybė, kurioje po ženklu yra nežinomasis trigonometrinė funkcija(„sin x, cos x, tan x“ arba „ctg x“) vadinama trigonometrine lygtimi, todėl toliau nagrinėsime jų formules.

Paprasčiausios lygtys vadinamos „sin x=a, cos x=a, tg x=a, ctg x=a“, kur „x“ yra kampas, kurį reikia rasti, „a“ yra bet koks skaičius. Užrašykime kiekvienos iš jų šaknies formules.

1. Lygtis „sin x=a“.

„|a|>1“ sprendimų nėra.

Kai `|a| \leq 1` turi begalinis skaičius sprendimus.

Šakninė formulė: `x=(-1)^n arcsin a + \pi n, n \in Z`

2. Lygtis „cos x=a“.

Jei `|a|>1` – kaip ir sinuso atveju, sprendiniai tarp realūs skaičiai neturi.

Kai `|a| \leq 1` turi begalinis rinkinys sprendimus.

Šakninė formulė: `x=\pm arccos a + 2\pi n, n \in Z`

Specialūs sinuso ir kosinuso atvejai diagramose.

3. Lygtis „tg x=a“.

Turi begalinį bet kokių „a“ reikšmių sprendimų skaičių.

Šakninė formulė: „x=arctg a + \pi n, n \in Z“.

4. Lygtis „ctg x=a“.

Taip pat turi begalinį bet kokių „a“ reikšmių sprendimų skaičių.

Šakninė formulė: „x=arcctg a + \pi n, n \in Z“.

Lentelėje pateiktų trigonometrinių lygčių šaknų formulės

Dėl sinuso:
Dėl kosinuso:
Tangentui ir kotangentui:
Formulės, skirtos spręsti lygtis, kuriose yra atvirkštinių trigonometrinių funkcijų:

Trigonometrinių lygčių sprendimo būdai

Bet kurios trigonometrinės lygties sprendimas susideda iš dviejų etapų:

paverčiant jį paprasčiausiu;
išspręskite paprasčiausią lygtį, gautą naudodamiesi aukščiau parašytomis šaknies formulėmis ir lentelėmis.

Pažvelkime į pagrindinius sprendimo būdus naudodami pavyzdžius.

Algebrinis metodas.

Šis metodas apima kintamojo pakeitimą ir jo pakeitimą lygybe.

Pavyzdys. Išspręskite lygtį: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 - x)+1=0`

`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0,

pakeiskite: „cos(x+\frac \pi 6)=y“, tada „2y^2-3y+1=0“,

randame šaknis: `y_1=1, y_2=1/2`, iš kurių seka du atvejai:

1. „cos(x+\frac \pi 6)=1“, „x+\frac \pi 6=2\pi n“, „x_1=-\frac \pi 6+2\pi n“.

2. `cos(x+\frac \pi 6)=1/2, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3- \frac \pi 6+2\pi n`.

Atsakymas: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.

Faktorizavimas.

Pavyzdys. Išspręskite lygtį: `sin x+cos x=1`.

Sprendimas. Perkelkime visus lygybės narius į kairę: `sin x+cos x-1=0`. Naudodami , mes transformuojame ir koeficientuojame kairę pusę:

„sin x – 2sin^2 x/2=0“,

„2sin x/2 cos x/2-2sin^2 x/2=0“,

„2sin x/2 (cos x/2-sin x/2) = 0“,

„sin x/2 =0“, „x/2 =\pi n“, „x_1=2\pi n“.
„cos x/2-sin x/2=0“, „tg x/2=1“, „x/2=arctg 1+ \pi n“, „x/2=\pi/4+ \pi n“ , „x_2=\pi/2+ 2\pi n“.

Atsakymas: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.

Redukcija į homogeninę lygtį

Pirmiausia turite sumažinti šią trigonometrinę lygtį į vieną iš dviejų formų:

„a sin x+b cos x=0“ ( vienalytė lygtis pirmas laipsnis) arba `a sin^2 x + b sin x cos x +c cos^2 x=0` (homogeninė antrojo laipsnio lygtis).

Tada padalykite abi dalis iš „cos x \ne 0“ – pirmuoju atveju ir iš „cos^2 x \ne 0“ – antruoju. Gauname „tg x“ lygtis: „a tg x+b=0“ ir „a tg^2 x + b tg x +c =0“, kurias reikia išspręsti žinomais metodais.

Pavyzdys. Išspręskite lygtį: `2 sin^2 x+sin x cos x - cos^2 x=1`.

Sprendimas. Užsirašykime dešinėje pusėje, pvz., „1=sin^2 x+cos^2 x“:

„2 sin^2 x+sin x cos x — cos^2 x=` „sin^2 x+cos^2 x“,

`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`

„sin^2 x+sin x cos x — 2 cos^2 x=0“.

Tai yra vienalytė antrojo laipsnio trigonometrinė lygtis, jos kairę ir dešinę puses padaliname iš `cos^2 x \ne 0`, gauname:

`\frac (sin^2 x)(cos^2 x)+\frac(sin x cos x)(cos^2 x) — \frac(2 cos^2 x)(cos^2 x)=0

„tg^2 x+tg x – 2=0“. Įveskime pakaitalą „tg x=t“, todėl gauname „t^2 + t - 2=0“. Šios lygties šaknys yra „t_1=-2“ ir „t_2=1“. Tada:

„tg x=-2“, „x_1=arctg (-2)+\pi n“, „n \in Z“
„tg x=1“, „x=arctg 1+\pi n“, „x_2=\pi/4+\pi n“, „n \in Z“.

Atsakymas. „x_1=arctg (-2)+\pi n“, „n \in Z“, „x_2=\pi/4+\pi n“, „n \in Z“.

Perėjimas prie pusės kampo

Pavyzdys. Išspręskite lygtį: "11 sin x - 2 cos x = 10".

Sprendimas. Taikykime formules dvigubas kampas, gaunasi: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x/2+10 cos^ 2 x/2''

„4 tg^2 x/2 – 11 tg x/2 +6=0“.

Taikant aukščiau pateiktą algebrinis metodas, gauname:

„tg x/2=2“, „x_1=2 arctg 2+2\pi n“, „n \in Z“,
„tg x/2=3/4“, „x_2=arctg 3/4+2\pi n“, „n \in Z“.

Atsakymas. „x_1=2 arctg 2+2\pi n, n \in Z“, „x_2=arctg 3/4+2\pi n“, „n \in Z“.

Pagalbinio kampo įvedimas

Trigonometrinėje lygtyje „a sin x + b cos x =c“, kur a,b,c yra koeficientai, o x yra kintamasis, padalykite abi puses iš „sqrt (a^2+b^2)“:

`\frac a(sqrt (a^2+b^2)) sin x +` `\frac b(sqrt (a^2+b^2)) cos x =` `\frac c(sqrt (a^2) ) +b^2))".

Kairėje pusėje esantys koeficientai turi sinuso ir kosinuso savybes, būtent jų kvadratų suma lygi 1, o moduliai ne didesni kaip 1. Pažymime juos taip: `\frac a(sqrt (a^2) +b^2))=cos \varphi` , ` \frac b(sqrt (a^2+b^2)) =sin \varphi`, `\frac c(sqrt (a^2+b^2)) =C`, tada:

`cos \varphi sin x + sin \varphi cos x =C`.

Pažvelkime atidžiau į šį pavyzdį:

Pavyzdys. Išspręskite lygtį: `3 sin x+4 cos x=2`.

Sprendimas. Padalinkite abi lygybės puses iš `sqrt (3^2+4^2)', gausime:

`\frac (3 sin x) (sqrt (3^2+4^2))+` `\frac(4 cos x)(sqrt (3^2+4^2))=` `\frac 2(sqrt (3^2+4^2))".

„3/5 sin x+4/5 cos x=2/5“.

Pažymime `3/5 = cos \varphi` , `4/5=sin \varphi`. Kadangi „sin \varphi>0“, „cos \varphi>0“, tada kaip pagalbinis kampas imkime `\varphi=arcsin 4/5`. Tada rašome savo lygybę tokia forma:

„cos \varphi sin x+sin \varphi cos x=2/5“.

Taikydami sinuso kampų sumos formulę, rašome savo lygybę tokia forma:

„sin (x+\varphi)=2/5“,

„x+\varphi=(-1)^n arcsin 2/5+ \pi n“, „n \in Z“,

`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z.

Atsakymas. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z.

Trupmeninės racionalios trigonometrinės lygtys

Tai lygybės su trupmenomis, kurių skaitikliuose ir vardikliuose yra trigonometrinių funkcijų.

Pavyzdys. Išspręskite lygtį. „\frac (sin x)(1+cos x)=1-cos x“.

Sprendimas. Padauginkite ir padalinkite dešinę lygybės pusę iš „(1+cos x)“. Rezultate gauname:

`\frac (sin x)(1+cos x)=` `\frac ((1-cos x)(1+cos x))(1+cos x)

`\frac (sin x)(1+cos x)=` `\frac (1-cos^2 x)(1+cos x)`

`\frac (sin x)(1+cos x)=` `\frac (sin^2 x)(1+cos x)`

`\frac (sin x)(1+cos x)-` `\frac (sin^2 x)(1+cos x)=0

„\frac (sin x-sin^2 x)(1+cos x)=0“.

Atsižvelgiant į tai, kad vardiklis negali būti lygus nuliui, gauname `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z.

Prilyginkime trupmenos skaitiklį nuliui: „sin x-sin^2 x=0“, „sin x(1-sin x)=0“. Tada „sin x=0“ arba „1-sin x=0“.

„sin x=0“, „x=\pi n“, „n \in Z“.
„1-sin x=0“, „sin x=-1“, „x=\pi /2+2\pi n, n \in Z“.

Atsižvelgiant į tai, kad ` x \ne \pi+2\pi n, n \in Z, sprendiniai yra `x=2\pi n, n \in Z` ir `x=\pi /2+2\pi n` , „n \in Z“.

Atsakymas. „x=2\pi n“, „n \in Z“, „x=\pi /2+2\pi n“, „n \in Z“.

Trigonometrija, o ypač trigonometrinės lygtys, naudojamos beveik visose geometrijos, fizikos ir inžinerijos srityse. Mokymasis prasideda 10 klasėje, vieningam valstybiniam egzaminui visada yra užduočių, todėl pasistenkite atsiminti visas trigonometrinių lygčių formules – jos jums tikrai pravers!

Tačiau net nereikia jų įsiminti, svarbiausia suprasti esmę ir mokėti ją išvesti. Tai nėra taip sunku, kaip atrodo. Įsitikinkite patys žiūrėdami vaizdo įrašą.

Paprastų trigonometrinių lygčių sprendimas.

Sprendžiant bet kokio sudėtingumo trigonometrines lygtis galiausiai reikia išspręsti paprasčiausias trigonometrines lygtis. Ir šiame geriausias pagalbininkas vėl pasirodo, kad tai trigonometrinis apskritimas.

Prisiminkime kosinuso ir sinuso apibrėžimus.

Kampo kosinusas yra taško abscisė (ty koordinatė išilgai ašies). vieneto ratas, atitinkantis sukimąsi tam tikru kampu.

Kampo sinusas yra vienetinio apskritimo taško, atitinkančio sukimąsi tam tikru kampu, ordinatė (ty koordinatė išilgai ašies).

Teigiama judėjimo kryptis išilgai trigonometrinis ratas Atsižvelgiama į judėjimą prieš laikrodžio rodyklę. 0 laipsnių (arba 0 radianų) pasukimas atitinka tašką su koordinatėmis (1; 0)

Šiuos apibrėžimus naudojame paprastoms trigonometrinėms lygtims išspręsti.

1. Išspręskite lygtį

Šią lygtį tenkina visos sukimosi kampo reikšmės, atitinkančios apskritimo taškus, kurių ordinatė yra lygi .

Ordinačių ašyje pažymėkime tašką su ordinatėmis:

Vykdykime horizontali linija lygiagrečiai x ašiai, kol susikerta su apskritimu. Gauname du taškus, gulinčius ant apskritimo ir turinčius ordinatę. Šie taškai atitinka sukimosi kampus radianais:

Jei mes, palikdami tašką, atitinkantį sukimosi kampą radianais, apeisime pilnas ratas, tada pateksime į tašką, atitinkantį sukimosi kampą radianui ir turintį tą pačią ordinatę. Tai yra, šis sukimosi kampas taip pat atitinka mūsų lygtį. Galime padaryti tiek „tuščiosios eigos“ apsisukimų, kiek norime, grįždami į tą patį tašką, ir visos šios kampų reikšmės patenkins mūsų lygtį. „Tuščiosios eigos“ apsisukimų skaičius bus pažymėtas raide (arba). Kadangi mes galime padaryti šias revoliucijas tiek teigiamai, tiek neigiamai neigiama kryptis, (arba ) gali turėti bet kokią sveikojo skaičiaus reikšmę.

Tai yra, pirmoji pradinės lygties sprendinių serija turi tokią formą:

, , - sveikųjų skaičių rinkinys (1)

Panašiai antroji sprendimų serija turi tokią formą:

, Kur,. (2)

Kaip jau galėjote atspėti, ši sprendimų serija pagrįsta tašku apskritime, atitinkančiu sukimosi kampą .

Šios dvi sprendimų serijos gali būti sujungtos į vieną įrašą:

Jei imsime (tai yra, net) šiame įraše, gausime pirmąją sprendimų seriją.

Jei imsime (ty nelyginį) šiame įraše, gausime antrą sprendinių seriją.

2. Dabar išspręskime lygtį

Kadangi tai yra vienetinio apskritimo taško abscisė, gauta pasukus kampu, tašką pažymime abscise ašyje:

Vykdykime vertikali linija lygiagrečiai ašiai, kol susikerta su apskritimu. Gausime du taškus, gulėdami ant apskritimo ir turėdami abscisę. Šie taškai atitinka sukimosi kampus ir radianais. Prisiminkite, kad judėdami pagal laikrodžio rodyklę gauname neigiamas kampas sukimasis:

Užrašykime dvi sprendimų serijas:

(Į norimą tašką patenkame eidami iš pagrindinio pilno rato, tai yra.

Sujungkime šias dvi serijas į vieną įrašą:

3. Išspręskite lygtį

Liestinė eina per tašką, kurio koordinatės (1,0) yra lygiagrečios OY ašiai

Pažymėkime jame tašką, kurio ordinatė lygi 1 (ieškome kampų liestinės, lygios 1):

Sujungkime šį tašką prie koordinačių pradžios tiesia linija ir pažymėkime tiesės susikirtimo taškus su vienetiniu apskritimu. Tiesios linijos ir apskritimo susikirtimo taškai atitinka sukimosi kampus ir :

Kadangi taškai, atitinkantys mūsų lygtį atitinkančius sukimosi kampus, yra vienas nuo kito radianų atstumu, sprendimą galime parašyti taip:

4. Išspręskite lygtį

Kotangentų linija eina per tašką, kurio vieneto apskritimo koordinatės yra lygiagrečios ašiai.

Kotangentų eilutėje pažymėkime tašką abscise -1:

Sujungkime šį tašką su tiesės pradžios tašku ir tęskime tol, kol susikirs su apskritimu. Ši tiesi linija kirs apskritimą taškuose, kurie atitinka sukimosi kampus į ir radianais:

Kadangi šie taškai yra atskirti vienas nuo kito atstumu, lygiu , Tada bendras sprendimasŠią lygtį galime parašyti taip:

Pateiktuose pavyzdžiuose, iliustruojančiuose paprasčiausių trigonometrinių lygčių sprendimą, buvo panaudotos trigonometrinių funkcijų lentelės reikšmės.

Tačiau jei dešinėje lygties pusėje nėra lentelės vertė, tada reikšmę pakeičiame bendruoju lygties sprendiniu:

SPECIALIEJI SPRENDIMAI:

Pažymėkime apskritimo, kurio ordinatė lygi 0, taškus:

Pažymėkime vieną tašką apskritime, kurio ordinatė yra 1:

Pažymėkime vieną tašką apskritime, kurio ordinatė lygi -1:

Kadangi įprasta nurodyti reikšmes, artimiausias nuliui, sprendimą rašome taip:

Pažymėkime apskritimo, kurio abscisė lygi 0, taškus:

5.
Pažymėkime vieną tašką apskritime, kurio abscisė lygi 1:

Pažymime vieną tašką apskritime, kurio abscisė lygi -1:

Ir šiek tiek sudėtingesni pavyzdžiai:

Sinusas lygus vienam, jei argumentas lygus

Mūsų sinuso argumentas yra lygus, todėl gauname:

Abi lygybės puses padalinkite iš 3:

Atsakymas:

Kosinusas yra nulis, jei kosinuso argumentas yra

Mūsų kosinuso argumentas yra lygus , todėl gauname:

Išreikškime , norėdami tai padaryti, pirmiausia judame į dešinę su priešingu ženklu:

Supaprastinkime dešinę pusę:

Padalinkite abi puses iš -2:

Atkreipkite dėmesį, kad ženklas prieš terminą nesikeičia, nes k gali turėti bet kokią sveikojo skaičiaus reikšmę.

Atsakymas:

Ir galiausiai žiūrėkite vaizdo pamoką „Šaknų pasirinkimas trigonometrinėje lygtyje naudojant trigonometrinis ratas"

Tai baigia mūsų pokalbį apie paprastų trigonometrinių lygčių sprendimą. Kitą kartą pakalbėsime, kaip apsispręsti.

Trigonometrinės lygtys. Pirmoje matematikos egzamino dalyje yra užduotis, susijusi su lygties sprendimu - tai paprastos lygtys kurios išsprendžiamos per kelias minutes, daugelį tipų galima išspręsti žodžiu. Apima: tiesines, kvadratines, racionaliąsias, neracionaliąsias, eksponentines, logaritmines ir trigonometrines lygtis.

Šiame straipsnyje apžvelgsime trigonometrines lygtis. Jų sprendimas tiek skaičiavimų apimtimi, tiek sudėtingumu skiriasi nuo kitų šioje dalyje pateiktų problemų. Neišsigąskite, žodis „sunkumas“ reiškia santykinį jų sunkumą, palyginti su kitomis užduotimis.

Be pačių lygties šaknų, būtina nustatyti didžiausią neigiamą arba mažiausią teigiama šaknis. Tikimybė, kad egzamino metu gausite trigonometrinę lygtį, žinoma, yra maža.

Šioje Vieningo valstybinio egzamino dalyje jų yra mažiau nei 7 proc. Tačiau tai nereiškia, kad juos reikia ignoruoti. C dalyje taip pat reikia išspręsti trigonometrinę lygtį, todėl gerai suprasti sprendimo techniką ir suprasti teoriją tiesiog būtina.

Matematikos trigonometrijos skyriaus supratimas labai nulems jūsų sėkmę sprendžiant daugelį problemų. Primenu, kad atsakymas yra sveikasis arba baigtinis skaičius dešimtainis. Kai gausite lygties šaknis, BŪTINAI patikrinkite. Tai neužims daug laiko ir išgelbės jus nuo klaidų.

Ateityje taip pat pažvelgsime į kitas lygtis, nepraleiskite! Prisiminkime trigonometrinių lygčių šaknų formules, jas turite žinoti:

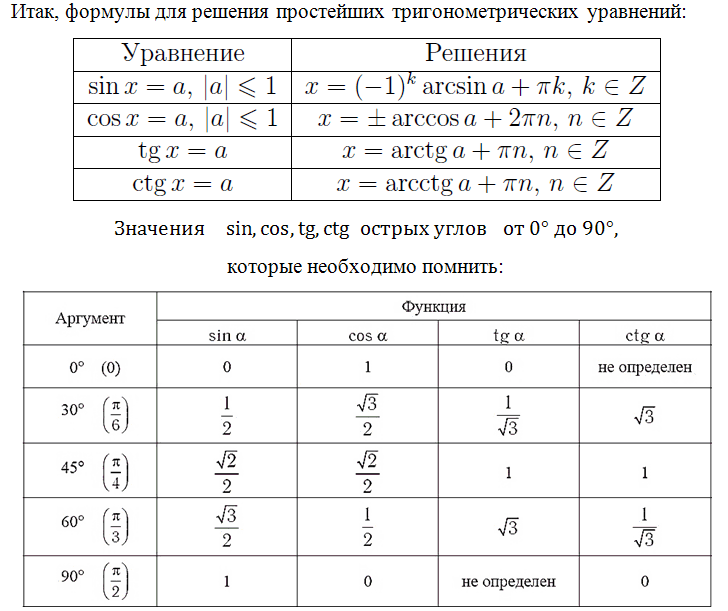
Žinios apie šias vertybes yra būtinos, tai yra „abėcėlė“, be kurios neįmanoma susidoroti su daugeliu užduočių. Puiku, jei jūsų atmintis gera, jūs lengvai išmokote ir įsiminėte šias vertybes. Ką daryti, jei to padaryti negalite, jūsų galvoje yra sumaištis, bet jūs tiesiog sutrikote laikydami egzaminą. Būtų gaila prarasti tašką, nes skaičiavimuose įrašėte neteisingą vertę.

Šios reikšmės yra paprastos, jos taip pat pateiktos teorijoje, kurią gavote antrajame laiške užsiprenumeravę naujienlaiškį. Jei dar neužsiprenumeravote, padarykite tai! Ateityje taip pat apžvelgsime, kaip šias vertes galima nustatyti iš trigonometrinio apskritimo. Ne veltui ji vadinama „auksine trigonometrijos širdimi“.

Leiskite man iš karto paaiškinti, kad būtų išvengta painiavos, kad toliau nagrinėjamose lygtyse pateikiami arcsinuso, arkosino ir arktangento apibrėžimai naudojant kampą. X atitinkamoms lygtims: cosx=a, sinx=a, tgx=a, kur X taip pat gali būti išraiška. Toliau pateiktuose pavyzdžiuose mūsų argumentas tiksliai nurodytas išraiška.

Taigi, apsvarstykime šias užduotis:

Raskite lygties šaknį:

Savo atsakyme užrašykite didžiausią neigiamą šaknį.

Cos x = a lygties sprendimas yra dvi šaknys:

Apibrėžimas: Tegul skaičius a modulyje neviršija vieneto. Skaičiaus lankinis kosinusas yra kampas x, esantis intervale nuo 0 iki Pi, kurio kosinusas lygus a.

Reiškia

Išreikškime x:

Raskime didžiausią neigiamą šaknį. Kaip tai padaryti? Pakeiskime skirtingos reikšmės n į gautas šaknis, apskaičiuokite ir pasirinkite didžiausią neigiamą.

Skaičiuojame:

Kai n = – 2 x 1 = 3 (– 2) – 4,5 = – 10,5 x 2 = 3 (– 2) – 5,5 = – 11,5

Kai n = – 1 x 1 = 3 (– 1) – 4,5 = – 7,5 x 2 = 3 (– 1) – 5,5 = – 8,5

Kai n = 0 x 1 = 3,0 – 4,5 = – 4,5 x 2 = 3,0 – 5,5 = – 5,5

Kai n = 1 x 1 = 3,1 – 4,5 = – 1,5 x 2 = 3,1 – 5,5 = – 2,5

Kai n = 2 x 1 = 3,2 – 4,5 = 1,5 x 2 = 3,2 – 5,5 = 0,5

Mes nustatėme, kad didžiausia neigiama šaknis yra –1,5

Atsakymas: –1,5

Spręskite patys:

Išspręskite lygtį:

Lygties sin x = a sprendimas yra dvi šaknys:

Bet kuris (jis sujungia abu pirmiau nurodytus dalykus):

Apibrėžimas: Tegul skaičius a modulyje neviršija vieneto. Skaičiaus arcsinusas yra kampas x, esantis intervale nuo –90° iki 90°, kurio sinusas lygus a.