Tekstinė leidinio dalis
Turinys
Įvadas……………………………………………………………………..3 I skyrius. Iš kompleksinių skaičių istorijos……………………………… ………………………… ............4 II skyrius. Kompleksinių skaičių metodo pagrindai………………………………………6 III skyrius. Trikampio geometrija kompleksiniais skaičiais……………………......12 IV skyrius. Sprendimas Vieningo valstybinio egzamino problemos ir įvairios olimpiados naudojant kompleksinių skaičių metodą…………………………………………………………………………………………………………………………………………………………… ……… ……………………………………….24 Bibliografija…………………………………………………………………..25
Įvadas
Plačiai žinoma sudėtingų skaičių svarba matematikoje ir jos pritaikymuose. Kompleksinių skaičių algebra sėkmingai gali būti naudojama elementariojoje geometrijoje, trigonometrijoje, judesių ir panašumų teorijoje, taip pat elektrotechnikoje, įvairiose mechaninėse ir fizinių problemų. Planimetrijoje kompleksinių skaičių metodas leidžia spręsti problemas tiesiogiai apskaičiuojant naudojant paruoštas formules. Tai yra šio metodo paprastumas, palyginti su vektoriumi ir koordinuoti metodus, geometrinių transformacijų metodu, reikalaujančiu iš mokinių didelio intelekto ir ilgų paieškų. Jau kelis tūkstantmečius trikampis buvo geometrijos simbolis. Galima net sakyti, kad trikampis yra geometrijos atomas. Bet kurį daugiakampį galima suskirstyti į trikampius, o jo savybių tyrimas priklauso nuo jo komponentų trikampių savybių. Pažiūrėkime, kaip veikia kompleksinių skaičių metodas įrodant trikampio savybes iš mokyklos kursas planimetrija, taip pat vieningo valstybinio egzamino C-4 uždaviniams spręsti. 2
I skyrius. Iš kompleksinių skaičių istorijos,
Pirmą kartą, regis, menami kiekiai paminėti garsiajame veikale „Didysis menas, arba Apie algebrinės taisyklės» Cardano (1545), viduje oficialus sprendimas dviejų skaičių, kurių suma yra 10, apskaičiavimo uždavinys, o padauginus gauname 40. Šiam uždaviniui jis gavo kvadratinę vieno iš narių lygtį ir rado jos šaknis: 5 + √ − 15 ir 5 − √ − 15. Komentuodamas sprendimą, jis rašė: „šie sudėtingiausi dydžiai yra nenaudingi, nors ir labai išradingi“ ir „Aritmetiniai svarstymai tampa vis sunkiau suvokiami ir pasiekia ribą, kuri yra tokia pat subtili, kaip ir nenaudinga“. Galimybę panaudoti įsivaizduojamus dydžius sprendžiant kubinę lygtį, vadinamuoju neredukuojamuoju atveju (kai tikrosios daugianario šaknys išreiškiamos per įsivaizduojamų dydžių kubines šaknis), pirmą kartą aprašė Bombelli (1572). Jis pirmasis aprašė kompleksinių skaičių sudėties, atimties, daugybos ir dalybos taisykles, tačiau vis tiek laikė jas nenaudingu ir gudriu „išradimu“. Išraiškos, vaizduojamos forma a + b √ − 1, atsirandančios sprendžiant kvadratines ir kubines lygtis, pradėtas vadinti „įsivaizduojamais“. XVI-XVII a Dekarto, kuris juos taip pavadino, atmetus jų tikrovę ir daugeliui kitų žymių XVII amžiaus mokslininkų, iniciatyva įsivaizduojamų dydžių prigimtis ir teisė į egzistavimą atrodė labai abejotini, kaip ir tuo metu jie buvo laikomi abejotini. neracionalūs skaičiai, ir net neigiamos reikšmės. Nepaisant to, matematikai drąsiai taikė formalūs metodai realiųjų dydžių ir kompleksinių algebrų, net iš tarpinių kompleksinių gaudavo teisingus realius rezultatus, ir tai negalėjo kelti pasitikėjimo. Ilgą laiką buvo neaišku, ar visos operacijos su kompleksiniais skaičiais veda prie sudėtingų ar realių rezultatų, ar, pavyzdžiui, ištraukus šaknį, galima atrasti kitokį naują skaičių tipą. n laipsnio šaknų išreiškimo problema duotas numeris buvo išspręsta Moivre (1707) ir Cotes (1722) darbuose. Simbolį įsivaizduojamam vienetui žymėti pasiūlė Euleris (1777 m., paskelbtas 1794 m.), kuris tam paėmė pirmą lotyniško žodžio raidę. imaginarius – įsivaizduojamas. Jis išplatino viską standartinės funkcijos , įskaitant logaritmą, į sudėtingą sritį. Euleris taip pat išreiškė mintį 1751 m., kad kompleksinių skaičių laukas algebriškai uždaras. D'Alembertas (1747) padarė tą pačią išvadą, bet pirmas griežtas įrodymas Šis faktas priklauso Gaussui (1799). Gaussas terminą „sudėtinis skaičius“ plačiai pradėjo vartoti 1831 m., nors anksčiau šis terminas buvo vartojamas ta pačia prasme. prancūzų matematikas
Kompleksinių skaičių, kaip realiųjų skaičių porų, aritmetinį (standartinį) modelį sukonstravo Hamiltonas (1837); tai įrodė jų savybių nuoseklumą. Daug anksčiau, 1685 m., savo darbe „Algebra“, Wallis (Anglija) parodė, kad sudėtingos šaknys Kvadratinę lygtį su realiais koeficientais galima pavaizduoti geometriškai, plokštumos taškais. Bet tai liko nepastebėta. Kitą kartą sudėtingų skaičių ir operacijų su jais geometrinė interpretacija pasirodė Wesselio darbe (1799). Šiuolaikinis geometrinis vaizdas, kartais vadinamas „Argando diagrama“, pradėtas naudoti po J. R. Argando darbo paskelbimo 1806 ir 1814 m., kuris nepriklausomai pakartojo Wesselio išvadas. Terminus „modulis“, „argumentas“ ir „konjuguotas skaičius“ įvedė Koši. Taip buvo nustatyta, kad kompleksiniai skaičiai Jie taip pat tinka atlikti grynai algebrines vektorių sudėjimo, atimties, daugybos ir dalybos operacijas plokštumoje, kurios labai pakeitė vektorinę algebrą. 4
II skyrius. Kompleksinio skaičiaus metodo pagrindai
[
1
]
,
[2], [3] [4] Geometrinis kompleksinių skaičių aiškinimas Atkarpos ilgis Duotas stačiakampis Dekarto sistema koordinates plokštumoje, kompleksinis skaičius z = x+iy (i 2 = -1) gali būti vienas su vienu susietas su plokštumos tašku M su koordinatėmis x, y (1 pav.): z = x + iy ↔M (x, y ) ↔M (z) . Tada skaičius z vadinamas kompleksine taško M koordinate. Kadangi Euklido plokštumos taškų aibė vienas su vienu atitinka kompleksinių skaičių aibę, ši plokštuma dar vadinama kompleksinių skaičių plokštuma. Dekarto koordinačių sistemos pradžia O vadinama kompleksinių skaičių plokštumos pradiniu arba nuliniu tašku. Kai = 0, skaičius z yra tikras. Tikrieji skaičiai yra pavaizduoti taškais x ašyje, todėl jis vadinamas tikroji ašis. Kai x=0, skaičius z yra tik įsivaizduojamas: z=iy. Įsivaizduojami skaičiai vaizduojami taškais y ašyje, todėl ji vadinama įsivaizduojama ašimi. Nulis yra tikrasis ir tik įsivaizduojamas skaičius. Atstumas nuo O plokštumos pradžios iki taško M(z) vadinamas kompleksinio skaičiaus z moduliu ir žymimas |z| arba r: | z | = r = | OM | = √ x 2 + y 2 Jei φ yra orientuotas kampas, sudarytas vektoriaus ⃗ OM su x ašimi, tai pagal sinuso ir kosinuso funkcijos apibrėžimą sin φ = y r, cos φ = x r 5
iš kur x = r cos φ, y = r sin φ, taigi z = r (cos φ + sin φ). Šis kompleksinio skaičiaus z vaizdavimas vadinamas jo
trigonometrija
cheskoe
forma.
algebrinė
šio numerio forma. Trigonometriniame vaizdavime kampas vadinamas kompleksinio skaičiaus argumentu ir taip pat žymimas arg z: φ = arg z Jeigu duotas kompleksinis skaičius z = x + iy, vadinasi skaičius ´ z = x − iy
kompleksinis konjugatas
(arba tiesiog
konjugatas
) iki šio skaičiaus z. Tada akivaizdu, kad skaičius z taip pat yra konjuguotas su skaičiumi ´z. Taškai M(z) ir M 1 (´ z) yra simetriški x ašies atžvilgiu. Iš lygybės z = ´ z išplaukia, kad y = 0 ir atvirkščiai. Tai reiškia, kad
skaičius lygus
su jo konjugatu yra tikras ir atvirkščiai.
Taškai su sudėtingomis koordinatėmis z ir -z yra simetriški pradinio taško O atžvilgiu. Taškai su kompleksinėmis koordinatėmis z ir −´ z yra simetriški y ašies atžvilgiu. Iš lygybės z = ´ z išeina, kad x = 0 ir atvirkščiai. Todėl sąlyga z =− ´ z yra grynai įsivaizduojamo skaičiaus kriterijus. Bet kuriam skaičiui z akivaizdžiai | z | = | ´z | =¿− z ∨¿∨−´ z ∨¿ .
Suma ir produktas
du konjuguoti kompleksiniai skaičiai yra realieji skaičiai: z + ´ z = 2 z, z ´ z = x 2 + y 2 =¿ z 2 ∨¿. Skaičius, susietas su komplekso 6 suma, sandauga arba koeficientu
skaičiai yra atitinkamai skaičių suma, sandauga arba koeficientas, susietas su duotais kompleksiniais skaičiais: ´ z 1 + z 2 = ´ z 1 + ´ z 2 ; ´z 1 z 2 = ´z 1´ z 2; ´ z 1: z 2 = ´ z 1: ´ z 2 Šias lygybes galima lengvai patikrinti naudojant operacijų su kompleksiniais skaičiais formules. Jei a ir b - sudėtingos koordinatės atitinkamai taškais A ir B, tada skaičius c = a + b yra taško C koordinatė, kad ⃗ OC = ⃗ OA + ⃗ OB (3 pav.). Kompleksinis skaičius d = a − b atitinka tokį tašką D, kad ⃗ OD = ⃗ OA − ⃗ OB . Atstumas tarp taškų A ir B yra | ⃗BA | = | ⃗ OD | =¿ a − b ∨¿: ¿ AB ∨¿∨ a − b ∨¿ (1) Kadangi ¿ z ∨ 2 = z ´ z , tai ¿ AB ∨ 2 =(a − b) (´ a − ´ b) . (2)
Lygtis
z´z = r 2
apibrėžia apskritimą su centru
Apie spindulį
r.
Ryšys AC CB = λ, (λ ≠ − 1), kuriame taškas C dalijasi šis segmentas AB, išreiškiamas kompleksinėmis šių taškų koordinatėmis taip: λ = c − a b − c, λ = ´ λ, iš kur c = a + λb 1 + λ (3) Jei λ = 1, taškas C yra vidurio taškas segmento AB, ir atvirkščiai. Tada: c = 1 2 (a + b) (4) Kompleksinių skaičių daugyba Kompleksinių skaičių daugyba atliekama pagal formulę, Tai yra, | a b | = | a || b | ir 7
Lygiagretumas ir statmenumas Trijų taškų kolineariškumas Tegul kompleksinių skaičių plokštumoje pateikiami taškai A(a) ir B(b). Vektoriai ⃗ OA ir ⃗ OB nukreipiami kartu tada ir tik tada, kai arg a = arg b, t. y. kai arg a – arg b=arg a b =0 (dalinant kompleksinius skaičius, daliklio argumentas atimamas iš dividendai).
Taip pat akivaizdu, kad šie vektoriai yra nukreipti priešingomis kryptimis tada ir tik tada, kai arg a - arg b= arg a b = ± π. Sudėtiniai skaičiai su argumentais 0, π, - π yra tikri.
O, A, B taškų kolineariškumo kriterijus: Kad taškai A(a) ir B(b) būtų lygiagrečiai su pradiniu tašku O, būtina ir pakanka, kad koeficientas a b būtų tikrasis skaičius, ty a b = ´ a ´ b arba a ´ b = ´ a b (6 ) Dabar paimkite taškus A(a), B(b), C(c), D(d). Vektoriai ⃗ BA ir ⃗ DC kolis yra neariniai tada ir tik tada, kai taškai apibrėžti kompleksu skaičiai a-b
ir с-d yra kolineariniai su pradžia O. Pastaba: 1. Remdamiesi (6) turime: ⃗ AB ∨¿ ⃗ CD↔ (a − b) (´ c − ´ d) =(´ a − ´ b ) (c – d) ; (8) 2. Jei taškai A, B, C, D priklauso vienetiniam apskritimui z ´ z = 1, tai ´ a = 1 a; ´b = 1b; ´c = 1c; ´ d = 1 d, todėl sąlyga (8) įgauna tokią formą: ⃗ AB ∨¿ ⃗ CD↔ ab = cd ; (9) 3. Taškų A, B, C kolineariškumas apibūdinamas vektorių ⃗AB ir ⃗AC kolineariškumu. Naudodami (8) gauname: (a − b) (´ a −´ c) =(´ a − ´ b) (a − c) (10) Tai yra taškų A, B, C priklausymo kriterijus. į tą pačią tiesią liniją. Jis gali būti pavaizduotas simetriška forma a (´ b −´ c) + b (´ c −´ a) + c (´ a − ´ b) = 0 (11) 8 Jei taškai A ir B priklauso vienetiniam apskritimui z ´ z = 1, tai ´ a = 1 a; ´ b = 1 b, todėl kiekvienas ryšys (10) ir (11) paverčiamas (sumažinus (a-b)) į šiuos: c + ab ´ c = a + b (12) Taškai A ir B yra fiksuoti, o tašką C laikysime kintamuoju, perskirdami jo koordinatę z. Tada kiekvienas gautas ryšys (10), (11), (12) bus tiesės AB lygtis: (´ a − ´ b) z + (b − a) ´ z + a ´ b − b ´ a = 0, (10a) z + ab ´ z = a + b (12a) Konkrečiai, tiesioginis OA turi lygtį a ´ z = ´ a z yra grynai įsivaizduojami, todėl OA ⊥ OB↔ a b = − ´ a ´ b arba OA ⊥ OB↔a ´ b + ´ a b = 0 (13) Atkarpų AB ir CD statmenumą lemia lygybė (a). − b) (´ c − ´ d) + (´ a − ´ b) (c − d) = 0 (14) Visų pirma, kai taškai A, B, C, D priklauso vienetiniam apskritimui z ´ z = 1 , tada priklausomybė (14) supaprastinama: ab + cd = 0 (15) Išreiškiama vektorių skaliarinė sandauga. vektoriai ⃗ OA ir ⃗ OB per taškų A ir B kompleksines koordinates a ir b. Tegu a=x 1 +iy 1 , b=x 2 +iy 2 . Tada a b + a b=(x 1 +iy 1)(x 2 -iy 2)+(x 1 -iy 1)(x 2 +iy 2)=2(x 1 x 2 +y 1 y 2) = 2 ⃗ OA∙⃗OB. Taigi, ⃗ OA ∙ ⃗ OB = 1 2 (a b + ab) (16) 9
Dabar duokime keturis savavališki taškai A(a), B(b), C(c), D(d) pagal jų kompleksines koordinates. Tada 2 ⃗ AB ∙ ⃗ CB = 1 2 (a-b)(c - d)+(a - b)(c-d) (17) Kampai Sutikime simboliu ∠ (AB ,CD) pažymėti teigiamai orientuotą kampą per kurį vektorių ⃗ reikia pasukti AB taip, kad jis susilygintų su vektoriumi ⃗ CD. Tada cos ∠ (AB, CD)= (d − c) (´ b − ´ a) +(´ d −´ c)(b − a) 2 | d − c || b − a |
(18) sin ∠ (AB ,CD)= (d − c) (´ b −´ a) +(´ d −´ c)(b − a) 2 i | d − c || b − a |
(19) Sekantų susikirtimo taškas su apskritimu Jei taškai A, B, C ir D yra apskritime z ´ z = 1, tai susikirtimo taško kompleksinė koordinatė randama pagal formulę ´ z = (a + b) − (c + d) ab − cd (20) Jei AB yra statmena CD, tai z= 1 2 (a+b+c+d) (21) Apskritimo liestinių susikirtimo taškas 10
Apskritimo z ´ z =1 liestinių susikirtimo taško kompleksinė koordinatė jo taškuose A(a) ir B(b) randama pagal formulę z= 2ab a + b (22) Stačiakampė taško projekcija į tiesę Stačiakampė taško M(m) projekcija į tiesę AB, kur A(a) ir B(b) randama pagal formulę Tuo atveju, kai A ir B priklauso vienetiniam apskritimui z= 1 2 (a + b + m − cb m) .
III skyrius.
Iš kur kyla h=a+b+c. (24) Gauta išraiška apima trikampio viršūnių koordinates simetriškai, todėl trečioji trikampio aukštinė eina per pirmųjų dviejų panašių trikampių susikirtimo tašką [2,1] Trikampiai ABC ir A 1 B 1 C 1 yra panašūs ir vienodai orientuoti (pirmosios rūšies panašumas), jei B 1 =kAB, A 1 B 1 =kAC ir kampai B 1 A 1 C 1 ir BAC yra lygūs (kampai orientuoti). Naudojant kompleksinius skaičius, šias lygybes galima užrašyti taip: |a 1 −b 1 |=k|a−b|, |a 1 −c 1 |=k|a−c|,arg c 1 − a 1 b 1 − a 1 =arg c − a b − a . Dvi lygybės yra lygiavertės vienai su 1 − a 1 c − a = b 1 − a 1 b − a = σ , (25), kur σ yra kompleksinis skaičius, |σ|=k-panašumo koeficientas. Jei σ tikrasis, tai c 1 − a 1 c − a = ´ c 1 − ´ a 1 ´ c − ´ a , kur AC║A 1 C 1. Vadinasi, trikampiai ABC ir A 1 B 1 C 1 yra homotetiniai. Santykis (25) yra būtinas ir pakankama būklė kad trikampiai ABC ir A 1 B 1 C 1 būtų panašūs ir vienodai orientuoti. Jai gali būti suteikta simetriška forma ab 1 +bc 1 +ca 1 =ba 1 +cb 1 +ac 1 (25a) Lygūs trikampiai Jei | σ | = 1, tada trikampiai ABC ir A 1 B 1 C 1 yra lygūs. Tada santykis (25) yra vienodai orientuotų trikampių lygybės ženklas, o santykis (26) yra priešingos krypties trikampių lygybės ženklas. Reguliarūs trikampiai Jei reikia, kad būtų orientuotas trikampis ABC buvo panašus į orientuotą trikampį BCA, tada trikampis ABC bus taisyklingas. 12
Todėl iš (25) gauname būtiną ir pakankamą sąlygą, kad trikampis ABC būtų taisyklingas (a−b) 2 +(b−c) 2 +(c−a) 2 =0 (27) Trikampio plotas (įrodė autorius) Išvedame teigiamai orientuoto trikampio ABC ploto S formulę: S = 1 2 | AB || AC | sin ∠ (AB , AC)= 1 4i ((c − a) (´ b − ´ a) − (b − a) (´ c −´ a)) = − 1 4i (a (´ b −´ c) + b (´ c − ´ a) + c (´ a − ´ b)) arba S = i 4 (a (´ b − ´ c) + b (´ c − ´ a) + c (´ a − ´ b) )) (28) Jei trikampis ABCįrašytas į apskritimą z ´ z = 1, tada formulė (28) paverčiama tokia forma: S = i 4 (a − b)(b − c)(c − a) abc (29) Teorema apie a vidurinę liniją trikampis (įrodė autorius)
Teorema
. Vidurinė linija trikampis yra lygiagretus pagrindui ir lygus jo pusei. Įrodymas. Tegul taškai M ir N yra kraštinių AB ir BC vidurio taškai, tada m = b 2 ; n = b + c 2 . Kadangi z 2 =z ´ z, tai MN 2 =(m-n)(´ m - ´ n)=(b 2 - b + c 2)(´ b 2 – ´ b + ´ c 2)= b ´ b 4 − b ´ b + b ´ c 4 − b ´ b + ´ b c 4 + b ´ b + b ´ c + ´ b c + c ´ c 4 = c ´ c 4 13
4MN 2 =c ´ c, AC 2 =(c-0)(c-0)=c ´ c, todėl 4MN 2 = AC 2 arba 2MN=AC vektorių MN ir AC kolineariškumo sąlyga (8) taip pat tenkinama , todėl MN ║AC. Talio teorema (įrodyta autoriaus)
Teorema
. Jei vienoje kampo pusėje lygiagrečios linijos nupjauna vienodus segmentus, tai kitoje kampo pusėje jos nupjauna vienodus segmentus. Įrodymas Tarkime, kad c=kb. Tada, jei BD||CE, tada turime (b-d)(´ c − 2 ´ d ¿= (´ b − ´ d) (c − 2d) Skliaustų atidarymas ir atvedimas panašius terminus, gauname lygtį b ´ c − 2 b ´ d −´ c d = ´ b c − 2 ´ b d − c ´ d Pakeitę c į kb ir ´ c į k ´ b , gausime bk ´ b -2b ´ d -dk ´ b = ´ b kb-2 ´ b d-kb ´ d . Vėl suvedę panašius terminus ir viską perkeldami į vieną pusę, gauname 2b ´ d + dk ´ b − 2 ´ b d − kb ´ d =0. Išimsime bendras daugiklis ir gauname 2(b ´ d − ´ b d ¿+ k (´ b d − b ´ d) = 0. Taigi k=2, t.y. c=2b. Panašiai įrodyta, kad f=3b ir tt Pitagoro teorema ( įrodė autorius) B stačiakampis trikampis hipotenuzės kvadratas lygi sumai kvadratinės kojos 14
Įrodymas. Atstumas tarp taškų B ir C lygus BC=|b-c|=b, BC 2 =b ´ b. Nuo |z| 2 = z ´ z , tada AC 2 =(a-c)(c ´ a − ´ ¿ ¿=(a − 0) (´ a - 0)=a ´ a . AB 2 =(a-b)(´ a − ´ b ¿= a ´ a − a ´ b - ´ a b+b ´ b Kadangi b yra tikrasis skaičius, ty b= ´ b , tai -a ´ b =− ab , tai a = - ´ a, tai yra - ´ ab = ab tiesė (įrodyta autoriaus) Įrodykime, kad trikampio ortocentras, centroidas ir cirkumcentras yra toje pačioje tiesėje (ši tiesė vadinama Eilerio tiese), o OG = 1/2GH 15.
Įrodymas: Taškas G(g) yra trikampio ABC centroidas, H(h) yra stačiakampis, o O(o) yra trikampio apibrėžtojo apskritimo centras. Kad šie taškai būtų kolinearūs, turi būti įvykdyta lygybė (10): (g-о)(´ g - ´ h ¿ -(´ g − ´ o ¿ (g − h) =0) Tašką O laikykime kaip kilmė, tada g(´ g - ´ h ¿ - ´ g (g − h) =g 2 -g ´ h −¿ (g 2 - h ´ g ¿ =-g ´ h + h ´ g (30) Ortocentro kompleksinė koordinatė apskaičiuojama pagal formulę (24) h=a+b+c, (30a), o centroidas pagal formulę (23) g = 1 3 (a + b + c) (30c) Pakeiskite į ( 30), gauname 1 3 (a+b +c)(´ a + b + c)-(a+b+c)(´ a + b + c 1 3 ¿))=0 (10). tenkinama, todėl apibrėžtojo trikampio centroidas, ortocentras ir centras yra toje pačioje tiesėje OG=g= 1 3 (a+b+c) GH=h-g=a+b+c- 1 3 (a. +b+c)= 2 3 (a+b+c) Gavome, kad OG= 1 2 GH Teorema įrodyta 16.
Eulerio apskritimas (devynių taškų apskritimas). Įrodė autorius. Apsvarstykite trikampį ABC. Sutikime, kad | OA | = | OB |= | OC | =1, t.y. visos trikampio viršūnės priklauso vienetiniam apskritimui z ´ z = 1 (apskritimo centras O yra pradžia, o spindulys yra ilgio vienetas). Įrodykime, kad pagrindai turi tris aukščius
savavališkas trikampis
, jo trijų kraštinių vidurio taškai ir trijų atkarpų, jungiančių jos viršūnes su stačiakampiu, vidurio taškai yra tame pačiame apskritime, o jo centras yra atkarpos OH vidurio taškas, kur H, prisiminimas, yra trikampio ABC stačiakampis. Toks ratas vadinamas
Nes trikampis ABC įrašytas į apskritimą z ´ z = 1, tada | a | = | b | = | c | = 1,→ | a 2 | = | b 2 | = | c 2 | = 1 2 | a || b | | c | = 1 2 | a || c | | b | = 1 2 | b || c | | a | = 1 2 Taigi taškai D, E, F, K, L, M, N, Q, F priklauso tam pačiam apskritimui Gauso teorema Jei tiesė kerta tieses, turinčias atitinkamai trikampio ABC kraštines BC, CA, AB, taškai A 1, B 1 , C 1, tada atkarpų AA 1, BB 1, СС 1 vidurio taškai yra kolinearūs. Naudodamiesi (11), užrašome taškų AB 1 C, CA 1 B, BC 1 A, A 1 B 1 C 1 tripletų kolineariškumo sąlygas: 0,) b - a (c) a - c () c - b (a 0 ,) c - b a() b - a () a - c b(0,) a - c b() c - b () b - a c(0,) b - a (c) a - c () c - b a (1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 b c a b, (31, P) vidurys atkarpas AA 1, BB 1, CC 1, tada turime parodyti, kad 0) () () ( n m p m p n p n m (32) Nuo), (2 1), (2 1), (2 1) 1 1 1 c c p b b n a a m tada įrodinėjama lygybė (31) yra lygiavertė: 0))(())(())((1 1 1 1 1 1 1 1 1 ) b b a a c c a c c b c c b b a a arba padauginus: 0) () () () () () () () () () () () (1 1 1) 1 1 1 1 1 1 1 1 a c b a su b a c b a c a c b a su b a c b a c b c b a c b a c b a c a (33) Dabar lengva suprasti, kad (33) gaunamas terminais pridedant lygybes (31). Įrodymas baigtas
IV skyrius.
USE uždavinių ir įvairių olimpiadų sprendimas kompleksinių skaičių metodu.
1 uždavinys. Vieningas valstybinis egzaminas -2012, P-4 Tiesėje, kurioje yra stačiojo trikampio ABC su stačiu kampu C mediana AD, imamas taškas E, nutolęs nuo viršūnės A atstumu, lygiu 4. Raskite plotą trikampis BCE, jei BC = 6, AC = 4. Pirmas sprendimas. Pagal Pitagoro teoremą AD=5. Tada ED=1 Tegul taškas E yra ant spindulio AD. Mediana AD yra ilgesnė už AE, o taškas E yra trikampio ABC viduje (1 pav.) Numeskime statmeną EF iš taško E į tiesę BC ir apsvarstykime panašius stačiuosius trikampius DEF ir DAC. Iš šių trikampių panašumo gauname: EF = AC ∙ ED AD = 4 5 19
Todėl S BCE = 1 2 ∙ 6 ∙ 4 5 = 2,4. Tegu dabar taškas A yra tarp E ir D (2 pav.). Šiuo atveju ED=9 ir EF = AC ∙ ED AD = 36 5 . Tada S BCE = 1 2 ∙ 6 ∙ 36 5 = 21,6. Atsakymas: 2,4; 21.6. Problemos sprendimas naudojant kompleksinius skaičius. I atvejis: taškas E yra ant spindulio AD. Kadangi D yra CB vidurys, tai CD=3. O kadangi CA=4, tai aišku, kad AD=5, t.y. DE=1. Paimkime tašką C kaip pradinį tašką, o tieses CA ir CB kaip realią ir įsivaizduojamą ašis. Tada A(4), C(0), B(6i), D(3i), E(e). Taškai A, E ir D yra kolinearūs, tada e − 4 3i − e = 4 t.y. e= 12i + 4 5 . Pagal (25) formulę S CBE =│ ´ i 4 (e6 ´ i +6i(− ´ e)│= e e − ´ ¿ 6 i 2 4 ¿ ¿ =2.4 II atvejis: taškas A yra tarp taškų D ir E , tada 4 − e 3i − 4 = 4 5, t.y. e= 36 − 12 i 5 S CBE = | 3 i 2 2 (36 − 12 i 5 − − 36 − 12i 5) : 2.4 ir 21.6 Pirmuoju būdu reikia turėti keletą spėjimų, kurie gali pasirodyti ne iš karto, o po gana ilgo samprotavimo Antras būdas, mes naudojame paruoštas formules, taupydami laiką, tačiau nežinant formulių, sudėtingų skaičių metodu uždaviniai negali būti išspręsti, kaip matote, kiekvienas metodas turi savo privalumų .
2 užduotis (MIOO, 2011):
„Taškas M yra atkarpoje AB. Ant apskritimo, kurio skersmuo AB, imamas taškas C, nutolęs nuo taškų A, M ir B atitinkamai 20, 14 ir 15 atstumu. Raskite trikampio BMC plotą." 20
Sprendimas: Kadangi AB yra apskritimo skersmuo, tai ∆ ABC yra stačiakampis, ∠ C = 90 ° Laikykime C kaip nulinis taškas plokštuma, tada A(20i), B(15), M(z). Kadangi CM=14, galioja lygybė z ´ z = 196, ty taškas M ∈ apskritimas, kurio centras yra taške C, o r=14. Raskime šio apskritimo susikirtimo taškus su tiese AB: Tiesės AB (10a) lygtis: 20 i (15 −´ z) + 15 (´ z + 20 i) + z (− 20 i − 15) = 0 Keičiant ´ z su 196 z ir padauginus visą lygtį iš (4 i − 3) gauname kvadratinę z lygtį: 25 z 2 + 120 i (4 i − 3) z + 196 (4 i − 3) 2 = 0 z 1,2 = 2 (3 − 4 i) (6 i± √ 13) 5 Naudodami (28) formulę randame plotą ∆ MBC: S = i 4 (z (´ b − ´ c) + b (´ c) −´z) + c (´z −´´ b)) kur c = 0, ´c = 0, b = 15, ´b = 15, ´z = 196 ∗ 5 2 (3 − 4 i) (6 i ± √ 13) Baigę lygiavertės transformacijos, gauname S = 54 ± 12 √ 13 kv. vienetų Atsakymas. 54 ± 12 √ 13 kv. vienetų Jei išspręsite problemą geometriniai metodai, tuomet reikia nagrinėti du skirtingus atvejus: 1-asis - taškas M yra tarp A ir D; 2 - tarp D ir B. 21
Sprendžiant uždavinį kompleksinių skaičių metodu, sprendimo dvilypumas gaunamas dėl to, kad yra du apskritimo ir tiesės susikirtimo taškai. Ši aplinkybė leidžia išvengti dažnos klaidos.
3 problema
Trikampio ABC medianos AA 1, BB 1 ir CC 1 susikerta taške M. Yra žinoma, kad AB=6MC 1. Įrodykite, kad trikampis ABC yra stačiakampis. Sprendimas: Tegul C yra nulinis plokštumos taškas, o taškui A priskirkite tikrąjį vienetą. Tada problema redukuojama iki įrodymo, kad b yra grynai įsivaizduojamas skaičius. AB 2 = (b − 1) (´ b − 1) . M yra centroidas, jo koordinatė yra 1 3 b + 1 3 MC 1 2 = (1 3 b + 1 3 − 1 2 b − 1 2)(1 3 ´ b + 1 3 − 1 2 ´ b − 1 2) = 1 3 b (b + 1) (´ b + 1) Kadangi AB=6MC 1, tai (b − 1) (´ b − 1) = (b + 1) (´ b + 1) . Atlikę transformacijas gauname b =− ´ b, t.y. b yra grynai įsivaizduojamas skaičius, t.y. kampas C yra tiesė.
4 užduotis.
22
Dėl 90° apsisukimo aplink tašką O atkarpa AB virto atkarpa A "B". Įrodykite , kad trikampio OAB " mediana OM yra statmena tiesei A " B . Sprendimas: Tegul koordinatės O, A, B yra lygios atitinkamai 0,1, b. Tada taškai A " ir B " turės koordinates a" = i ir b" = bi, o atkarpos AB " vidurio M koordinates m = 1 2 (1 + bi). Randame: a " − b m − 0 = i − b 1 2 (1 + bi) = 2 i (i − b) i − b = 2i skaičius yra grynai įsivaizduojamas. Remiantis statmenumo kriterijumi (atkarpos AB ir CD yra statmenos tada ir tik tada, kai skaičius a − b c − d yra grynai įsivaizduojamas), tiesės OM ir A ’ B yra statmenos.
5 problema
.
23
Nuo trikampio aukščio pagrindo statmenai nuleidžiami į dvi puses, kurios neatitinka šio aukščio. Įrodykite, kad atstumas tarp šių statmenų pagrindų nepriklauso nuo trikampio aukščio pasirinkimo. Sprendimas: Tegu pateikiamas trikampis ABC, o aplink jį apibrėžtas apskritimas turi lygtį z ´ z = 1. Jei CD yra trikampio aukštis, tai d = 1 2 (a + b + c − ab c) Statmenų, atitinkamai numetusių iš taško D į AC ir BC, kompleksinės koordinatės yra lygios m = 1 2 (a + c + d − ac´ d 2) n = 1 2 (b + c + d − bc´ d 2) Randame: m − n = 1 2 (a − b + c´ d ( b − a)) = 1 2 ( a − b) (1 − c ´ d) = (a − b) (a − c) (b − c) 4 ab Kadangi | a | = | b | = 1, tada | m − n | = | (a − b) × (b − c) (c − a) | 4. Ši išraiška yra simetriška a, b, c atžvilgiu, t.y. atstumas MN nepriklauso nuo trikampio aukščio pasirinkimo.
Išvada
24
"Žinoma! Visas problemas galima išspręsti be kompleksinių skaičių. Tačiau faktas yra tas, kad kompleksinių skaičių algebra yra kita efektyvus metodas planimetrinių uždavinių sprendimas. Galime kalbėti tik apie efektyvesnio metodo pasirinkimą konkrečiai užduočiai atlikti. Ginčai dėl konkretaus metodo pranašumų yra beprasmiai, jei šiuos metodus nagrinėsime apskritai, netaikant konkrečios problemos“ [2]. Didelę vietą metodo tyrime užima formulių rinkinys. Tai yra
pagrindinis trūkumas
metodu ir tuo pačiu
orumo
, nes tai leidžia išspręsti pakankamai sudėtingos užduotys pagal paruoštas formules su elementariais skaičiavimais. Be to, manau, kad sprendžiant planimetrijos uždavinius šis metodas yra universalus.
Bibliografija
1. Markushevich A.I. Sudėtiniai skaičiai ir konforminiai atvaizdai - M.: Valstybinė techninės ir teorinės literatūros leidykla, 1954. - 52 p. 25
2. Ponarin Ya. P. Geometrinių uždavinių kompleksinių skaičių algebra: Knyga mokyklų matematinių klasių studentams, mokytojams ir pedagoginių universitetų studentams - M.: MTsNMO, 2004. - 160 p. 3. Shvetsov D. Nuo Simsono linijos iki Droz-Farny teoremos, Kvant. - Nr.6, 2009. – p. 44-48 4. Yaglom I. M. Geometrinės transformacijos. Tiesinės ir apskritos transformacijos. - Valstybinė techninės ir teorinės literatūros leidykla, 1956. – 612 p. 5. Yaglom I.M. Kompleksiniai skaičiai ir jų taikymas geometrijoje - M.: Fizmatgiz, 1963. - 192 p. 6. Morkovich A.G. ir kiti, Algebra ir matematinės analizės pradžia 10 kl. Per 2 valandas 1 dalis. Vadovėlis bendrojo ugdymo įstaigų mokiniams (profilinis lygis) - M.: Mnemosyne, 2012. - 343 p. 7. Andronovas I.K. Realiųjų ir kompleksinių skaičių matematika - M.: Prosveshchenie, 1975. - 158 p. 26
Taikymas
Klasikinės elementariosios geometrijos teoremos
Niutono teorema.
Keturkampyje, apibrėžtame apie apskritimą, įstrižainių vidurio taškai yra tiesūs su apskritimo centru. 27
Įrodymas. Pradėkime nuo apskritimo centro, nustatydami jo spindulį lygų vienetui. Šio keturkampio trikampio A o B o C o D o kraštinių sąlyčio taškus pažymėkime A, B, C, D (apvalia tvarka) (4 pav.). Tegu M ir N yra atitinkamai įstrižainių A o C o ir B o D o vidurio taškai. Tada pagal apskritimo liestinių susikirtimo taškų formulę z = 2ab a + b, taškai A o , B o , C o , D o turės atitinkamai kompleksines koordinates: , 2 , 2 , 2 , 2 0 0 0 0 d c cd d c b bc c b a ab b d a ad a čia a, b, c, d yra kompleksinės taškų A, B, C, D koordinatės. Todėl.) (2 1 ,) (2 1 0 0 0 d c cd b a ab d b n c b bc d a ad c a m b. b Kadangi, 1 , 1 b b a a , 1 , 1 d d c c tada tiesiogiai aišku, kad n m n m Remiantis (6), taškai O, M, N yra kolinearūs.
Paskalio teorema
.
Tiesių, turinčių priešingas įbrėžto šešiakampio puses, susikirtimo taškai yra toje pačioje tiesėje. 28
Įrodymas. Tegu šešiakampis ABCDEF ir P FA CD N EF BC M DE AB ) () (,) () (,) () ( (6 pav.) įbrėžtas apskritime (6 pav.). Apskritimo centrą laikykime plokštumos nuliniu tašku, o jo spindulys yra ilgio vienetui. Tada pagal (17) gauname: ,) (,) (,) (fa cd a f d c p ef bc f e c b n). de ab e d b a m Apskaičiuoti) )())(ef bc de ab ab fa ef ir panašiai .))(())((fa cd ef bc bc ab fa ef de cd f c p n Toliau randame: .))())((de ab c f fa cd n e) Kadangi skaičiai f e d c b a yra lygūs, atitinkamai, f e d c b a 1 , 1 , 1 , 1, 1, 1, tai patikrinus žodžiu paaiškėja, kad rasta išraiška sutampa su jos konjugatu, tai yra tikrasis skaičius. Tai reiškia, kad taškai M, N, P yra kolinearūs.
Monge'o teorema.
Keturkampyje, įbrėžtame į apskritimą, tiesės, einančios per kraštinių vidurio taškus ir. Kiekviena įstrižainė yra statmena priešingoms kraštinėms ir atitinkamai kita įstrižainė susikerta viename taške. Jis vadinamas ciklinio keturkampio Monge tašku. Įrodymas. Statmenys keturkampio ABCD kraštinėms susikerta apskritimo centre, kurį laikome pradiniu tašku. Kiekvienam taškui M(z) statmenas bisektoriusį [AB] skaičių b a b a z ) (2 1 grynai įsivaizduojamas. 29
Konkrečiai, jei z=0, jis yra lygus) (2) (b a b a . Kiekviename tiesės, einančios per (AB) statmenos kraštinės CD vidurį, N(z) skaičius b a d c z ) (2 1 turės būti grynai įsivaizduojamas ir atvirkščiai. Bet z=) (2 1 d c b a jis lygus) (2 b a b a t.y. grynai įsivaizduojamas. Todėl taškas E su kompleksine koordinate) (2 1 d c b a yra ant nurodytos linijos Ir ši išraiška yra simetriška raidžių a, b, c, d atžvilgiu. Todėl kitose penkiose panašiai sukonstruotose eilutėse yra taškas E. 30
GALIMYBĖ NAUDOTI KOMPLEKSINIUS SKAIČIUS
MATEMATIKOS KURSAS BENDROJO UGDYMO MOKYKLOJE
Mokslinis vadovas:
Savivaldybės švietimo įstaiga
Pervomaiskajos vidurinė mokykla
Su. Kichmengsky miestas
Šv. Zarechnaya 38
Pateikiamas darbas skirtas kompleksinių skaičių tyrinėjimui. Aktualumas: sprendžiant daugelį fizikos ir technologijų problemų, gaunamos kvadratinės lygtys su neigiamas diskriminatorius. Šios lygtys neturi sprendimo šiame regione realūs skaičiai. Tačiau daugelio tokių problemų sprendimas turi labai apibrėžtą fizinę prasmę.
Praktinė reikšmė: sudėtingi skaičiai ir sudėtingų kintamųjų funkcijos naudojami daugelyje mokslo ir technologijų klausimų, kuriuos galima naudoti mokykloje kvadratines lygtis.
Objekto plotas: matematika. Tyrimo objektas: algebrinės sąvokos ir veiksmus. Tyrimo objektas– kompleksiniai skaičiai. Problema: matematikos kursuose kompleksiniai skaičiai nemokami vidurinę mokyklą, nors jie gali būti naudojami kvadratinėms lygtims spręsti. Galimybė įvesti kompleksinius skaičius Vieningų valstybinių egzaminų užduotys ateityje. Hipotezė: Sudėtinius skaičius galite naudoti norėdami išspręsti kvadratines lygtis vidurinėje mokykloje. Tikslas: ištirti kompleksinių skaičių vartojimo galimybę mokantis matematikos vidurinės mokyklos 10 klasėje. Užduotys: 1. Studijuokite kompleksinių skaičių teoriją. 2. Apsvarstykite galimybę panaudoti kompleksinius skaičius 10 klasės matematikos kurse. 3. Kurti ir išbandyti užduotis su kompleksiniais skaičiais.
Norėdami išspręsti algebrines lygtis Nėra pakankamai realių skaičių. Todėl natūralu stengtis, kad šios lygtys būtų išsprendžiamos, o tai savo ruožtu veda prie skaičiaus sąvokos išplėtimo..gif" width="10" height="65 src=">
https://pandia.ru/text/78/027/images/image005_18.gif" width="10" height="62">.gif" width="97" height="28 src=">
tereikia sutikti veikti pagal tokias išraiškas pagal įprastos algebros taisykles ir manyti, kad ![]()
1572 metais buvo išleista italų algebristo R. Bombelli knyga, kurioje buvo nustatytos pirmosios aritmetinių veiksmų su tokiais skaičiais taisyklės iki ištraukimo iš jų. kubinės šaknys. Pavadinimas „įsivaizduojami skaičiai“ buvo įvestas 1637 m. Prancūzų matematikas ir filosofas R. Dekartas, o 1777 m. – vienas didžiausių VIII amžiaus matematikų X..gif" width="58" height="19"> kaip kompleksinių skaičių naudojimo matematikos studijose pavyzdys. 10 klasėje vadinasi skaičius x, kurio kvadratas yra –1 įsivaizduojamas vienetas ir žymimas i. Taigi, kur yra ..gif" width="120" height="27 src=">.gif" width="100" height="27 src=">8th class" href="/text/category/8_klass / " rel="bookmark">8 klasės algebra. - M.: Išsilavinimas, 1994.-P.134-139.
2. Enciklopedinis žodynas jaunasis matematikas / Comp. E-68. - M.: Pedagogika, 19с
- Remsimės ryšiais, o ne mechaninėmis formulėmis.
- Apsvarstykime kompleksinius skaičius kaip mūsų skaičių sistemos papildymą, kaip ir nulį, trupmeninius ar neigiamus skaičius.
- Idėjas vizualizuojame grafikoje, kad geriau suprastume esmę, o ne tik jas pateikiame sausu tekstu.
Ir mūsų slaptas ginklas: mokymasis pagal analogiją. Prie kompleksinių skaičių pasieksime pradėdami nuo jų protėvių, neigiamų skaičių. Štai jums mažas vadovas:
Kol kas ši lentelė mažai prasminga, bet tebūnie. Straipsnio pabaigoje viskas atsistos į savo vietas.
Iš tikrųjų supraskime, kas yra neigiami skaičiai
Neigiami skaičiai nėra taip paprasta. Įsivaizduokite, kad esate XVIII amžiaus Europos matematikas. Turite 3 ir 4 ir galite parašyti 4 – 3 = 1. Tai paprasta.
Bet kas yra 3–4? Ką tai tiksliai reiškia? Kaip galima atimti 4 karves iš 3? Kaip gali turėti mažiau nei nieko?
Neigiami skaičiai buvo laikomi visiška nesąmonė, o tai „metė šešėlį visai lygčių teorijai“ (Francis Maceres, 1759). Šiandien tai būtų visiška nesąmonė galvoti apie neigiamus skaičius kaip apie kažką nelogiško ir nenaudingo. Paklauskite savo mokytojo, ar neigiami skaičiai pažeidžia pagrindinę matematiką.
Kas atsitiko? Išradome teorinį skaičių, kuris turėjo naudingų savybių. Neigiami skaičiai negali būti paliesti ar pajausti, bet jie puikiai apibūdina tam tikrus santykius (pavyzdžiui, skolą). Tai labai naudinga idėja.
Užuot sakęs: „Esu jums skolingas 30“ ir skaitydamas žodžius, kad pamatyčiau, ar man netrūksta, ar ne, galiu tiesiog užsirašyti „-30“ ir žinoti, ką tai reiškia. Jei užsidirbu pinigų ir apmokėsiu skolas (-30 + 100 = 70), galiu lengvai parašyti šią operaciją keliais simboliais. Man liks +70.
Pliuso ir minuso ženklai automatiškai fiksuoja kryptį – nereikia viso sakinio, kad apibūdintumėte pokyčius po kiekvienos operacijos. Matematika tapo paprastesnė, elegantiškesnė. Jau nebesvarbu, ar neigiami skaičiai yra „apčiuopiami“ – jie turi naudingų savybių, ir naudojome juos tol, kol jie tvirtai įsitvirtino mūsų kasdieniame gyvenime. Jei kas nors, ką pažįstate, dar nesuprato neigiamų skaičių esmės, dabar jūs jam padėsite.
Tačiau nesumažinkite žmonių kančių: neigiami skaičiai buvo tikras sąmonės pokytis. Netgi Euleris, genijus, atradęs skaičių e ir daug daugiau, neigiamų skaičių nesuprato taip gerai, kaip mes šiandien. Jie buvo vertinami kaip „beprasmiai“ skaičiavimų rezultatai.
Keista tikėtis, kad vaikai ramiai supras mintis, kurios kadaise supainiojo net geriausius matematikus.
Įsivaizduojamų skaičių įvedimas
Ta pati istorija su įsivaizduojamais skaičiais. Šias lygtis galime išspręsti visą dieną:
Atsakymai bus 3 ir -3. Bet įsivaizduokime, kad koks nors protingas vaikinas čia pridėjo minusą:
![]()
Na, gerai. Tai toks klausimas, dėl kurio žmonės susigūžta, kai pamato jį pirmą kartą. Ar norite apskaičiuoti skaičiaus, mažesnio už nulį, kvadratinę šaknį? Tai neįsivaizduojama! (Istoriškai tokių tikrai buvo panašius klausimus, bet man patogiau įsivaizduoti kokį beveidį išmintingą žmogų, kad nesudarytų gėdos praeities mokslininkams).
Atrodo beprotiškai, kaip neigiami skaičiai, nulis ir neracionalūs skaičiai (nepasikartojantys skaičiai) žiūrėjo atgal. Šis klausimas neturi „tikrosios“ prasmės, tiesa?
Ne, tai netiesa. Vadinamieji „įsivaizduojami skaičiai“ yra tokie pat normalūs kaip ir bet kurie kiti (arba tokie pat nenormalūs): jie yra pasaulio apibūdinimo įrankis. Ta pačia dvasia, kurią įsivaizduojame, kad -1, 0,3 ir 0 "egzistuoja", tarkime, kad yra skaičius i, kur:
![]()
Kitaip tariant, padauginkite i iš savęs, kad gautumėte -1. Kas dabar vyksta?
Na, iš pradžių mums tikrai skauda galvą. Tačiau žaisdami žaidimą „Apsimeskime, kad aš egzistuoju“ matematiką darome paprastesnę ir elegantiškesnę. Atsiranda naujų ryšių, kuriuos galime lengvai apibūdinti.
Nepatikėsite i, kaip ir tie seni rūstūs matematikai netikėjo -1 egzistavimu. Visos naujos sąvokos, kurios susuka smegenis į vamzdelį, yra sunkiai suvokiamos, o jų prasmė iškyla ne iš karto, net ir genialiajam Euleriui. Tačiau, kaip parodė neigiami skaičiai, keistos naujos idėjos gali būti labai naudingos.
Man nepatinka pats terminas „įsivaizduojami skaičiai“ – atrodo, kad jis buvo pasirinktas specialiai tam, kad įžeistų i jausmus. Skaičius i yra toks pat normalus kaip ir kiti, bet prie jo prilipo slapyvardis „įsivaizduojamas“, tad jį taip pat naudosime.
Vizualus neigiamų ir kompleksinių skaičių supratimas
Lygtis x^2 = 9 iš tikrųjų reiškia tai:
![]()
Kuri x transformacija, taikoma du kartus, paverčia 1 į 9?
Yra du atsakymai: "x = 3" ir "x = -3". Tai reiškia, kad galite „paskirstyti pagal“ 3 kartus arba „paskirstyti 3 ir apversti“ (rezultato apvertimas arba atsakomosios vertės paėmimas yra daugybos iš neigiamo vertės interpretacijos).
Dabar pagalvokime apie lygtį x^2 = -1, kurią galima parašyti taip:
Kuri x transformacija, taikoma du kartus, paverčia 1 į -1? Hm.
- Mes negalime padauginti du kartus teigiamas skaičius nes rezultatas bus teigiamas.
- Negalime neigiamo skaičiaus padauginti du kartus, nes rezultatas vėl bus teigiamas.
Ką jau kalbėti apie... rotaciją! Žinoma, tai skamba neįprastai, bet ką daryti, jei x laikysime „90 laipsnių pasukimą“, tada taikydami x du kartus padarysime 180 laipsnių pasukimą koordinačių ašis, o 1 pavirs į -1!

Oho! Ir jei pagalvosime apie tai šiek tiek daugiau, galime padaryti dvi revoliucijas priešinga kryptimi, taip pat pereikite nuo 1 iki -1. Tai yra „neigiamas“ pasukimas arba daugyba iš -i:
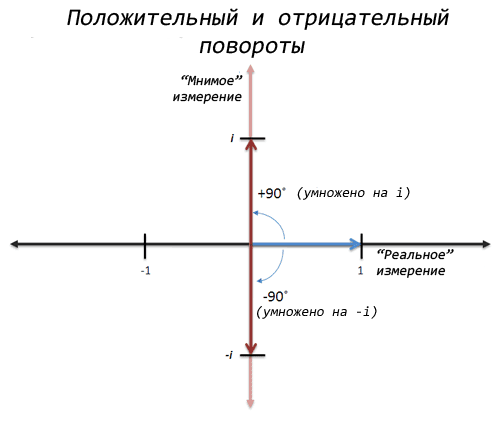
Jei padauginsime iš -i du kartus, tai per pirmąjį dauginimą gausime -i iš 1, o antruoju -1 iš -i. Taigi iš tikrųjų yra du kvadratinės šaknys-1: i ir -i.
Tai labai šaunu! Turime kažką panašaus į sprendimą, bet ką tai reiškia?
- i yra "nauja įsivaizduojama dimensija" skaičiui matuoti
- i (arba -i) yra tai, kuo skaičiai „tampa“, kai juos pasukame
- Padauginus iš i, sukasi 90 laipsnių prieš laikrodžio rodyklę
- Padauginus iš -i yra sukimasis 90 laipsnių pagal laikrodžio rodyklę.
- Sukant du kartus bet kuria kryptimi gaunamas -1: tai grąžina mus į „įprastą“ teigiamų ir neigiamų skaičių dimensiją (x ašį).
Visi skaičiai yra dvimačiai. Taip, sunku tai priimti, bet senovės romėnams būtų buvę taip pat sunku tai priimti. po kablelio arba ilgasis padalijimas. (Kaip tai, kad yra daugiau skaičių tarp 1 ir 2?). Keistai atrodo kaip bet kas naujas būdas mąstyti matematikoje.
Mes paklausėme "Kaip dviem veiksmais 1 paversti į -1?" ir rado atsakymą: pasukite 1 90 laipsnių du kartus. Gana keistas, naujas mąstymo būdas matematikoje. Bet labai naudinga. (Beje, tai geometrinė interpretacija kompleksiniai skaičiai atsirado tik praėjus dešimtmečiams po skaičiaus i atradimo).
Taip pat nepamirškite, kad apsisukimas prieš laikrodžio rodyklę yra teigiamas rezultatas– tai grynai žmogiškas susitarimas, ir viskas galėjo būti visiškai kitaip.
Ieškoti rinkinių
Pasigilinkime į smulkmenas. Kai padauginate neigiamus skaičius (pvz., -1), gausite rinkinį:
- 1, -1, 1, -1, 1, -1, 1, -1
Kadangi -1 nekeičia skaičiaus dydžio, tik ženklą, jūs gaunate tą patį skaičių arba su „+“ ženklu, arba su „-“ ženklu. Už skaičių x gausite:
- x, -x, x, -x, x, -x…
Tai labai naudinga idėja. Skaičius „x“ gali reikšti geras ir blogas savaites. Įsivaizduokime tai geros savaitės pakeičia blogą; Tai gera savaitė; Kokia bus 47-oji savaitė?
X reiškia, kad tai bus bloga savaitė. Pažiūrėkite, kaip neigiami skaičiai „seka ženklą“ – į skaičiuotuvą galime tiesiog įvesti (-1)^47, o ne skaičiuoti („1 savaitė gerai, 2 savaitė blogai... 3 savaitė gerai...“). Daiktus, kurie nuolat keičiasi, galima puikiai sumodeliuoti naudojant neigiamus skaičius.
Gerai, kas atsitiks, jei ir toliau dauginsime iš i?
![]()
Labai juokinga, šiek tiek supaprastinkime:
Čia yra tas pats dalykas, pateiktas grafiškai:

Ciklą kartojame kas 4 posūkį. Tai tikrai prasminga, tiesa? Bet kuris vaikas pasakys, kad 4 posūkiai į kairę yra tas pats, kas visai nesisukti. Dabar pailsėkite nuo įsivaizduojamų skaičių (i, i^2) ir pažiūrėkite į bendrą rinkinį:
- X, Y, -X, -Y, X, Y, -X, -Y…
Kaip tiksliai modeliuojami neigiami skaičiai veidrodinis vaizdas skaičiai, įsivaizduojami skaičiai gali modeliuoti viską, kas sukasi tarp dviejų matmenų „X“ ir „Y“. Ar kas nors, kas turi ciklinę, žiedinę priklausomybę – ar turite ką nors galvoje?
Suprasti sudėtingus skaičius
Reikia apsvarstyti dar vieną detalę: ar skaičius gali būti ir „tikras“, ir „įsivaizduojamas“?
Net neabejokite. Kas sakė, kad turime pasisukti lygiai 90 laipsnių? Jei stovėsime viena koja ant „tikrojo“ dimensijos, o kita – ant „įsivaizduojamo“, tai atrodys maždaug taip:

Mes esame ties 45 laipsnių žyma, kur tikroji ir menama dalys yra vienodos, o pats skaičius yra „1 + i“. Tai kaip dešrainis, kur yra ir kečupas, ir garstyčios – kas sakė, kad reikia rinktis vieną ar kitą?
Iš esmės galime pasirinkti bet kokį realių ir įsivaizduojamų dalių derinį ir iš viso to padaryti trikampį. Kampas tampa „sukimosi kampu“. Kompleksinis skaičius yra išgalvotas skaičių, turinčių tikrąją ir įsivaizduojamą dalis, pavadinimas. Jie rašomi kaip „a + bi“, kur:
- a - tikroji dalis
- b – įsivaizduojama dalis

Neblogai. Tačiau lieka vienas paskutinis klausimas: koks „didelis“ yra kompleksinis skaičius? Negalime išmatuoti tikrosios ar įsivaizduojamos dalies atskirai, nes praleisime bendrą vaizdą.
Ženkime žingsnį atgal. Neigiamojo skaičiaus dydis yra atstumas nuo nulio:
Tai dar vienas būdas rasti absoliuti vertė. Bet kaip kompleksiniams skaičiams išmatuoti abu komponentus 90 laipsnių kampu?
Ar tai paukštis danguje... ar lėktuvas... Pitagoras ateina į pagalbą!
Ši teorema pasirodo visur, kur įmanoma, net ir skaičiais, išrastais praėjus 2000 metų po pačios teoremos. Taip, mes darome trikampį, o jo hipotenuzė bus lygi atstumui nuo nulio:
Nors išmatuoti kompleksinį skaičių nėra taip paprasta, kaip „tik praleisti ženklą -“, kompleksiniai skaičiai turi labai daug naudingos programos. Pažvelkime į kai kuriuos iš jų.
Tikras pavyzdys: sukimai
Mes nelauksime, kol koledžo fizika mokysimės sudėtingų skaičių. Mes tai padarysime šiandien. Kompleksinių skaičių dauginimo tema galima pasakyti daug, tačiau kol kas turite suprasti pagrindinį dalyką:
- Padauginus iš kompleksinio skaičiaus, sukasi jo kampu
Pažiūrėkime, kaip tai veikia. Įsivaizduokite, kad esu valtyje ir judu 3 vienetų kursu į rytus kas 4 vienetus į šiaurę. Noriu pakeisti kursą 45 laipsniais prieš laikrodžio rodyklę. Koks bus mano naujas kursas?

Kas nors gali pasakyti: „Tai lengva! Apskaičiuokite sinusą, kosinusą, paieškokite google liestinės reikšmę... ir tada..." Manau, kad sugadinau skaičiuotuvą...
Eikime paprastesniu maršrutu: esame 3 + 4i kursu (nesvarbu koks kampas, mums dabar nesvarbu) ir norime apsisukti 45 laipsniais. Na, 45 laipsniai yra 1 + i (ideali įstrižainė). Taigi mes galime padauginti savo tarifą iš šio skaičiaus!

Štai esmė:
- Pradinė antraštė: 3 vienetai į rytus, 4 vienetai į šiaurę = 3 + 4i
- Pasukti prieš laikrodžio rodyklę 45 laipsnių = padauginti iš 1 + i
Padauginus gauname:

Mūsų naujoji gairė yra 1 vienetas į vakarus (-1 į rytus) ir 7 vienetai į šiaurę, galite nubrėžti koordinates grafike ir jomis vadovautis.
Bet! Atsakymą radome per 10 sekundžių, be sinusų ir kosinusų. Nebuvo nei vektorių, nei matricų, nei sekimo, kuriame kvadrante esame. Tai buvo paprasta aritmetika ir šiek tiek algebra, kad būtų galima sudaryti lygtį. Įsivaizduojami skaičiai puikiai tinka sukimuisi!
Be to, tokio skaičiavimo rezultatas yra labai naudingas. Vietoj kampo (atan(7/-1) = 98,13) turime kursą (-1, 7), ir iškart aišku, kad esame antrame kvadrante. Kaip tiksliai planavote braižyti ir laikytis nurodyto kampo ?
Ne, jūs konvertuotumėte kampą į kosinusą ir sinusą (-0,14 ir 0,99), rastumėte apytikslį jų santykį (apie 1:7) ir nubraižytumėte trikampį. Ir čia neabejotinai laimi kompleksiniai skaičiai – tiksliai, žaibiškai ir be skaičiuoklės!
Jei esate toks kaip aš, šis atradimas jums pribloškia. Jei ne, bijau, kad matematika jūsų visai nejaudina. Atsiprašau!
Trigonometrija yra gera, tačiau sudėtingi skaičiai labai palengvina skaičiavimus (pvz., rasti cos(a + b)). Tai tik mažas skelbimas; tolesniuose straipsniuose pateiksiu jums visą meniu.
Lyrinis nukrypimas: kai kurie žmonės galvoja maždaug taip: „Ei, nėra patogu krypti į šiaurę/rytus, o ne į paprastą kampą, kuriuo laivas galėtų sekti!
Ar tai tiesa? Gerai, pažiūrėk į savo dešine ranka. Koks kampas tarp mažojo piršto pagrindo ir galiuko rodomasis pirštas? Sėkmės taikant skaičiavimo metodą.
Arba galite tiesiog atsakyti: „Na, antgalis yra X colių į dešinę ir Y colių aukštyn“, ir galite ką nors padaryti.
Ar kompleksiniai skaičiai artėja?
Mano pagrindinius atradimus kompleksinių skaičių srityje išgyvenome kaip tornadas. Pažvelkite į pačią pirmąją iliustraciją, dabar ji turėtų tapti aiškesnė.
Dar daug ką galima atrasti šiuose gražiuose, nuostabiuose skaičiuose, bet mano smegenys jau pavargusios. Mano tikslas buvo paprastas:
- Įtikinkite jus, kad sudėtingi skaičiai buvo laikomi tik „beprotiškais“, bet iš tikrųjų jie gali būti labai naudingi (kaip ir neigiami skaičiai)
- Parodykite, kaip sudėtingi skaičiai gali supaprastinti kai kurias problemas, pvz., sukimąsi.
Jei man atrodo, kad ši tema pernelyg susirūpinusi, tam yra priežastis. Įsivaizduojami skaičiai buvo mano jau daugelį metų apsėdimas– Nesupratimas mane erzino.
Bet geriau uždegti žvakę, nei perbristi pilka tamsa: tai mano mintys ir esu tikras, kad ugnis užsidegs mano skaitytojų mintyse.
Epilogas: Bet jie vis tiek gana keisti!
Žinau, kad man jie vis dar atrodo keistai. Stengiuosi mąstyti kaip pirmasis žmogus, kuris atrado nulį minties.
Nulis yra tokia keista idėja, „kažkas“ reiškia „nieką“, ir to niekaip nepavyko suprasti Senovės Roma. Tas pats ir su kompleksiniais skaičiais – tai naujas mąstymo būdas. Tačiau tiek nuliniai, tiek kompleksiniai skaičiai labai supaprastina matematiką. Jei niekada nebūtume įvedę keistų dalykų, pavyzdžiui, naujų skaičių sistemų, vis tiek viską skaičiuotume ant pirštų.
Kartoju šią analogiją, nes taip lengva pradėti galvoti, kad kompleksiniai skaičiai yra „nenormalūs“. Būkime atviri naujovėms: ateityje žmonės tik juokaus apie tai, kaip kažkas iki XXI amžiaus netikėjo sudėtingais skaičiais.
2015 m. spalio 23 d







