વ્યાખ્યા 1. સંખ્યા અક્ષ (સંખ્યા રેખા, સંકલન રેખા) ઓક્સ એ સીધી રેખા છે જેના પર બિંદુ O પસંદ થયેલ છે મૂળ (કોઓર્ડિનેટ્સનું મૂળ)(ફિગ. 1), દિશા

ઓ → x

તરીકે યાદી થયેલ છે સકારાત્મક દિશાઅને એક સેગમેન્ટ ચિહ્નિત થયેલ છે, જેની લંબાઈ લેવામાં આવે છે લંબાઈનું એકમ.

વ્યાખ્યા 2. એક સેગમેન્ટ જેની લંબાઈ લંબાઈના એકમ તરીકે લેવામાં આવે છે તેને સ્કેલ કહેવામાં આવે છે.

સંખ્યા અક્ષ પર દરેક બિંદુ એક સંકલન ધરાવે છે, જે છે વાસ્તવિક સંખ્યા. બિંદુ O નો સંકલન શૂન્ય છે. ઓક્સ કિરણ પર પડેલા મનસ્વી બિંદુ A નું સંકલન OA સેગમેન્ટની લંબાઈ જેટલું છે.

આંકડાકીય અક્ષના એક મનસ્વી બિંદુ Aનું સંકલન જે કિરણ ઓક્સ પર નથી પડતું તે ઋણ છે, અને સંપૂર્ણ મૂલ્યમાં OA સેગમેન્ટની લંબાઈ જેટલું છે. વ્યાખ્યા 3.પ્લેન પર લંબચોરસ કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમ ઓક્સી બે પરસ્પર બોલાવોલંબ સંખ્યાત્મક અક્ષો Ox અને Oy સાથેસમાન સ્કેલ અનેસામાન્ય શરૂઆતકાઉન્ટડાઉન બિંદુ O પર, અને એવી રીતે કે કિરણ ઓક્સથી 90°ના ખૂણા પર કિરણ ઓય સુધીનું પરિભ્રમણ દિશામાં હાથ ધરવામાં આવે છેઘડિયાળની વિરુદ્ધ દિશામાં

(ફિગ. 2). નોંધ. આકૃતિ 2 માં બતાવેલ લંબચોરસ કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમ ઓક્સી કહેવાય છેજમણી સંકલન સિસ્ટમ , વિપરીતડાબી સંકલન સિસ્ટમો , જેમાં બીમ Oy ને 90° ના ખૂણા પર બીમ ઓક્સનું પરિભ્રમણ ઘડિયાળના કાંટાની દિશામાં કરવામાં આવે છે. આ માર્ગદર્શિકામાં અમેઅમે ફક્ત જમણા હાથની સંકલન પ્રણાલીઓને ધ્યાનમાં લઈએ છીએ

, ખાસ સ્પષ્ટ કર્યા વિના. જો આપણે પ્લેન પર લંબચોરસ કાર્ટેશિયન કોઓર્ડિનેટ્સ ઓક્સીની કેટલીક સિસ્ટમ દાખલ કરીએ, તો પ્લેનનો દરેક બિંદુ પ્રાપ્ત થશે – બે કોઓર્ડિનેટ્સસમાન સ્કેલ એબ્સીસાઓર્ડિનેટ , જે નીચે પ્રમાણે ગણવામાં આવે છે. પ્લેન પર A ને મનસ્વી બિંદુ બનવા દો. ચાલો બિંદુ A થી લંબ છોડીએ A.A. , જે નીચે પ્રમાણે ગણવામાં આવે છે. પ્લેન પર A ને મનસ્વી બિંદુ બનવા દો. ચાલો બિંદુ A થી લંબ છોડીએ 1 અને

2 થી સીધી રેખાઓ Ox અને Oy, અનુક્રમે (ફિગ. 3). વ્યાખ્યા 4. બિંદુ A નું એબ્સીસા એ બિંદુનું સંકલન છેએ વ્યાખ્યા 4. બિંદુ A નું એબ્સીસા એ બિંદુનું સંકલન છેનંબર અક્ષ Ox પર 1, બિંદુ A નું ઓર્ડિનેટ એ બિંદુનું સંકલન છે

નંબર અક્ષ પર 2 Oy. હોદ્દોબિંદુના કોઓર્ડિનેટ્સ (એબ્સિસા અને ઓર્ડિનેટ). A લંબચોરસમાંકાર્ટેશિયન સિસ્ટમ વ્યાખ્યા 4. બિંદુ A નું એબ્સીસા એ બિંદુનું સંકલન છે(x;ઓક્સિ કોઓર્ડિનેટ્સ (ફિગ. 4) સામાન્ય રીતે સૂચવવામાં આવે છે) y વ્યાખ્યા 4. બિંદુ A નું એબ્સીસા એ બિંદુનું સંકલન છે = (x; અથવા).

y નોંધ. બિંદુ O, કહેવાય છેમૂળ ઓ(0 ; 0) .

વ્યાખ્યા 5. લંબચોરસ કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમમાં ઓક્સી સંખ્યા અક્ષબળદને એબ્સીસા અક્ષ કહેવામાં આવે છે, અને સંખ્યાત્મક અક્ષ ઓયને ઓર્ડિનેટ અક્ષ (ફિગ. 5) કહેવામાં આવે છે.

વ્યાખ્યા 6. દરેક લંબચોરસ કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમ પ્લેનને 4 ક્વાર્ટર (ચતુર્થાંશ) માં વિભાજિત કરે છે, જેની સંખ્યા આકૃતિ 5 માં દર્શાવવામાં આવી છે.

વ્યાખ્યા 7. પ્લેન કે જેના પર લંબચોરસ કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમ આપવામાં આવે છે તેને કહેવામાં આવે છે સંકલન વિમાન.

નોંધ. એબ્સીસા અક્ષ પર સેટ કરેલ છે સંકલન વિમાનસમીકરણ અથવા= 0, સમીકરણ દ્વારા સંકલન સમતલ પર ઓર્ડિનેટ અક્ષ આપવામાં આવે છે x = 0.

વિધાન 1. બે બિંદુઓ વચ્ચેનું અંતરસંકલન વિમાન

વ્યાખ્યા 4. બિંદુ A નું એબ્સીસા એ બિંદુનું સંકલન છે 1 (x 1 ;ઓક્સિ કોઓર્ડિનેટ્સ (ફિગ. 4) સામાન્ય રીતે સૂચવવામાં આવે છે 1) સમાન સ્કેલ વ્યાખ્યા 4. બિંદુ A નું એબ્સીસા એ બિંદુનું સંકલન છે 2 (x 2 ;ઓક્સિ કોઓર્ડિનેટ્સ (ફિગ. 4) સામાન્ય રીતે સૂચવવામાં આવે છે 2)

ગણતરી કરેલ સૂત્ર અનુસાર

પુરાવો. આકૃતિ 6 ધ્યાનમાં લો.

આથી,

Q.E.D.

કોઓર્ડિનેટ પ્લેન પર વર્તુળનું સમીકરણ

ચાલો કોઓર્ડિનેટ પ્લેન ઓક્સી (ફિગ. 7) પર બિંદુ પર કેન્દ્ર સાથે ત્રિજ્યા Rનું વર્તુળ ધ્યાનમાં લઈએ. વ્યાખ્યા 4. બિંદુ A નું એબ્સીસા એ બિંદુનું સંકલન છે 0 (x 0 ;ઓક્સિ કોઓર્ડિનેટ્સ (ફિગ. 4) સામાન્ય રીતે સૂચવવામાં આવે છે 0) .

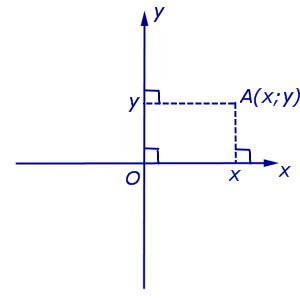
પ્લેન પર એક લંબચોરસ કોઓર્ડિનેટ સિસ્ટમ બે પરસ્પર લંબરૂપ સંકલન અક્ષો X’X અને Y’Y દ્વારા રચાય છે. સંકલન અક્ષો બિંદુ O પર છેદે છે, જેને મૂળ કહેવામાં આવે છે, દરેક અક્ષ પર એક સકારાત્મક દિશા પસંદ કરવામાં આવે છે (જમણા હાથની સંકલન પ્રણાલીમાં) જેથી જ્યારે X'X અક્ષને ફેરવવામાં આવે. 90° દ્વારા ઘડિયાળની વિરુદ્ધ દિશામાં, તેની હકારાત્મક દિશા Y'Y અક્ષની હકારાત્મક દિશા સાથે એકરુપ છે. સંકલન અક્ષો X'X અને Y'Y દ્વારા બનેલા ચાર ખૂણા (I, II, III, IV) ને સંકલન કોણ કહેવામાં આવે છે (જુઓ. આકૃતિ 1).

પ્લેન પર બિંદુ A ની સ્થિતિ બે કોઓર્ડિનેટ્સ x અને y દ્વારા નક્કી કરવામાં આવે છે. x કોઓર્ડિનેટ OB સેગમેન્ટની લંબાઈ જેટલો છે, y કોઓર્ડિનેટ માપનના પસંદ કરેલા એકમોમાં સેગમેન્ટ OCની લંબાઈ જેટલો છે. સેગમેન્ટ્સ OB અને OC અનુક્રમે Y'Y અને X'X અક્ષની સમાંતર બિંદુ A થી દોરેલી રેખાઓ દ્વારા વ્યાખ્યાયિત કરવામાં આવે છે. x કોઓર્ડિનેટને બિંદુ A નો એબ્સીસા કહેવામાં આવે છે, y કોઓર્ડિનેટને બિંદુ A નો ઓર્ડિનેટ કહેવામાં આવે છે. તે નીચે પ્રમાણે લખાયેલ છે: A(x, y).

જો બિંદુ A આવેલું છે સંકલન કોણ I, પછી બિંદુ A પાસે ધન એબ્સીસા અને ઓર્ડિનેટ છે. જો બિંદુ A સમન્વય કોણ II માં આવેલું છે, તો બિંદુ A ને નકારાત્મક એબ્સીસા અને હકારાત્મક ઓર્ડિનેટ ધરાવે છે. જો બિંદુ A સંકલન કોણ III માં આવેલું છે, તો બિંદુ A ને નકારાત્મક એબ્સીસા અને ઓર્ડિનેટ છે. જો બિંદુ A સમન્વય કોણ IV માં આવેલું હોય, તો બિંદુ A પાસે હકારાત્મક એબ્સીસા અને નકારાત્મક ઓર્ડિનેટ છે.

અવકાશમાં લંબચોરસ સંકલન સિસ્ટમત્રણ પરસ્પર લંબરૂપ સંકલન અક્ષ OX, OY અને OZ દ્વારા રચાય છે. સંકલન અક્ષો બિંદુ O પર છેદે છે, જેને મૂળ કહેવામાં આવે છે, દરેક અક્ષ પર હકારાત્મક દિશા પસંદ કરવામાં આવે છે, જે તીરો દ્વારા સૂચવવામાં આવે છે, અને અક્ષો પરના ભાગો માટે માપનનું એકમ. માપનના એકમો તમામ અક્ષો માટે સમાન છે. OX - abscissa axis, OY - ordinate axis, OZ - applicate axis. અક્ષોની હકારાત્મક દિશા પસંદ કરવામાં આવે છે જેથી જ્યારે OX અક્ષને 90° દ્વારા ઘડિયાળની વિરુદ્ધ દિશામાં ફેરવવામાં આવે, તો તેની સકારાત્મક દિશા OY અક્ષની સકારાત્મક દિશા સાથે એકરુપ હોય, જો આ પરિભ્રમણ OZ અક્ષની સકારાત્મક દિશામાંથી જોવામાં આવે. આવી સંકલન પ્રણાલીને જમણેરી કહેવામાં આવે છે. જો અંગૂઠો જમણો હાથ X દિશાને X દિશા તરીકે, અનુક્રમણિકાને Y દિશા તરીકે અને મધ્યને Z દિશા તરીકે લો, પછી જમણા હાથની સંકલન સિસ્ટમ રચાય છે. ડાબા હાથની સમાન આંગળીઓ ડાબી સંકલન પ્રણાલી બનાવે છે. જમણી અને ડાબી સંકલન પ્રણાલીઓને જોડવાનું અશક્ય છે જેથી અનુરૂપ અક્ષો એકરૂપ થાય (ફિગ. 2 જુઓ).

અવકાશમાં બિંદુ A ની સ્થિતિ ત્રણ કોઓર્ડિનેટ્સ x, y અને z દ્વારા નક્કી કરવામાં આવે છે. x કોઓર્ડિનેટ OB સેગમેન્ટની લંબાઈ જેટલો છે, y કોઓર્ડિનેટ એ સેગમેન્ટ OCની લંબાઈ છે, z કોઓર્ડિનેટ એ માપનના પસંદ કરેલા એકમોમાં સેગમેન્ટ ODની લંબાઈ છે. સેગમેન્ટ્સ OB, OC અને OD અનુક્રમે પ્લેન YOZ, XOZ અને XOY ના સમાંતર બિંદુ A થી દોરેલા પ્લેન દ્વારા વ્યાખ્યાયિત કરવામાં આવે છે. x કોઓર્ડિનેટને બિંદુ A નું એબ્સીસા કહેવામાં આવે છે, y કોઓર્ડિનેટને બિંદુ Aનું ઓર્ડિનેટ કહેવાય છે, z કોઓર્ડિનેટને બિંદુ Aનું અનુરૂપ કહેવામાં આવે છે. તે નીચે પ્રમાણે લખાયેલ છે: A(a, b, c).

ઓર્ટી

એક લંબચોરસ કોઓર્ડિનેટ સિસ્ટમ (કોઈપણ પરિમાણની) પણ એકમ વેક્ટરના સમૂહ દ્વારા વર્ણવવામાં આવે છે, જે સંકલન અક્ષો સાથે સહ-દિશામાં હોય છે. એકમ વેક્ટરની સંખ્યા કોઓર્ડિનેટ સિસ્ટમના પરિમાણ જેટલી છે અને તે બધા એકબીજાને લંબરૂપ છે.

ત્રિ-પરિમાણીય કિસ્સામાં, આવા એકમ વેક્ટર સામાન્ય રીતે સૂચવવામાં આવે છે i j k y ઇ x ઇ y ઇ z. વધુમાં, કિસ્સામાં યોગ્ય સિસ્ટમકોઓર્ડિનેટ્સ માન્ય છે નીચેના સૂત્રોવેક્ટરના ક્રોસ ઉત્પાદન સાથે:

• [i j]=k ;
• [j k]=i ;
• [k i]=j .

વાર્તા

લંબચોરસ સંકલન પ્રણાલી સૌપ્રથમ 1637 માં રેને ડેસકાર્ટેસ દ્વારા તેમના કાર્ય "પદ્ધતિ પર પ્રવચન" માં રજૂ કરવામાં આવી હતી. તેથી, લંબચોરસ સંકલન પ્રણાલીને પણ કહેવામાં આવે છે - કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમ. ભૌમિતિક વસ્તુઓનું વર્ણન કરવાની સંકલન પદ્ધતિએ પાયો નાખ્યો વિશ્લેષણાત્મક ભૂમિતિ. પિયર ફર્મટે પણ સંકલન પદ્ધતિના વિકાસમાં ફાળો આપ્યો હતો, પરંતુ તેમની કૃતિઓ તેમના મૃત્યુ પછી પ્રથમ પ્રકાશિત કરવામાં આવી હતી. ડેસકાર્ટેસ અને ફર્મેટે માત્ર પ્લેનમાં સંકલન પદ્ધતિનો ઉપયોગ કર્યો હતો.

માટે સંકલન પદ્ધતિ ત્રિ-પરિમાણીય જગ્યા 18મી સદીમાં લિયોનહાર્ડ યુલર દ્વારા સૌપ્રથમ ઉપયોગ કરવામાં આવ્યો હતો.

પણ જુઓ

લિંક્સ

વિકિમીડિયા ફાઉન્ડેશન.

• કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમ
• કાર્ટેશિયન ડિગ્રી

અન્ય શબ્દકોશોમાં "કાર્ટેશિયન કોઓર્ડિનેટ્સ" શું છે તે જુઓ:

કાર્ટેસિન કોઓર્ડિનેટ્સ- (કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમ) પ્લેન પર અથવા અવકાશમાં સંકલન સિસ્ટમ, સામાન્ય રીતે પરસ્પર લંબરૂપ અક્ષો અને લંબચોરસ અક્ષો સાથે સમાન ભીંગડા સાથે કાર્ટેશિયન કોઓર્ડિનેટ્સ. આર. ડેકાર્ટેસના નામ પરથી... મોટા જ્ઞાનકોશીય શબ્દકોશ

કાર્ટેશિયન કોઓર્ડિનેટ્સ- બે લંબ અક્ષો ધરાવતી સંકલન પ્રણાલી. આવી સિસ્ટમમાં બિંદુની સ્થિતિ બે સંખ્યાઓનો ઉપયોગ કરીને બનાવવામાં આવે છે જે દરેક અક્ષ સાથે સંકલન કેન્દ્રથી અંતર નક્કી કરે છે. માહિતીપ્રદ વિષયો......

કાર્ટેશિયન કોઓર્ડિનેટ્સટેકનિકલ અનુવાદકની માર્ગદર્શિકા - (કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમ), પ્લેન પર અથવા અવકાશમાં એક સંકલન સિસ્ટમ, સામાન્ય રીતે પરસ્પર લંબરૂપ અક્ષો અને લંબચોરસ કાર્ટેશિયન કોઓર્ડિનેટ્સ સાથે; આર. ડેકાર્ટેસના નામ પરથી...

કાર્ટેશિયન કોઓર્ડિનેટ્સજ્ઞાનકોશીય શબ્દકોશ - ડેકાર્ટો કોઓર્ડિનેટીસ સ્ટેટસ T sritis સ્ટેન્ડાર્ટિઝાસીજા ir મેટ્રોલોજીસ એપિબ્રેઝટિસ Tiesinė plokštumos arba erdvės koordinačių સિસ્ટમ. જોજે આશિઉ મસ્તેલીયા પાપ્રસ્તાય બુના લિગુસ. atitikmenys: engl. કાર્ટેશિયન કોઓર્ડિનેટ્સ વોક. kartesische Coordinaten, f…

કાર્ટેશિયન કોઓર્ડિનેટ્સ Penkiakalbis aiškinamasis metrologijos terminų žodynas

કાર્ટેસિન કોઓર્ડિનેટ્સ- Dekarto koordinatės statusas T sritis fizika atitikmenys: engl. કાર્ટેશિયન કોઓર્ડિનેટ્સ; ગ્રીડ કોઓર્ડિનેટ્સ વોક. kartesische Koordinaten, f rus. કાર્ટેશિયન કોઓર્ડિનેટ્સ, f pranc. coordonnées cartésiennes, f … Fizikos terminų žodynas - બે નિશ્ચિત કાટખૂણે સીધા અક્ષો સુધીના અંતર દ્વારા પ્લેન પરના બિંદુઓની સ્થિતિ નક્કી કરવાની પદ્ધતિ. આ ખ્યાલ પહેલાથી જ આર્કિમિડીઝ અને પેર્ગાના એપોલોજિસમાં બે હજાર વર્ષ પહેલાં અને પ્રાચીન ઇજિપ્તવાસીઓમાં પણ જોવા મળે છે. પ્રથમ વખત આ.......

કાર્ટેસિન કોઓર્ડિનેટ્સગાણિતિક જ્ઞાનકોશ - કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમ [ફ્રેન્ચના નામ પરથી નામ આપવામાં આવ્યું છે. ફિલસૂફ અને ગણિતશાસ્ત્રી આર. ડેસકાર્ટેસ (આર. ડેસકાર્ટેસ; 1596 1650)], પ્લેન અથવા અવકાશમાં એક સંકલન પ્રણાલી, સામાન્ય રીતે પરસ્પર લંબરૂપ અક્ષો અને અક્ષો સાથે સમાન ભીંગડા લંબચોરસ D ...

કાર્ટેસિન કોઓર્ડિનેટ્સબિગ એનસાયક્લોપેડિક પોલિટેકનિક ડિક્શનરી - (કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમ), પ્લેન પર અથવા અવકાશમાં એક સંકલન સિસ્ટમ, સામાન્ય રીતે પરસ્પર લંબચોરસ અક્ષો અને લંબચોરસ અક્ષો સાથે સમાન ભીંગડા સાથેનું નામ આર. ડેકાર્ટેસ...

કાર્ટેસિન કોઓર્ડિનેટ્સકુદરતી વિજ્ઞાન. જ્ઞાનકોશીય શબ્દકોશ - કાટખૂણો પર છેદતી બે અક્ષોના સંબંધમાં હાડકાં પર મળેલા કોઈપણ બિંદુને સ્થિત કરવા માટેની સિસ્ટમ. રેને ડેસકાર્ટેસ દ્વારા વિકસિત, આ સિસ્ટમનો આધાર બન્યો પ્રમાણભૂત પદ્ધતિઓગ્રાફિકલ રજૂઆત આડી રેખા… … શબ્દકોશમનોવિજ્ઞાન માં

કોઓર્ડિનેટ્સ- કોઓર્ડિનેટ્સ. પ્લેન પર (ડાબે) અને અવકાશમાં (જમણે). COORDINATES (લેટિન co એકસાથે અને ordinatus ક્રમાંકિતમાંથી), સંખ્યાઓ જે અવકાશમાં સીધી રેખા, સમતલ, સપાટી પરના બિંદુની સ્થિતિ નક્કી કરે છે. કોઓર્ડિનેટ્સ એ અંતર છે... સચિત્ર જ્ઞાનકોશીય શબ્દકોશ

સૂચનાઓ

લખો ગાણિતિક ક્રિયાઓલખાણ સ્વરૂપમાં અને પર શોધ ક્વેરી ફીલ્ડમાં દાખલ કરો હોમ પેજ Google સાઇટ જો તમે કેલ્ક્યુલેટરનો ઉપયોગ કરી શકતા નથી, પરંતુ ઇન્ટરનેટની ઍક્સેસ ધરાવો છો. આ સર્ચ એન્જિનમાં બિલ્ટ-ઇન મલ્ટિફંક્શનલ કેલ્ક્યુલેટર છે, જેનો ઉપયોગ અન્ય કોઈપણ કરતા વધુ સરળ છે. બટનો સાથે કોઈ ઇન્ટરફેસ નથી - તમામ ડેટા એક જ ક્ષેત્રમાં ટેક્સ્ટ સ્વરૂપમાં દાખલ કરવો આવશ્યક છે. ઉદાહરણ તરીકે, જો જાણીતું હોય સંકલન આત્યંતિક બિંદુઓ સેગમેન્ટત્રિ-પરિમાણીય સંકલન પ્રણાલી A(51.34 17.2 13.02) અને A(-11.82 7.46 33.5), પછી સંકલનમધ્યબિંદુ સેગમેન્ટ C((51.34-11.82)/2 (17.2+7.46)/2 (13.02+33.5)/2). શોધ ક્વેરી ફીલ્ડમાં (51.34-11.82)/2 દાખલ કરીને, પછી (17.2+7.46)/2 અને (13.02+33.5)/2, તમે મેળવવા માટે Google નો ઉપયોગ કરી શકો છો સંકલન C(19.76 12.33 23.26).

પ્રમાણભૂત સમીકરણવર્તુળ તમને ઘણા શોધવા માટે પરવાનગી આપે છે મહત્વપૂર્ણ માહિતીઆ આંકડો વિશે, ઉદાહરણ તરીકે, તેના કેન્દ્રના કોઓર્ડિનેટ્સ, ત્રિજ્યાની લંબાઈ. કેટલીક સમસ્યાઓમાં, તેનાથી વિપરીત, આપેલ પરિમાણોતમારે સમીકરણ બનાવવાની જરૂર છે.

સૂચનાઓ

તમને આપવામાં આવેલ કાર્યના આધારે વર્તુળ વિશે તમારી પાસે કઈ માહિતી છે તે નક્કી કરો. તે યાદ રાખો અંતિમ ધ્યેયકેન્દ્રના કોઓર્ડિનેટ્સ, તેમજ વ્યાસ નક્કી કરવાની જરૂર છે. તમારી બધી ક્રિયાઓ આ ચોક્કસ પરિણામ પ્રાપ્ત કરવાના લક્ષ્યમાં હોવી જોઈએ.

સંકલન રેખાઓ અથવા અન્ય રેખાઓ સાથે આંતરછેદના બિંદુઓની હાજરી પર ડેટાનો ઉપયોગ કરો. મહેરબાની કરીને નોંધ કરો કે જો વર્તુળ એબ્સીસા અક્ષમાંથી પસાર થાય છે, તો બીજામાં સંકલન 0 હશે, અને જો ઓર્ડિનેટ અક્ષમાંથી પસાર થશે, તો પ્રથમ. આ કોઓર્ડિનેટ્સ તમને વર્તુળના કેન્દ્રના કોઓર્ડિનેટ્સ શોધવા અને ત્રિજ્યાની ગણતરી કરવા દેશે.

સેકન્ટ્સ અને ટેન્જેન્ટ્સના મૂળભૂત ગુણધર્મો વિશે ભૂલશો નહીં. ખાસ કરીને, સૌથી ઉપયોગી પ્રમેય એ છે કે સંપર્કના બિંદુએ ત્રિજ્યા અને સ્પર્શક એક કાટખૂણો બનાવે છે. પરંતુ મહેરબાની કરીને નોંધ કરો કે તમને કોર્સ દરમિયાન ઉપયોગમાં લેવાતા તમામ પ્રમેયને સાબિત કરવા માટે કહેવામાં આવી શકે છે.

વર્તુળના સમીકરણ માટે ચોક્કસ ડેટાનો ઉપયોગ કેવી રીતે કરવો તે તરત જ જોવાનું શીખવા માટે સૌથી પ્રમાણભૂત પ્રકારો ઉકેલો. તેથી, સીધી સાથે પહેલાથી જ ઉલ્લેખિત કાર્યો ઉપરાંત આપેલ કોઓર્ડિનેટ્સઅને જેમાં આંતરછેદ બિંદુઓની હાજરી વિશેની માહિતી આપવામાં આવે છે, વર્તુળના સમીકરણનું સંકલન કરવા માટે, તમે વર્તુળના કેન્દ્ર, તારની લંબાઈ અને આ તાર જેના પર રહેલો છે તે વિશેના જ્ઞાનનો ઉપયોગ કરી શકો છો.

ઉકેલવા માટે, બાંધવું સમદ્વિબાજુ ત્રિકોણ, જેનો આધાર હશે આપેલ તાર, એ સમાન બાજુઓ– ત્રિજ્યા. કમ્પાઇલ કરો જેમાંથી તમે સરળતાથી જરૂરી ડેટા મેળવી શકો છો. આ કરવા માટે, પ્લેનમાં સેગમેન્ટની લંબાઈ શોધવા માટે સૂત્રનો ઉપયોગ કરવા માટે તે પૂરતું છે.

વિષય પર વિડિઓ

વર્તુળને એક આકૃતિ તરીકે સમજવામાં આવે છે જેમાં તેના કેન્દ્રથી સમાન અંતરે આવેલા પ્લેન પર ઘણા બધા બિંદુઓ હોય છે. કેન્દ્રથી બિંદુઓ સુધીનું અંતર વર્તુળત્રિજ્યા કહેવાય છે.

સામાન્ય મૂળ (કોઓર્ડિનેટ્સનું મૂળ) અને લંબાઈના સામાન્ય એકમ સાથે એકબીજાને લંબરૂપ બે અથવા ત્રણ છેદતી અક્ષોની ક્રમબદ્ધ સિસ્ટમ કહેવામાં આવે છે. લંબચોરસ કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમ .

સામાન્ય કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમ (affine કોઓર્ડિનેટ સિસ્ટમ)માં કાટખૂણે અક્ષો શામેલ હોઈ શકે નહીં. સન્માનમાં ફ્રેન્ચ ગણિતશાસ્ત્રીરેને ડેસકાર્ટેસ (1596-1662) એ આવી સંકલન પ્રણાલીનું નામ આપ્યું છે જેમાં લંબાઈનું એક સામાન્ય એકમ તમામ અક્ષો પર માપવામાં આવે છે અને અક્ષો સીધી હોય છે.

પ્લેન પર લંબચોરસ કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમ બે અક્ષો ધરાવે છે અને અવકાશમાં લંબચોરસ કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમ - ત્રણ અક્ષો. પ્લેન પર અથવા અવકાશમાં દરેક બિંદુ કોઓર્ડિનેટ્સના ક્રમબદ્ધ સમૂહ દ્વારા વ્યાખ્યાયિત કરવામાં આવે છે - સંકલન સિસ્ટમની લંબાઈના એકમને અનુરૂપ સંખ્યાઓ.

નોંધ કરો કે, વ્યાખ્યામાંથી નીચે મુજબ, એક સીધી રેખા પર, એટલે કે, એક પરિમાણમાં કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમ છે. લીટી પર કાર્ટેઝિયન કોઓર્ડિનેટ્સનો પરિચય એ એક એવી રીત છે કે જેના દ્વારા લીટી પરનો કોઈપણ બિંદુ સારી રીતે વ્યાખ્યાયિત વાસ્તવિક સંખ્યા સાથે સંકળાયેલ છે, એટલે કે, સંકલન.

રેને ડેસકાર્ટેસના કાર્યોમાં ઉદ્ભવેલી સંકલન પદ્ધતિએ તમામ ગણિતની ક્રાંતિકારી પુનઃરચના તરીકે ચિહ્નિત કર્યું. અર્થઘટન કરવું શક્ય બન્યું બીજગણિતીય સમીકરણો(અથવા અસમાનતા) ભૌમિતિક છબીઓ (ગ્રાફ) ના રૂપમાં અને તેનાથી વિપરીત, ઉકેલ માટે જુઓ ભૌમિતિક સમસ્યાઓવિશ્લેષણાત્મક સૂત્રો અને સમીકરણોની સિસ્ટમોનો ઉપયોગ કરીને. હા, અસમાનતા z < 3 геометрически означает полупространство, лежащее ниже плоскости, параллельной координатной плоскости xOyઅને 3 એકમો દ્વારા આ પ્લેન ઉપર સ્થિત છે.

કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમનો ઉપયોગ કરીને, આપેલ વળાંક પરના બિંદુનું સભ્યપદ એ હકીકતને અનુરૂપ છે કે સંખ્યાઓ xસમાન સ્કેલ અથવાકેટલાક સમીકરણને સંતોષો. આમ, આપેલ બિંદુ પર કેન્દ્ર સાથે વર્તુળ પરના બિંદુના કોઓર્ડિનેટ્સ ( a; b) સમીકરણને સંતોષો (x - a)² + ( અથવા - b)² = આર² .

પ્લેન પર લંબચોરસ કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમ

સમાન મૂળ અને સમાન સ્કેલ એકમ સ્વરૂપ સાથેના પ્લેન પર બે લંબરૂપ અક્ષો પ્લેન પર કાર્ટેશિયન લંબચોરસ કોઓર્ડિનેટ સિસ્ટમ . આમાંની એક ધરીને અક્ષ કહેવામાં આવે છે બળદ, અથવા x-અક્ષ , અન્ય - ધરી ઓય, અથવા y-અક્ષ . આ અક્ષોને સંકલન અક્ષો પણ કહેવામાં આવે છે. ચાલો દ્વારા સૂચિત કરીએ એમxઅને એમyઅનુક્રમે, એક મનસ્વી બિંદુનું પ્રક્ષેપણ એમધરી પર બળદઅને ઓય. અંદાજો કેવી રીતે મેળવવું? ચાલો બિંદુ મારફતે જાઓ એમ બળદ. આ સીધી રેખા ધરીને છેદે છે બળદબિંદુ પર એમx. ચાલો બિંદુ મારફતે જાઓ એમઅક્ષને લંબરૂપ સીધી રેખા ઓય. આ સીધી રેખા ધરીને છેદે છે ઓયબિંદુ પર એમy. આ નીચે ચિત્રમાં બતાવવામાં આવ્યું છે.

xઅને અથવાપોઈન્ટ એમઅમે તે મુજબ નિર્દેશિત સેગમેન્ટના મૂલ્યોને કૉલ કરીશું ઓમxઅને ઓમy. આ નિર્દેશિત સેગમેન્ટ્સના મૂલ્યોની ગણતરી તે મુજબ કરવામાં આવે છે x = x0 - 0 અને અથવા = અથવા0 - 0 . કાર્ટેશિયન કોઓર્ડિનેટ્સ xઅને અથવાપોઈન્ટ એમ એબ્સીસા સમાન સ્કેલ ઓર્ડિનેટ . હકીકત એ છે કે બિંદુ એમકોઓર્ડિનેટ્સ ધરાવે છે xઅને અથવા, નીચે પ્રમાણે સૂચવવામાં આવે છે: એમ(x, અથવા) .

સંકલન અક્ષો પ્લેનને ચાર ભાગમાં વહેંચે છે ચતુર્થાંશ , જેની સંખ્યા નીચેની આકૃતિમાં બતાવવામાં આવી છે. તે ચોક્કસ ચતુર્થાંશમાં તેમના સ્થાનના આધારે બિંદુઓના કોઓર્ડિનેટ્સ માટે સંકેતોની ગોઠવણ પણ દર્શાવે છે.

પ્લેન પર કાર્ટેસિયન લંબચોરસ કોઓર્ડિનેટ્સ ઉપરાંત, ધ્રુવીય સંકલન પ્રણાલીને પણ ઘણીવાર ગણવામાં આવે છે. એક કોઓર્ડિનેટ સિસ્ટમથી બીજામાં સંક્રમણની પદ્ધતિ વિશે - પાઠમાં ધ્રુવીય સંકલન પ્રણાલી .

અવકાશમાં લંબચોરસ કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમ

અવકાશમાં કાર્ટેશિયન કોઓર્ડિનેટ્સ પ્લેનમાં કાર્ટેશિયન કોઓર્ડિનેટ્સ સાથે સંપૂર્ણ સામ્યતામાં રજૂ કરવામાં આવે છે.

અવકાશમાં ત્રણ પરસ્પર લંબ અક્ષો ( સંકલન અક્ષો) સામાન્ય શરૂઆત સાથે ઓઅને તે જ સ્કેલ એકમ સાથે તેઓ રચે છે અવકાશમાં કાર્ટેશિયન લંબચોરસ સંકલન સિસ્ટમ .

આમાંથી એક ધરીને અક્ષ કહેવામાં આવે છે બળદ, અથવા x-અક્ષ , અન્ય - ધરી ઓય, અથવા y-અક્ષ , ત્રીજો - અક્ષ ઓઝ, અથવા ધરી લાગુ . દો એમx, એમy એમz- મનસ્વી બિંદુના અંદાજો એમધરી પર જગ્યા બળદ , ઓયઅને ઓઝઅનુક્રમે

ચાલો બિંદુ મારફતે જાઓ એમ બળદબળદબિંદુ પર એમx. ચાલો બિંદુ મારફતે જાઓ એમધરી પર લંબરૂપ વિમાન ઓય. આ વિમાન ધરીને છેદે છે ઓયબિંદુ પર એમy. ચાલો બિંદુ મારફતે જાઓ એમધરી પર લંબરૂપ વિમાન ઓઝ. આ વિમાન ધરીને છેદે છે ઓઝબિંદુ પર એમz.

કાર્ટેશિયન લંબચોરસ કોઓર્ડિનેટ્સ x , અથવાઅને zપોઈન્ટ એમઅમે તે મુજબ નિર્દેશિત સેગમેન્ટના મૂલ્યોને કૉલ કરીશું ઓમx, ઓમyસમાન સ્કેલ ઓમz. આ નિર્દેશિત સેગમેન્ટ્સના મૂલ્યોની ગણતરી તે મુજબ કરવામાં આવે છે x = x0 - 0 , અથવા = અથવા0 - 0 અને z = z0 - 0 .

કાર્ટેશિયન કોઓર્ડિનેટ્સ x , અથવાઅને zપોઈન્ટ એમતે મુજબ બોલાવવામાં આવે છે એબ્સીસા , ઓર્ડિનેટ સમાન સ્કેલ અરજી કરવી .

જોડીમાં લેવામાં આવેલા સંકલન અક્ષો સંકલન વિમાનોમાં સ્થિત છે xOy , yOzઅને zOx .

કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમમાં પોઈન્ટ વિશે સમસ્યાઓ

ઉદાહરણ 1.

વ્યાખ્યા 4. બિંદુ A નું એબ્સીસા એ બિંદુનું સંકલન છે(2; -3) ;

બી(3; -1) ;

સી(-5; 1) .

એબ્સીસા અક્ષ પર આ બિંદુઓના અંદાજોના કોઓર્ડિનેટ્સ શોધો.

ઉકેલ. આ પાઠના સૈદ્ધાંતિક ભાગમાંથી નીચે મુજબ, એબ્સીસા અક્ષ પર એક બિંદુનું પ્રક્ષેપણ એબ્સીસા અક્ષ પર જ સ્થિત છે, એટલે કે, અક્ષ બળદ, અને તેથી પોઈન્ટના એબ્સીસા સમાન એબ્સીસા ધરાવે છે, અને એક ઓર્ડિનેટ (અક્ષ પર સંકલન) ઓય, જેને x-અક્ષ બિંદુ 0 પર છેદે છે), શૂન્ય બરાબર. તેથી આપણે x-અક્ષ પર આ બિંદુઓના નીચેના કોઓર્ડિનેટ્સ મેળવીએ છીએ:

વ્યાખ્યા 4. બિંદુ A નું એબ્સીસા એ બિંદુનું સંકલન છેx(2;0);

બીx(3;0);

સીx (-5; 0).

ઉદાહરણ 2.કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમમાં, પ્લેન પર પોઈન્ટ આપવામાં આવે છે

વ્યાખ્યા 4. બિંદુ A નું એબ્સીસા એ બિંદુનું સંકલન છે(-3; 2) ;

બી(-5; 1) ;

સી(3; -2) .

ઓર્ડિનેટ અક્ષ પર આ બિંદુઓના અંદાજોના કોઓર્ડિનેટ્સ શોધો.

ઉકેલ. આ પાઠના સૈદ્ધાંતિક ભાગમાંથી નીચે મુજબ, ઓર્ડિનેટ અક્ષ પર બિંદુનું પ્રક્ષેપણ ઓર્ડિનેટ અક્ષ પર જ સ્થિત છે, એટલે કે, અક્ષ ઓય, અને તેથી તે પોઈન્ટના જ ઓર્ડિનેટ સમાન ઓર્ડિનેટ ધરાવે છે, અને એબ્સીસા (અક્ષ પર સંકલન) બળદ, જેને ઓર્ડિનેટ અક્ષ બિંદુ 0 પર છેદે છે), જે શૂન્યની બરાબર છે. તેથી આપણને ઓર્ડિનેટ અક્ષ પર આ બિંદુઓના નીચેના કોઓર્ડિનેટ્સ મળે છે:

વ્યાખ્યા 4. બિંદુ A નું એબ્સીસા એ બિંદુનું સંકલન છેy(0;2);

બીy(0;1);

સીy(0;-2).

ઉદાહરણ 3.કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમમાં, પ્લેન પર પોઈન્ટ આપવામાં આવે છે

વ્યાખ્યા 4. બિંદુ A નું એબ્સીસા એ બિંદુનું સંકલન છે(2; 3) ;

બી(-3; 2) ;

સી(-1; -1) .

બળદ .

બળદ બળદ બળદ, આપેલ પોઈન્ટ જેટલો જ એબ્સીસા અને એક ઓર્ડિનેટ સમાન હશે સંપૂર્ણ મૂલ્યઆપેલ બિંદુનું ઓર્ડિનેટ અને તેની વિરુદ્ધનું ચિહ્ન. તેથી આપણને અક્ષની સાપેક્ષમાં આ બિંદુઓ સાથે સપ્રમાણતા ધરાવતા બિંદુઓના નીચેના કોઓર્ડિનેટ્સ મળે છે બળદ :

એ"(2; -3) ;

બી"(-3; -2) ;

સી"(-1; 1) .

કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમનો ઉપયોગ કરીને સમસ્યાઓ જાતે ઉકેલો, અને પછી ઉકેલો જુઓ

ઉદાહરણ 4.નક્કી કરો કે કયા ચતુર્થાંશમાં (ક્વાર્ટર, ચતુર્થાંશ સાથે ચિત્રકામ - ફકરાના અંતે "પ્લેન પર લંબચોરસ કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમ") એક બિંદુ સ્થિત થઈ શકે છે એમ(x; અથવા) , જો

1) xy > 0 ;

2) xy < 0 ;

3) x − અથવા = 0 ;

4) x + અથવા = 0 ;

5) x + અથવા > 0 ;

6) x + અથવા < 0 ;

7) x − અથવા > 0 ;

8) x − અથવા < 0 .

ઉદાહરણ 5.કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમમાં, પ્લેન પર પોઈન્ટ આપવામાં આવે છે

વ્યાખ્યા 4. બિંદુ A નું એબ્સીસા એ બિંદુનું સંકલન છે(-2; 5) ;

બી(3; -5) ;

સી(a; b) .

અક્ષની તુલનામાં આ બિંદુઓના સપ્રમાણતાવાળા બિંદુઓના કોઓર્ડિનેટ્સ શોધો ઓય .

ચાલો સાથે મળીને સમસ્યાઓ હલ કરવાનું ચાલુ રાખીએ

ઉદાહરણ 6.કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમમાં, પ્લેન પર પોઈન્ટ આપવામાં આવે છે

વ્યાખ્યા 4. બિંદુ A નું એબ્સીસા એ બિંદુનું સંકલન છે(-1; 2) ;

બી(3; -1) ;

સી(-2; -2) .

અક્ષની તુલનામાં આ બિંદુઓના સપ્રમાણતાવાળા બિંદુઓના કોઓર્ડિનેટ્સ શોધો ઓય .

ઉકેલ. ધરીની આસપાસ 180 ડિગ્રી ફેરવો ઓયઅક્ષમાંથી દિશાત્મક સેગમેન્ટ ઓયઆ બિંદુ સુધી. આકૃતિમાં, જ્યાં પ્લેનના ચતુર્થાંશ દર્શાવવામાં આવ્યા છે, ત્યાં આપણે જોઈએ છીએ કે અક્ષની તુલનામાં આપેલ એક સાથે સપ્રમાણતા ધરાવે છે. ઓય, આપેલ બિંદુ જેટલો જ ઓર્ડિનેટ ધરાવશે અને આપેલ બિંદુના એબ્સીસાના નિરપેક્ષ મૂલ્યમાં સમાન અને ચિહ્નમાં વિરુદ્ધ એબ્સીસા હશે. તેથી આપણને અક્ષની સાપેક્ષમાં આ બિંદુઓ સાથે સપ્રમાણતા ધરાવતા બિંદુઓના નીચેના કોઓર્ડિનેટ્સ મળે છે ઓય :

એ"(1; 2) ;

બી"(-3; -1) ;

સી"(2; -2) .

ઉદાહરણ 7.કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમમાં, પ્લેન પર પોઈન્ટ આપવામાં આવે છે

વ્યાખ્યા 4. બિંદુ A નું એબ્સીસા એ બિંદુનું સંકલન છે(3; 3) ;

બી(2; -4) ;

સી(-2; 1) .

ઉત્પત્તિના સંબંધમાં આ બિંદુઓના સપ્રમાણતાવાળા બિંદુઓના કોઓર્ડિનેટ્સ શોધો.

ઉકેલ. અમે મૂળથી આપેલ બિંદુ સુધી જતા નિર્દેશિત સેગમેન્ટને મૂળની આસપાસ 180 ડિગ્રી ફેરવીએ છીએ. આકૃતિમાં, જ્યાં સમતલના ચતુર્થાંશ દર્શાવેલ છે, આપણે જોઈએ છીએ કે કોઓર્ડિનેટ્સની ઉત્પત્તિના સંબંધમાં આપેલ બિંદુની સપ્રમાણતા ધરાવતા બિંદુમાં એબ્સીસા હશે અને આપેલ બિંદુના એબ્સીસા અને ઓર્ડિનેટના નિરપેક્ષ મૂલ્યમાં સમાન હશે, પરંતુ ચિહ્નમાં વિરુદ્ધ. તેથી આપણે મૂળની તુલનામાં આ બિંદુઓ સાથે સપ્રમાણતા ધરાવતા બિંદુઓના નીચેના કોઓર્ડિનેટ્સ મેળવીએ છીએ:

એ"(-3; -3) ;

બી"(-2; 4) ;

સી(2; -1) .

ઉદાહરણ 8.

વ્યાખ્યા 4. બિંદુ A નું એબ્સીસા એ બિંદુનું સંકલન છે(4; 3; 5) ;

બી(-3; 2; 1) ;

સી(2; -3; 0) .

આ બિંદુઓના અંદાજોના કોઓર્ડિનેટ્સ શોધો:

1) પ્લેનમાં ઓક્સી ;

2) પ્લેનમાં ઓક્સઝ ;

3) પ્લેનમાં ઓયઝ ;

4) એબ્સીસા અક્ષ પર;

5) ઓર્ડિનેટ અક્ષ પર;

6) એપ્લિકેશન અક્ષ પર.

1) પ્લેન પર બિંદુનું પ્રક્ષેપણ ઓક્સીઆ પ્લેન પર જ સ્થિત છે, અને તેથી આપેલ બિંદુના એબ્સીસા અને ઓર્ડિનેટ સમાન એબ્સીસા અને ઓર્ડિનેટ અને શૂન્યની બરાબર એપ્લીકેશન ધરાવે છે. તેથી આપણે આ બિંદુઓના અંદાજોના નીચેના કોઓર્ડિનેટ્સ મેળવીએ છીએ ઓક્સી :

વ્યાખ્યા 4. બિંદુ A નું એબ્સીસા એ બિંદુનું સંકલન છેxy (4; 3; 0);

બીxy (-3; 2; 0);

સીxy(2;-3;0).

2) પ્લેન પર બિંદુનું પ્રક્ષેપણ ઓક્સઝઆ પ્લેન પર જ સ્થિત છે, અને તેથી આપેલ બિંદુના એબ્સીસા અને એપ્લીકેટ સમાન એબ્સીસા અને એપ્લીકેટ છે, અને શૂન્યની બરાબર ઓર્ડિનેટ છે. તેથી આપણને આ બિંદુઓના અંદાજોના નીચેના કોઓર્ડિનેટ્સ મળે છે ઓક્સઝ :

વ્યાખ્યા 4. બિંદુ A નું એબ્સીસા એ બિંદુનું સંકલન છેxz (4; 0; 5);

બીxz (-3; 0; 1);

સીxz (2; 0; 0).

3) પ્લેન પર બિંદુનું પ્રક્ષેપણ ઓયઝઆ પ્લેન પર જ સ્થિત છે, અને તેથી આપેલ બિંદુના ઓર્ડિનેટ અને એપ્લીકેટ સમાન ઓર્ડિનેટ અને એપ્લીકેટ છે અને શૂન્યની બરાબર એબ્સીસા છે. તેથી આપણે આ બિંદુઓના અંદાજોના નીચેના કોઓર્ડિનેટ્સ મેળવીએ છીએ ઓયઝ :

વ્યાખ્યા 4. બિંદુ A નું એબ્સીસા એ બિંદુનું સંકલન છેyz(0; 3; 5);

બીyz (0; 2; 1);

સીyz (0; -3; 0).

4) આ પાઠના સૈદ્ધાંતિક ભાગમાંથી નીચે મુજબ, એબ્સીસા અક્ષ પરના બિંદુનું પ્રક્ષેપણ એબ્સીસા અક્ષ પર જ સ્થિત છે, એટલે કે, ધરી બળદ, અને તેથી પોઈન્ટના એબ્સીસા સમાન એબ્સીસા ધરાવે છે, અને પ્રક્ષેપણના ઓર્ડિનેટ અને એપ્લીકેટ શૂન્યના બરાબર છે (કારણ કે ઓર્ડિનેટ અને એપ્લીકેટ અક્ષ એબ્સીસાને પોઈન્ટ 0 પર છેદે છે). અમે એબ્સીસા અક્ષ પર આ બિંદુઓના અંદાજોના નીચેના કોઓર્ડિનેટ્સ મેળવીએ છીએ:

વ્યાખ્યા 4. બિંદુ A નું એબ્સીસા એ બિંદુનું સંકલન છેx(4;0;0);

બીx (-3; 0; 0);

સીx(2;0;0).

5) ઓર્ડિનેટ અક્ષ પર બિંદુનું પ્રક્ષેપણ ઓર્ડિનેટ અક્ષ પર જ સ્થિત છે, એટલે કે, અક્ષ ઓય, અને તેથી તે પોઈન્ટના જ ઓર્ડિનેટ સમાન ઓર્ડિનેટ ધરાવે છે, અને પ્રક્ષેપણના એબ્સીસા અને એપ્લીકેટ શૂન્ય સમાન છે (કારણ કે એબ્સીસા અને એપ્લીકેટ અક્ષ બિંદુ 0 પર ઓર્ડિનેટ અક્ષને છેદે છે). અમે ઓર્ડિનેટ અક્ષ પર આ બિંદુઓના અંદાજોના નીચેના કોઓર્ડિનેટ્સ મેળવીએ છીએ:

વ્યાખ્યા 4. બિંદુ A નું એબ્સીસા એ બિંદુનું સંકલન છેy(0; 3; 0);

બીy (0; 2; 0);

સીy(0;-3;0).

6) એપ્લીકેટ અક્ષ પરના બિંદુનું પ્રક્ષેપણ એપ્લીકેટ અક્ષ પર જ સ્થિત છે, એટલે કે, ધરી ઓઝ, અને તેથી પોઈન્ટના જ એપ્લીકેટ સમાન એપ્લીકેટ ધરાવે છે, અને પ્રક્ષેપણના એબ્સીસા અને ઓર્ડિનેટ શૂન્યની બરાબર છે (કારણ કે એબ્સીસા અને ઓર્ડિનેટ અક્ષ એપ્લીકેટ અક્ષને બિંદુ 0 પર છેદે છે). અમે એપ્લિકેશન અક્ષ પર આ બિંદુઓના અંદાજોના નીચેના કોઓર્ડિનેટ્સ મેળવીએ છીએ:

વ્યાખ્યા 4. બિંદુ A નું એબ્સીસા એ બિંદુનું સંકલન છેz (0; 0; 5);

બીz (0; 0; 1);

સીz(0; 0; 0).

ઉદાહરણ 9.કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમમાં, જગ્યામાં પોઈન્ટ આપવામાં આવે છે

વ્યાખ્યા 4. બિંદુ A નું એબ્સીસા એ બિંદુનું સંકલન છે(2; 3; 1) ;

બી(5; -3; 2) ;

સી(-3; 2; -1) .

આ બિંદુઓના સંદર્ભમાં સપ્રમાણતાવાળા બિંદુઓના કોઓર્ડિનેટ્સ શોધો:

1) વિમાન ઓક્સી ;

2) વિમાનો ઓક્સઝ ;

3) વિમાનો ઓયઝ ;

4) એબ્સીસા અક્ષો;

5) અક્ષો ગોઠવો;

6) અક્ષો લાગુ કરો;

7) કોઓર્ડિનેટ્સનું મૂળ.

1) ધરીની બીજી બાજુના બિંદુને “ખસેડો” ઓક્સી ઓક્સી, આપેલ પોઈન્ટના એબ્સીસા અને ઓર્ડિનેટની સમાન એબ્સીસા અને ઓર્ડિનેટ હશે, અને આપેલ બિંદુના અનુરૂપની તીવ્રતામાં સમાન એપ્લિકેશન, પરંતુ ચિહ્નમાં વિરુદ્ધ હશે. તેથી, અમને પ્લેન સંબંધિત ડેટાના સપ્રમાણતાવાળા બિંદુઓના નીચેના કોઓર્ડિનેટ્સ મળે છે ઓક્સી :

એ"(2; 3; -1) ;

બી"(5; -3; -2) ;

સી"(-3; 2; 1) .

2) ધરીની બીજી બાજુના બિંદુને “ખસેડો” ઓક્સઝસમાન અંતર સુધી. કોઓર્ડિનેટ સ્પેસ દર્શાવતી આકૃતિમાંથી, આપણે જોઈએ છીએ કે ધરીની સાપેક્ષમાં આપેલ એક બિંદુ સાથે સપ્રમાણતા ધરાવે છે. ઓક્સઝ, આપેલ પોઈન્ટના એબ્સીસા અને એપ્લીકેટની બરાબર એબ્સીસા અને એપ્લીકેટ હશે, અને આપેલ પોઈન્ટના ઓર્ડિનેટની તીવ્રતામાં સમાન ઓર્ડિનેટ હશે, પરંતુ ચિહ્નમાં વિરુદ્ધ હશે. તેથી, અમને પ્લેન સંબંધિત ડેટાના સપ્રમાણતાવાળા બિંદુઓના નીચેના કોઓર્ડિનેટ્સ મળે છે ઓક્સઝ :

એ"(2; -3; 1) ;

બી"(5; 3; 2) ;

સી"(-3; -2; -1) .

3) ધરીની બીજી બાજુના બિંદુને “ખસેડો” ઓયઝસમાન અંતર સુધી. કોઓર્ડિનેટ સ્પેસ દર્શાવતી આકૃતિમાંથી, આપણે જોઈએ છીએ કે ધરીની સાપેક્ષમાં આપેલ એક બિંદુ સાથે સપ્રમાણતા ધરાવે છે. ઓયઝ, આપેલ પોઈન્ટના ઓર્ડિનેટ અને એપ્લીકેટની સમાન ઓર્ડિનેટ અને એપ્લીકેટ હશે, અને આપેલ બિંદુના એબ્સીસાના મૂલ્યમાં સમાન એબ્સીસા હશે, પરંતુ ચિહ્નમાં વિરુદ્ધ હશે. તેથી, અમને પ્લેન સંબંધિત ડેટાના સપ્રમાણતાવાળા બિંદુઓના નીચેના કોઓર્ડિનેટ્સ મળે છે ઓયઝ :

એ"(-2; 3; 1) ;

બી"(-5; -3; 2) ;

સી"(3; 2; -1) .

સાથે સામ્યતા દ્વારા સપ્રમાણ બિંદુઓપ્લેન પર અને અવકાશમાંના બિંદુઓ વિમાનોને સંબંધિત ડેટાની સમપ્રમાણતા ધરાવે છે, અમે નોંધીએ છીએ કે અવકાશમાં કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમના કેટલાક અક્ષના સંદર્ભમાં સમપ્રમાણતાના કિસ્સામાં, અક્ષ પરના સંકલન જે સંદર્ભમાં સમપ્રમાણતા આપવામાં આવે છે. તેની નિશાની જાળવી રાખશે, અને અન્ય બે અક્ષો પરના કોઓર્ડિનેટ્સ ચોક્કસ દ્રષ્ટિએ આપેલ બિંદુના કોઓર્ડિનેટ્સ જેટલું જ મૂલ્ય સમાન હશે, પરંતુ ચિહ્નમાં વિરુદ્ધ હશે.

4) એબ્સીસા તેની નિશાની જાળવી રાખશે, પરંતુ ઓર્ડિનેટ અને લાગુ ચિહ્નો બદલશે. તેથી, અમે એબ્સીસા અક્ષને લગતા ડેટાના સપ્રમાણતાવાળા બિંદુઓના નીચેના કોઓર્ડિનેટ્સ મેળવીએ છીએ:

એ"(2; -3; -1) ;

બી"(5; 3; -2) ;

સી"(-3; -2; 1) .

5) ઓર્ડિનેટ તેની નિશાની જાળવી રાખશે, પરંતુ એબ્સીસા અને એપ્લીકેટ ચિહ્નો બદલશે. તેથી, અમે ઓર્ડિનેટ અક્ષને સંબંધિત ડેટાના સપ્રમાણતાવાળા બિંદુઓના નીચેના કોઓર્ડિનેટ્સ મેળવીએ છીએ:

એ"(-2; 3; -1) ;

બી"(-5; -3; -2) ;

સી"(3; 2; 1) .

6) અરજીકર્તા તેની નિશાની જાળવી રાખશે, પરંતુ એબ્સીસા અને ઓર્ડિનેટ ચિહ્નો બદલશે. તેથી, અમે એપ્લિકેશન અક્ષને સંબંધિત ડેટાના સપ્રમાણતાવાળા બિંદુઓના નીચેના કોઓર્ડિનેટ્સ મેળવીએ છીએ:

એ"(-2; -3; 1) ;

બી"(-5; 3; 2) ;

સી"(3; -2; -1) .

7) સમતલ પરના બિંદુઓના કિસ્સામાં સમપ્રમાણતા સાથે સામ્યતા દ્વારા, કોઓર્ડિનેટ્સની ઉત્પત્તિ વિશે સપ્રમાણતાના કિસ્સામાં, આપેલ બિંદુના સપ્રમાણતાવાળા બિંદુના તમામ કોઓર્ડિનેટ્સ આપેલ બિંદુના કોઓર્ડિનેટ્સના ચોક્કસ મૂલ્યમાં સમાન હશે, પરંતુ ચિહ્નમાં વિરુદ્ધ. તેથી, અમે મૂળના સંબંધમાં ડેટાને સપ્રમાણતા ધરાવતા બિંદુઓના નીચેના કોઓર્ડિનેટ્સ મેળવીએ છીએ.

ધ્રુવીય કોઓર્ડિનેટ્સ

નંબર પર બોલાવવામાં આવે છે ધ્રુવીય ત્રિજ્યાબિંદુઓ અથવા પ્રથમ ધ્રુવીય સંકલન. અંતર નકારાત્મક હોઈ શકતું નથી, તેથી કોઈપણ બિંદુની ધ્રુવીય ત્રિજ્યા છે. પ્રથમ ધ્રુવીય સંકલન પણ સૂચવવામાં આવે છે ગ્રીક અક્ષર(“ro”), પરંતુ હું લેટિન વર્ઝનનો ઉપયોગ કરું છું અને ભવિષ્યમાં તેનો ઉપયોગ કરીશ.

નંબર પર બોલાવવામાં આવે છે ધ્રુવીય કોણઆપેલ બિંદુ અથવા બીજું ધ્રુવીય સંકલન. ધ્રુવીય કોણ સામાન્ય રીતે અંદર બદલાય છે (કહેવાતા મુખ્ય કોણ મૂલ્યો). જો કે, શ્રેણીનો ઉપયોગ કરવો તે તદ્દન સ્વીકાર્ય છે, અને કેટલાક કિસ્સાઓમાં શૂન્યથી "વત્તા અનંત" સુધીના તમામ ખૂણા મૂલ્યોને ધ્યાનમાં લેવાની સીધી જરૂર છે. માર્ગ દ્વારા, હું ભલામણ કરું છું કે તમે કોણના રેડિયન માપની આદત પાડો, કારણ કે તમે ડિગ્રી સાથે કામ કરો છો ઉચ્ચ ગણિતનથી માનવામાં આવે છે.

યુગલ કહેવાય છે ધ્રુવીય કોઓર્ડિનેટ્સબિંદુઓ તેઓ શોધવા માટે સરળ છે અને ચોક્કસ મૂલ્યો. સ્પર્શક તીવ્ર કોણજમણો ત્રિકોણ - બાજુની બાજુની વિરુદ્ધ બાજુનો ગુણોત્તર છે: તેથી, કોણ પોતે: . પાયથાગોરિયન પ્રમેય મુજબ, કર્ણનો વર્ગ સરવાળો સમાનપગના ચોરસ: તેથી, ધ્રુવીય ત્રિજ્યા:

આમ, .

એક પેંગ્વિન સારું છે, પરંતુ ટોળું સારું છે:


નકારાત્મક લક્ષી કોણ મેં તેને તીર વડે ચિહ્નિત કર્યું છે, જો કેટલાક વાચકો હજુ સુધી આ અભિગમ વિશે જાણતા ન હોય. જો ઇચ્છિત હોય, તો તમે દરેકને 1 વળાંક (રેડ. અથવા 360 ડિગ્રી) "સ્ક્રૂ" કરી શકો છો અને, માર્ગ દ્વારા, આરામદાયક મેળવી શકો છો કોષ્ટક મૂલ્યો:

પરંતુ આ "પરંપરાગત" લક્ષી ખૂણાઓનો ગેરલાભ એ છે કે તે ઘડિયાળની વિરુદ્ધ દિશામાં ખૂબ દૂર (180 ડિગ્રીથી વધુ) "ટ્વિસ્ટેડ" છે. હું પ્રશ્નની અપેક્ષા રાખું છું: “શા માટે અછત છે અને શા માટે છે નકારાત્મક ખૂણા? ગણિતમાં, સૌથી ટૂંકી અને તર્કસંગત રીતો. ઠીક છે, ભૌતિકશાસ્ત્રના દૃષ્ટિકોણથી, પરિભ્રમણની દિશા ઘણીવાર મૂળભૂત મહત્વની હોય છે - આપણામાંના દરેકએ હેન્ડલને ખોટી દિશામાં ખેંચીને દરવાજો ખોલવાનો પ્રયાસ કર્યો =)

ધ્રુવીય કોઓર્ડિનેટ્સમાં પોઈન્ટ બનાવવાનો ક્રમ અને તકનીક

સુંદર ચિત્રોસુંદર, પરંતુ બિલ્ટ ઇન ધ્રુવીય સિસ્ટમકોઓર્ડિનેટ્સ એ એક જગ્યાએ ઉદ્યમી કાર્ય છે. ધ્રુવીય ખૂણો હોય તેવા બિંદુઓમાં કોઈ મુશ્કેલી નથી , અમારા ઉદાહરણમાં આ બિંદુઓ છે ; મૂલ્યો કે જે 45 ડિગ્રીના ગુણાંકમાં છે તે પણ વધુ મુશ્કેલીનું કારણ નથી: . પરંતુ કેવી રીતે યોગ્ય રીતે અને નિપુણતાથી બાંધવું, કહો, એક બિંદુ?

તમારે કાગળનો ચેકર્ડ ટુકડો, પેન્સિલ અને નીચેનાની જરૂર પડશે ચિત્રકામ સાધનો: શાસક, હોકાયંત્ર, પ્રોટ્રેક્ટર. IN છેલ્લા ઉપાય તરીકે, તમે માત્ર એક જ શાસક સાથે મેળવી શકો છો, અથવા તો... તેના વિના બિલકુલ! આગળ વાંચો અને તમને બીજો પુરાવો મળશે કે આ દેશ અજેય છે =)

ઉદાહરણ 1

ધ્રુવીય સંકલન પ્રણાલીમાં એક બિંદુ બનાવો.

સૌ પ્રથમ, તમારે શોધવાની જરૂર છે ડિગ્રી માપકોણ જો ખૂણો અજાણ્યો છે અથવા તમને શંકા છે, તો તેનો ઉપયોગ કરવો હંમેશા વધુ સારું છે ટેબલઅથવા રેડિયનને ડિગ્રીમાં કન્વર્ટ કરવા માટેનું સામાન્ય સૂત્ર. તો આપણો કોણ (અથવા) છે.

ચાલો ધ્રુવીય સંકલન પ્રણાલી દોરીએ (પાઠની શરૂઆત જુઓ) અને પ્રોટ્રેક્ટર પસંદ કરીએ. રાઉન્ડ ઇન્સ્ટ્રુમેન્ટના માલિકોને 240 ડિગ્રી ચિહ્નિત કરવામાં કોઈ મુશ્કેલી પડશે નહીં, પરંતુ સાથે ઉચ્ચ સંભાવનાતમારા હાથમાં ઉપકરણનું અર્ધવર્તુળાકાર સંસ્કરણ હશે. સમસ્યા સંપૂર્ણ ગેરહાજરીજો તમારી પાસે પ્રિન્ટર અને કાતર હોય તો પ્રોટ્રેક્ટર હસ્તકલા દ્વારા ઉકેલવામાં આવે છે.

ત્યાં બે રીત છે: શીટને ફેરવો અને 120 ડિગ્રીને ચિહ્નિત કરો, અથવા અડધા વળાંકને "સ્ક્રૂ કરો" અને તપાસો વિરુદ્ધ ખૂણો. ચાલો પુખ્ત પદ્ધતિ પસંદ કરીએ અને 60 ડિગ્રીનું ચિહ્ન બનાવીએ:


કાં તો લિલિપ્યુટિયન પ્રોટ્રેક્ટર, અથવા વિશાળ પાંજરું =) જો કે, કોણ માપવા માટે, સ્કેલ મહત્વપૂર્ણ નથી.

પેન્સિલનો ઉપયોગ કરીને, ધ્રુવમાંથી પસાર થતી પાતળી સીધી રેખા દોરો અને બનાવેલ ચિહ્ન:


અમે ખૂણો ગોઠવ્યો છે, હવે ધ્રુવીય ત્રિજ્યા આગળ છે. હોકાયંત્ર લો અને રેખા સાથેઅમે તેનું સોલ્યુશન 3 એકમો પર સેટ કર્યું છે, મોટેભાગે આ, અલબત્ત, સેન્ટિમીટર છે:

હવે કાળજીપૂર્વક સોયને ધ્રુવ પર મૂકો, અને રોટેશનલ ચળવળઅમે એક નાનો સેરિફ (લાલ રંગ) બનાવીએ છીએ. જરૂરી બિંદુ બનાવવામાં આવ્યું હતું:


તમે સીધી બાંધેલી સીધી રેખા પર શાસક લાગુ કરીને અને 3 સેન્ટિમીટર માપીને હોકાયંત્ર વિના કરી શકો છો. પરંતુ, જેમ આપણે પછી જોઈશું, ધ્રુવીય સંકલન પ્રણાલીમાં બાંધકામને લગતી સમસ્યાઓમાંસામાન્ય પરિસ્થિતિ એ છે જ્યારે તમારે બે અથવા ચિહ્નિત કરવાની જરૂર હોય વધુસમાન ધ્રુવીય ત્રિજ્યા સાથે નિર્દેશ કરે છે, તેથી તે મેટલને સખત કરવા માટે વધુ કાર્યક્ષમ છે. ખાસ કરીને, અમારા ડ્રોઇંગમાં, હોકાયંત્રના પગને 180 ડિગ્રી ફેરવવાથી, ધ્રુવની સાપેક્ષે એક બિંદુ સપ્રમાણ બનાવવું અને બીજી નોચ બનાવવી સરળ છે. ચાલો તેનો ઉપયોગ આગલા ફકરામાં સામગ્રી દ્વારા કામ કરવા માટે કરીએ:

લંબચોરસ અને ધ્રુવીય સંકલન પ્રણાલીઓ વચ્ચેનો સંબંધ

દેખીતી રીતે ચાલો ઉમેરીએધ્રુવીય સંકલન પ્રણાલીમાં, "નિયમિત" સંકલન ગ્રીડ અને ચિત્રમાં એક બિંદુ દોરો:

ધ્રુવીય કોઓર્ડિનેટ્સ દોરતી વખતે આ જોડાણને ધ્યાનમાં રાખવું હંમેશા ઉપયોગી છે. તેમ છતાં, વિલી-નિલી, તે કોઈ વધુ સંકેત વિના પોતાને સૂચવે છે.

ચાલો ઉદાહરણનો ઉપયોગ કરીને ધ્રુવીય અને કાર્ટેશિયન કોઓર્ડિનેટ્સ વચ્ચેનો સંબંધ સ્થાપિત કરીએ ચોક્કસ બિંદુ. ચાલો વિચાર કરીએ જમણો ત્રિકોણ, જેમાં કર્ણ ધ્રુવીય ત્રિજ્યા સમાન છે: , અને પગ કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમમાં બિંદુના "X" અને "Y" કોઓર્ડિનેટ્સ સમાન છે: .

એક્યુટ એંગલની સાઈન એ કર્ણની વિરુદ્ધ બાજુનો ગુણોત્તર છે:

તીવ્ર કોણનો કોસાઇન એ ગુણોત્તર છે અડીને પગકર્ણ માટે:

તે જ સમયે, અમે સર્વગ્રાહી શાળાના 9મા ધોરણના અભ્યાસક્રમમાંથી સાઈન, કોસાઈન (અને થોડી અગાઉની સ્પર્શક) ની વ્યાખ્યાઓનું પુનરાવર્તન કર્યું.

કૃપા કરીને તમારી સંદર્ભ પુસ્તકમાં કાર્યકારી સૂત્રો ઉમેરો જે કોઈ બિંદુના કાર્ટેશિયન કોઓર્ડિનેટ્સ તેના ધ્રુવીય કોઓર્ડિનેટ્સ દ્વારા વ્યક્ત કરે છે - અમારે તેમની સાથે એક કરતા વધુ વાર વ્યવહાર કરવો પડશે, અને હવે પછીની વખતે =)

ચાલો બિંદુના કોઓર્ડિનેટ્સ શોધીએ લંબચોરસ સિસ્ટમસંકલન:

આમ:

પરિણામી સૂત્રો બાંધકામની સમસ્યામાં બીજી છટકબારી ખોલે છે, જ્યારે તમે પ્રોટ્રેક્ટર વિના બિલકુલ કરી શકો છો: પહેલા આપણે બિંદુના કાર્ટેશિયન કોઓર્ડિનેટ્સ શોધીએ છીએ (અલબત્ત, ડ્રાફ્ટમાં), પછી આપણે માનસિક રીતે ડ્રોઇંગ પર ઇચ્છિત સ્થાન શોધીએ છીએ. અને ચિહ્નિત કરો આ બિંદુ. ચાલુ અંતિમ તબક્કોએક પાતળી સીધી રેખા દોરો જે બાંધેલા બિંદુ અને ધ્રુવમાંથી પસાર થાય છે. પરિણામે, તે તારણ આપે છે કે કોણ કથિત રીતે પ્રોટ્રેક્ટર સાથે માપવામાં આવ્યું હતું.

તે રમુજી છે કે ખૂબ જ ભયાવહ વિદ્યાર્થીઓ શાસક વિના પણ કરી શકે છે, તેના બદલે પાઠ્યપુસ્તક, નોટબુક અથવા તેની સરળ ધારનો ઉપયોગ કરીને ગ્રેડ પુસ્તક- છેવટે, નોટબુક ઉત્પાદકોએ મેટ્રિક્સની કાળજી લીધી, 1 સેલ = 5 મિલીમીટર.

આ બધું મને એક જાણીતી મજાકની યાદ અપાવે છે જેમાં કોઠાસૂઝ ધરાવનાર પાઇલોટ્સે બેલોમોરના પેક સાથે કોર્સ રચ્યો હતો =) જો કે, ટુચકાઓ એક બાજુએ, મજાક વાસ્તવિકતાથી દૂર નથી, મને યાદ છે કે રશિયનમાં સ્થાનિક ફ્લાઇટ્સમાંથી એક પર ફેડરેશન, એરલાઇનરમાં તમામ નેવિગેશન સાધનો નિષ્ફળ ગયા, અને ક્રૂએ નિયમિત ગ્લાસ પાણીનો ઉપયોગ કરીને પ્લેનને સફળતાપૂર્વક લેન્ડ કર્યું, જે જમીનની સાપેક્ષ પ્લેનનો કોણ દર્શાવે છે. અને એરસ્ટ્રીપ - તે અહીં છે, વિન્ડશિલ્ડમાંથી દૃશ્યમાન છે.

પાઠની શરૂઆતમાં ટાંકવામાં આવેલ પાયથાગોરિયન પ્રમેયનો ઉપયોગ કરીને, તે મેળવવાનું સરળ છે વ્યસ્ત સૂત્રો: , તેથી:

ખૂણો "ફી" પોતે પ્રમાણભૂત રીતે આર્કટેન્જેન્ટ દ્વારા વ્યક્ત થાય છે - બિલકુલ સમાન જટિલ સંખ્યાની દલીલતેની બધી મુશ્કેલીઓ સાથે.

તમારા સંદર્ભ સામાનમાં સૂત્રોના બીજા જૂથને મૂકવાની પણ સલાહ આપવામાં આવે છે.

પછી વિગતવાર વિશ્લેષણવ્યક્તિગત મુદ્દાઓ સાથે ફ્લાઇટ્સ, ચાલો વિષયના કુદરતી ચાલુ પર આગળ વધીએ:

ધ્રુવીય કોઓર્ડિનેટ્સમાં રેખાનું સમીકરણ

આવશ્યકપણે, ધ્રુવીય સંકલન પ્રણાલીમાં રેખાનું સમીકરણ છે ધ્રુવીય કોણમાંથી ધ્રુવીય ત્રિજ્યાનું કાર્ય (દલીલ). આ કિસ્સામાં, ધ્રુવીય કોણ ધ્યાનમાં લેવામાં આવે છે રેડિયનમાં(!) અને સતતથી મૂલ્યો લે છે (ક્યારેક તેને અનંત માનવામાં આવવું જોઈએ, અથવા થી સુધીની સુવિધા માટે ઘણી સમસ્યાઓમાં). કોણ “phi” નું દરેક મૂલ્ય જેમાં શામેલ છે વ્યાખ્યાનું ક્ષેત્રકાર્ય, ધ્રુવીય ત્રિજ્યાના એક મૂલ્યને અનુલક્ષે છે.

ધ્રુવીય કાર્યની તુલના એક પ્રકારના રડાર સાથે કરી શકાય છે - જ્યારે ધ્રુવમાંથી નીકળતો પ્રકાશનો કિરણ ઘડિયાળની વિરુદ્ધ દિશામાં ફરે છે અને એક રેખા "શોધે છે" (ખેંચે છે).

ધ્રુવીય વળાંકનું પ્રમાણભૂત ઉદાહરણ છે આર્કિમીડિયન સર્પાકાર. નીચેનું ચિત્ર તેણીને બતાવે છે પ્રથમ રાઉન્ડ- જ્યારે ધ્રુવીય ખૂણાને અનુસરતા ધ્રુવીય ત્રિજ્યા 0 થી મૂલ્યો લે છે:

આગળ, બિંદુ પર ધ્રુવીય ધરીને પાર કરીને, સર્પાકાર ધ્રુવથી અનંત દૂર ખસીને, આરામ કરવાનું ચાલુ રાખશે. પણ સમાન કેસોવ્યવહારમાં તેઓ તદ્દન દુર્લભ છે; વધુ લાક્ષણિક પરિસ્થિતિ, જ્યારે અનુગામી ક્રાંતિ વખતે આપણે "એ જ લાઇન સાથે ચાલીએ છીએ" જે શ્રેણીમાં પ્રાપ્ત થઈ હતી.

પ્રથમ ઉદાહરણમાં આપણે ખ્યાલ પર આવીએ છીએ વ્યાખ્યાનું ક્ષેત્રધ્રુવીય કાર્ય: ધ્રુવીય ત્રિજ્યા બિન-ઋણાત્મક હોવાથી, નકારાત્મક ખૂણાઓને અહીં ગણી શકાય નહીં.

! નોંધ : કેટલાક કિસ્સાઓમાં તેનો ઉપયોગ કરવાનો રિવાજ છે સામાન્યકૃત ધ્રુવીય કોઓર્ડિનેટ્સ, જ્યાં ત્રિજ્યા નકારાત્મક હોઈ શકે છે, અને અમે થોડા સમય પછી આ અભિગમનો ટૂંકમાં અભ્યાસ કરીશું

આર્કિમિડીઝ સર્પાકાર ઉપરાંત, અન્ય ઘણા પ્રખ્યાત વળાંકો છે, પરંતુ, જેમ તેઓ કહે છે, તમે પૂરતી કલા મેળવી શકતા નથી, તેથી મેં એવા ઉદાહરણો પસંદ કર્યા છે જે વાસ્તવિક વ્યવહારિક કાર્યોમાં ઘણી વાર જોવા મળે છે.

પ્રથમ, સૌથી સરળ સમીકરણો અને સરળ રેખાઓ:

ફોર્મનું સમીકરણ ધ્રુવમાંથી નીકળતું એક સ્પષ્ટ કરે છે બીમ. ખરેખર, તે વિશે વિચારો, જો કોણ મૂલ્ય હંમેશા(જે પણ "er" છે) સતત, પછી તે કઈ રેખા છે?

નોંધ : સામાન્યકૃત ધ્રુવીય સંકલન પ્રણાલીમાં આપેલ સમીકરણધ્રુવમાંથી પસાર થતી સીધી રેખાને વ્યાખ્યાયિત કરે છે

ફોર્મનું સમીકરણ નક્કી કરે છે... પ્રથમ વખત અનુમાન કરો - જો કોઈપણ માટેકોણ "ફી" ત્રિજ્યા સ્થિર રહે છે? હકીકતમાં આ વ્યાખ્યા છે વર્તુળત્રિજ્યાના ધ્રુવ પર કેન્દ્રિત.

ઉદાહરણ તરીકે, . સ્પષ્ટતા માટે, ચાલો આ રેખાના સમીકરણને લંબચોરસ સંકલન પ્રણાલીમાં શોધીએ. પાછલા ફકરામાં મેળવેલ સૂત્રનો ઉપયોગ કરીને, અમે રિપ્લેસમેન્ટ કરીએ છીએ:

ચાલો બંને બાજુઓને ચોરસ કરીએ:

– વર્તુળનું સમીકરણત્રિજ્યા 2 ના મૂળમાં કેન્દ્ર સાથે, જે તપાસવાની જરૂર છે.

લેખની રચના અને પ્રકાશન ત્યારથી રેખીય અવલંબન અને વેક્ટર્સની રેખીય સ્વતંત્રતા વિશેમને સાઇટના મુલાકાતીઓ તરફથી ઘણા પત્રો મળ્યા જેમણે આની ભાવનામાં પ્રશ્ન પૂછ્યો: "ત્યાં એક સરળ અને અનુકૂળ લંબચોરસ સંકલન પ્રણાલી છે, અમને બીજી ત્રાંસી શા માટે જરૂર છે?" affine કેસ?. જવાબ સરળ છે: ગણિત બધું અને દરેકને સ્વીકારવાનો પ્રયત્ન કરે છે! વધુમાં, આપેલ પરિસ્થિતિમાં, સગવડતા મહત્વપૂર્ણ છે - જેમ તમે જોઈ શકો છો, સમીકરણની અત્યંત સરળતાને કારણે ધ્રુવીય કોઓર્ડિનેટ્સમાં વર્તુળ સાથે કામ કરવું વધુ નફાકારક છે.

અને ક્યારેક ગાણિતિક મોડેલઅપેક્ષા રાખે છે વૈજ્ઞાનિક શોધો. તેથી, એક સમયે કાઝાન યુનિવર્સિટીના રેક્ટર એન.આઈ. લોબાચેવ્સ્કી સખત રીતે સાબિત, મારફતે મનસ્વી બિંદુવિમાનો દોરી શકાય છે અનંત ઘણી સીધી રેખાઓ, આની સમાંતર. પરિણામે, તેની બદનામી થઈ વૈજ્ઞાનિક વિશ્વ, પરંતુ... ખંડન આ હકીકતકોઈ કરી શક્યું નહીં. માત્ર એક સારી સદી પછી, ખગોળશાસ્ત્રીઓએ શોધ્યું કે અવકાશમાં પ્રકાશ વક્ર માર્ગો સાથે પ્રવાસ કરે છે, જ્યાં લોબાચેવ્સ્કીની બિન-યુક્લિડિયન ભૂમિતિ, આ શોધના ઘણા સમય પહેલા તેમના દ્વારા ઔપચારિક રીતે વિકસાવવામાં આવી હતી, કામ કરવાનું શરૂ કરે છે. એવું માનવામાં આવે છે કે આ પોતે અવકાશની મિલકત છે, જેની વક્રતા નાના (ખગોળશાસ્ત્રીય ધોરણો દ્વારા) અંતરને કારણે આપણા માટે અદ્રશ્ય છે.

ચાલો વધુ અર્થપૂર્ણ બાંધકામ કાર્યોને ધ્યાનમાં લઈએ:

ઉદાહરણ 2

એક લાઇન બનાવો

ઉકેલ: સૌ પ્રથમ, ચાલો શોધીએ વ્યાખ્યાનું ક્ષેત્ર. ધ્રુવીય ત્રિજ્યા બિન-નકારાત્મક હોવાથી, અસમાનતા હોવી આવશ્યક છે. તમે ત્રિકોણમિતિ અસમાનતાઓને ઉકેલવા માટેના શાળાના નિયમો યાદ રાખી શકો છો, પરંતુ માં સરળ કિસ્સાઓઆની જેમ, હું ઝડપી ભલામણ કરું છું અને દ્રશ્ય પદ્ધતિઉકેલો:

કોસાઇન ગ્રાફની કલ્પના કરો. જો તે હજી સુધી તમારી મેમરીમાં નોંધાયેલ નથી, તો પછી તેને પૃષ્ઠ પર શોધો પ્રાથમિક કાર્યોનો આલેખ. અસમાનતા આપણને શું કહે છે? તે અમને કહે છે કે કોસાઇન ગ્રાફ સ્થિત હોવો જોઈએ નીચું નથી abscissa અક્ષ. અને આ સેગમેન્ટ પર થાય છે. અને, તે મુજબ, અંતરાલ યોગ્ય નથી.

આમ, આપણા કાર્યની વ્યાખ્યાનું ડોમેન છે: , એટલે કે, ગ્રાફ ધ્રુવની જમણી બાજુએ સ્થિત છે (કાર્ટેશિયન સિસ્ટમની પરિભાષામાં - જમણા અડધા પ્લેનમાં).

ધ્રુવીય કોઓર્ડિનેટ્સમાં, ઘણી વખત કોઈ અસ્પષ્ટ વિચાર હોય છે કે કઈ રેખા ચોક્કસ સમીકરણને વ્યાખ્યાયિત કરે છે, તેથી તેને બાંધવા માટે, તમારે તેની સાથે સંબંધિત બિંદુઓ શોધવાની જરૂર છે - અને વધુ, વધુ સારું. સામાન્ય રીતે તેઓ એક ડઝન કે બે (અથવા તેનાથી ઓછા) સુધી મર્યાદિત હોય છે. સૌથી સહેલો રસ્તો, અલબત્ત, લેવાનો છે કોષ્ટક કોણ મૂલ્યો. વધુ સ્પષ્ટતા માટે, નકારાત્મક મૂલ્યોહું એક વળાંક "સ્ક્રૂ" કરીશ:

કોસાઇનની સમાનતાને કારણે સંબંધિત હકારાત્મક મૂલ્યોતમારે ફરીથી ગણતરી કરવાની જરૂર નથી:

ચાલો આપણે ધ્રુવીય સંકલન પ્રણાલીનું નિરૂપણ કરીએ અને મળેલા બિંદુઓને કાવતરું કરીએ, જ્યારે સમાન મૂલ્યોઉપર ચર્ચા કરેલ ટેક્નોલોજીનો ઉપયોગ કરીને હોકાયંત્ર સાથે જોડી બનાવીને, એક સમયે “er” બંધ કરવું અનુકૂળ છે:

સૈદ્ધાંતિક રીતે, રેખા સ્પષ્ટ રીતે દોરવામાં આવી છે, પરંતુ અનુમાનની સંપૂર્ણ પુષ્ટિ કરવા માટે, ચાલો તેનું સમીકરણ કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમમાં શોધીએ. તમે તાજેતરમાં મેળવેલા સૂત્રો લાગુ કરી શકો છો , પરંતુ હું તમને વધુ ઘડાયેલ યુક્તિ વિશે કહીશ. અમે કૃત્રિમ રીતે સમીકરણની બંને બાજુઓને “er” વડે ગુણાકાર કરીએ છીએ: અને વધુ કોમ્પેક્ટ સંક્રમણ સૂત્રોનો ઉપયોગ કરીએ છીએ:

હાઇલાઇટિંગ સંપૂર્ણ ચોરસ, અમે રેખાના સમીકરણને ઓળખી શકાય તેવા સ્વરૂપમાં લાવીએ છીએ:

– વર્તુળનું સમીકરણબિંદુ પર કેન્દ્ર સાથે, ત્રિજ્યા 2.

કારણ કે શરત અનુસાર બાંધકામ હાથ ધરવા માટે તે ફક્ત જરૂરી હતું અને તે જ છે, અમે મળી આવેલા બિંદુઓને એક લીટી સાથે સરળતાથી જોડીએ છીએ:

તૈયાર છે. જો તે થોડું અસમાન હોય તો ઠીક છે, તમારે જાણવાની જરૂર નથી કે તે એક વર્તુળ હતું ;-)

શા માટે આપણે અંતરાલની બહારના ખૂણાના મૂલ્યોને ધ્યાનમાં લીધા નથી? જવાબ સરળ છે: ત્યાં કોઈ અર્થ નથી. કાર્યની સામયિકતાને લીધે, આપણે બાંધેલા વર્તુળ સાથે અનંત દોડનો સામનો કરીએ છીએ.

સરળ વિશ્લેષણ હાથ ધરવું અને નિષ્કર્ષ પર આવવું સરળ છે કે ફોર્મનું સમીકરણ બિંદુ પર કેન્દ્ર સાથે વ્યાસનું વર્તુળ સ્પષ્ટ કરે છે. અલંકારિક રીતે કહીએ તો, આવા તમામ વર્તુળો ધ્રુવીય ધરી પર "બેસે છે" અને આવશ્યકપણે ધ્રુવમાંથી પસાર થાય છે. જો પછી મનોરંજક કંપનીડાબી તરફ સ્થળાંતર કરશે - ધ્રુવીય અક્ષની ચાલુ રાખવા માટે (શા માટે તે વિશે વિચારો).

માટે સમાન કાર્ય સ્વતંત્ર નિર્ણય:

ઉદાહરણ 3

એક રેખા બનાવો અને તેનું સમીકરણ લંબચોરસ કોઓર્ડિનેટ સિસ્ટમમાં શોધો.

ચાલો સમસ્યાને ઉકેલવા માટેની પ્રક્રિયાને વ્યવસ્થિત કરીએ:

સૌ પ્રથમ, આપણે કાર્યની વ્યાખ્યાનું ડોમેન શોધીએ છીએ આ માટે તે જોવાનું અનુકૂળ છે સાઇનસૉઇડતરત જ સમજવા માટે કે સાઈન ક્યાં બિન-નેગેટિવ છે.

બીજા પગલામાં, આપણે પોઈન્ટના ધ્રુવીય કોઓર્ડિનેટ્સનો ઉપયોગ કરીને ગણતરી કરીએ છીએ કોષ્ટક કોણ મૂલ્યો; વિશ્લેષણ કરો કે ગણતરીઓની સંખ્યા ઘટાડવી શક્ય છે કે કેમ?

ત્રીજા પગલામાં, અમે ધ્રુવીય સંકલન પ્રણાલીમાં બિંદુઓને કાવતરું કરીએ છીએ અને કાળજીપૂર્વક તેમને એક રેખા સાથે જોડીએ છીએ.

અને અંતે, આપણે કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમમાં રેખાનું સમીકરણ શોધીએ છીએ.

અંદાજિત નમૂનાપાઠના અંતે ઉકેલો.

સામાન્ય અલ્ગોરિધમનોઅને અમે ધ્રુવીય કોઓર્ડિનેટ્સમાં બાંધકામ તકનીકની વિગત આપીએ છીએ
અને નોંધપાત્ર રીતે ઝડપીવ્યાખ્યાનના બીજા ભાગમાં, પરંતુ તે પહેલાં આપણે બીજી સામાન્ય લાઇનથી પરિચિત થઈશું:

ધ્રુવીય ગુલાબ

તે સાચું છે, અમે પાંખડીઓવાળા ફૂલ વિશે વાત કરી રહ્યા છીએ:

ઉદાહરણ 4

ધ્રુવીય કોઓર્ડિનેટ્સમાં સમીકરણો દ્વારા આપવામાં આવેલી રેખાઓ બનાવો

ધ્રુવીય ગુલાબ બનાવવા માટે બે અભિગમો છે. સૌપ્રથમ, ચાલો ધ્રુવીય ત્રિજ્યા નેગેટિવ ન હોઈ શકે એમ માનીને, નુર્લ્ડ ટ્રેકને અનુસરીએ:

ઉકેલ:

a) ચાલો ફંક્શનની વ્યાખ્યાનું ડોમેન શોધીએ:

આ ત્રિકોણમિતિ અસમાનતાગ્રાફિકલી હલ કરવી પણ મુશ્કેલ નથી: લેખની સામગ્રીમાંથી આલેખનું ભૌમિતિક પરિવર્તનતે જાણીતું છે કે જો ફંક્શનની દલીલ બમણી કરવામાં આવે છે, તો તેનો ગ્રાફ ઓર્ડિનેટ અક્ષ પર 2 ગણો સંકોચાઈ જશે. કૃપા કરીને પ્રથમ ઉદાહરણમાં ફંક્શનનો ગ્રાફ શોધો ઉલ્લેખિત પાઠ. આ સાઇનસૉઇડ x-અક્ષની ઉપર ક્યાં સ્થિત છે? અંતરાલોમાં . તેથી, અસમાનતા અનુરૂપ વિભાગો દ્વારા સંતુષ્ટ છે, અને વ્યાખ્યાનું ક્ષેત્રઅમારું કાર્ય: .

સામાન્ય રીતે કહીએ તો, વિચારણા હેઠળની અસમાનતાઓનો ઉકેલ એ સંઘ છે અનંત સંખ્યાસેગમેન્ટ્સ, પરંતુ, ફરીથી, અમને ફક્ત એક જ સમયગાળામાં રસ છે.

કદાચ કેટલાક વાચકોને તે સરળ લાગશે વિશ્લેષણાત્મક પદ્ધતિવ્યાખ્યાના ડોમેનને શોધીને, હું તેને શરતી રીતે "ગોળ પાઇ કાપી નાખવું" કહીશ. અમે કાપીશું સમાન ભાગોમાંઅને, સૌ પ્રથમ, પ્રથમ ભાગની સીમાઓ શોધો. અમે નીચે મુજબ કારણ આપીએ છીએ: સાઈન બિન-નકારાત્મક છે, જ્યારે તેની દલીલ 0 થી rad સુધીની રેન્જ. સમાવિષ્ટ અમારા ઉદાહરણમાં: . ડબલ અસમાનતાના તમામ ભાગોને 2 વડે વિભાજીત કરીને, અમે જરૂરી અંતરાલ મેળવીએ છીએ:

હવે આપણે ક્રમિક રીતે "90 ડિગ્રીના સમાન ટુકડાઓ" ઘડિયાળની વિરુદ્ધ દિશામાં કાપવાનું શરૂ કરીએ છીએ:

- મળેલ સેગમેન્ટ, અલબત્ત, વ્યાખ્યાના ક્ષેત્રમાં શામેલ છે;

- આગામી અંતરાલ - શામેલ નથી;

- આગામી સેગમેન્ટ - સમાવિષ્ટ;

– અને અંતે, અંતરાલ – સમાવેલ નથી.

ડેઝીની જેમ - “પ્રેમ કરે છે, પ્રેમ નથી કરતા, પ્રેમ કરે છે, પ્રેમ નથી કરતા” =) એ તફાવત સાથે કે અહીં કોઈ નસીબ કહેવાનું નથી. હા, ચાઇનીઝમાં તે માત્ર એક પ્રકારનો પ્રેમ છે….

તેથી, અને રેખા બે સરખા પાંખડીઓ સાથે ગુલાબનું પ્રતિનિધિત્વ કરે છે. ડ્રોઇંગને યોજનાકીય રીતે દોરવા માટે તે તદ્દન સ્વીકાર્ય છે, પરંતુ તે યોગ્ય રીતે શોધવા અને ચિહ્નિત કરવા માટે ખૂબ સલાહભર્યું છે પાંદડીઓની ટોચ. શિરોબિંદુઓ અનુલક્ષે છે વ્યાખ્યાના ડોમેનના સેગમેન્ટ્સના મધ્યબિંદુઓ, જેમાં આ ઉદાહરણમાંસ્પષ્ટ કોણીય કોઓર્ડિનેટ્સ છે . તે જ સમયે પાંખડીની લંબાઈછે:

સંભાળ રાખનાર માળીનું કુદરતી પરિણામ અહીં છે:

એ નોંધવું જોઈએ કે પાંખડીની લંબાઈ સમીકરણમાંથી સરળતાથી જોઈ શકાય છે - કારણ કે સાઈન મર્યાદિત છે: , પછી મહત્તમ મૂલ્ય"er" ચોક્કસપણે બે કરતાં વધી જશે નહીં.

બી) ચાલો એક લાઇન બનાવીએ, સમીકરણ દ્વારા આપવામાં આવે છે. દેખીતી રીતે, આ ગુલાબની પાંખડીની લંબાઈ પણ બે છે, પરંતુ, સૌ પ્રથમ, અમને વ્યાખ્યાના ક્ષેત્રમાં રસ છે. લાગુ વિશ્લેષણાત્મક પદ્ધતિ"કટ્સ": જ્યારે તેની દલીલ હોય ત્યારે સાઈન બિન-નકારાત્મક હોય છેશૂન્યથી "pi" સહિતની શ્રેણીમાં છે, માં આ કિસ્સામાં: . અમે અસમાનતાના તમામ ભાગોને 3 વડે વિભાજીત કરીએ છીએ અને પ્રથમ અંતરાલ મેળવીએ છીએ:

આગળ, અમે રેડ દ્વારા "પાઇને ટુકડાઓમાં કાપવાનું" શરૂ કરીએ છીએ. (60 ડિગ્રી):
- સેગમેન્ટ વ્યાખ્યા ડોમેન દાખલ કરશે;
- અંતરાલ - શામેલ કરવામાં આવશે નહીં;
- સેગમેન્ટ - ફિટ થશે;
- અંતરાલ - શામેલ કરવામાં આવશે નહીં;
- સેગમેન્ટ - ફિટ થશે;
- અંતરાલ - શામેલ કરવામાં આવશે નહીં.

પ્રક્રિયા સફળતાપૂર્વક 360 ડિગ્રી પર પૂર્ણ થાય છે.

આમ, વ્યાખ્યાનો અવકાશ છે: .

સંપૂર્ણ અથવા આંશિક રીતે હાથ ધરવામાં આવેલી ક્રિયાઓ માનસિક રીતે હાથ ધરવા માટે સરળ છે.

બાંધકામ. જો પાછલા ફકરામાં જમણા ખૂણા અને 45 ડિગ્રીના ખૂણાઓ સાથે બધું સારી રીતે કામ કરે છે, તો અહીં તમારે થોડું ટિંકર કરવું પડશે. ચાલો શોધીએ પાંદડીઓની ટોચ. તેમની લંબાઈ કાર્યની શરૂઆતથી જ દેખાતી હતી;

મહેરબાની કરીને નોંધ કરો કે પાંખડીઓની ટોચ વચ્ચે સમાન જગ્યાઓ હોવી જોઈએ, આ કિસ્સામાં 120 ડિગ્રી.

ડ્રોઇંગને 60-ડિગ્રી સેક્ટરમાં ચિહ્નિત કરવાની સલાહ આપવામાં આવે છે (સીમાંકિત લીલી રેખાઓ) અને પાંખડીઓના શિરોબિંદુઓની દિશાઓ દોરો (ગ્રે રેખાઓ). હોકાયંત્રનો ઉપયોગ કરીને શિરોબિંદુઓને પોતાને ચિહ્નિત કરવું અનુકૂળ છે - એકવાર 2 એકમોનું અંતર માપો અને 30, 150 અને 270 ડિગ્રીની દોરેલી દિશામાં ત્રણ નોચ બનાવો:

તૈયાર છે. હું સમજું છું કે આ એક મુશ્કેલીભર્યું કાર્ય છે, પરંતુ જો તમે બધું સમજદારીપૂર્વક ગોઠવવા માંગતા હો, તો તમારે સમય પસાર કરવો પડશે.

ચાલો ઘડીએ સામાન્ય સૂત્ર : ફોર્મનું સમીકરણ , એક કુદરતી સંખ્યા છે), ધ્રુવીય-પાંખડીવાળા ગુલાબને વ્યાખ્યાયિત કરે છે, જેની પાંખડીની લંબાઈ બરાબર છે.

ઉદાહરણ તરીકે, સમીકરણ 5 એકમોની પાંખડીની લંબાઈ સાથે ક્વાટ્રેફોઈલનો ઉલ્લેખ કરે છે, સમીકરણ 3 એકમોની પાંખડીની લંબાઈ સાથે 5-પાંખડીવાળા ગુલાબનો ઉલ્લેખ કરે છે. વગેરે