Gizemli bozukluk: Fraktalların tarihi ve uygulama alanları. Asal sayılarda fraktallar

giriiş

Fraktal kavramı................................................. ......................................................4

Fraktalların ortaya çıkış tarihi………………………………………………………..6

Cebirsel fraktallar………………..…………………………….8

1. Maldebrod seti………………………………………………9

   Julia seti……………………………………………………11

   Newton havuzları (fraktallar)……………………………………………………13

   Fraktal (kabarcıklar) Halley……………………………………………..14

Pratik Uygulama fraktallar……………………………………...15

Sonuç………………………………………………………………………………….19

Referans listesi……………………………………………………………………20

giriiş

Bilimin dili hızla değişiyor modern dünya. Fiziğin gelişiminin tarihi bir asırdan daha eskilere dayanmaktadır. Bu süre zarfında çok sayıda farklı doğa olayı incelendi, çeşitli deneysel gerçekleri açıklayan temel fizik yasaları keşfedildi.

Doğadaki çoğu sistem iki özelliği birleştirir: Birincisi, çok büyüktürler, genellikle çok yönlüdürler, çeşitlidirler ve karmaşıktırlar ve ikinci olarakçok etkisi altında oluşurlar Olumsuz büyük miktarlar basit kalıplar ve bu basit kalıplara uyarak daha da gelişin. Bunlar en çok farklı sistemler kristallerden ve basit kümelerden (bulutlar, nehirler, dağlar, kıtalar, yıldızlar gibi çeşitli birikim türleri) başlayıp ekosistemler ve biyolojik nesneler(eğreltiotu yaprağından insan beyni). Fraktallar tam da bu tür nesnelerdir: bir yandan karmaşık (sonsuz sayıda öğe içeren), diğer yandan çok uygun bir şekilde inşa edilmiş basit yasalar. Bu özelliği sayesinde fraktalların birçok doğal nesneyle pek çok ortak noktası vardır. Ancak fraktal şununla olumlu şekilde karşılaştırır: doğal nesne bir fraktalın katı bir matematiksel tanıma sahip olması ve kendisini katı bir tanımlama ve analize uygun hale getirmesi. Bu nedenle fraktal teorisi, bitki kök sistemlerinin büyüme hızını, bataklıkların kurutulması için işçilik maliyetlerini, saman kütlesinin sürgün yüksekliğine bağımlılığını ve çok daha fazlasını tahmin etmeyi mümkün kılar. Bu matematikte yeni bir yöndür ve bilimsel paradigmaönem açısından görelilik teorisiyle karşılaştırılabilecek bir devrim ve kuantum mekaniği. Fraktal geometrinin nesneleri kendi yollarıyla dış görünüş alıştığımız “normal” geometrik şekillerden oldukça farklı. Aslında bu bir atılım matematiksel açıklama uzun süredir böyle bir tanımlamaya uygun olmayan sistemler.

Fraktal geometri “saf” değildir geometrik teori. Bu daha çok bir kavram yeni görünüm iyi bilinen şeyler üzerinde algının yeniden yapılandırılması, araştırmacıyı dünyayı yeni bir şekilde görmeye zorluyor.

Çalışmamın amacı “fraktal” kavramı ve onun çeşitliliği “cebirsel fraktal” hakkında bilgi sahibi olmaktır.

Fraktal kavramı

Nispeten yakın zamanda, matematikte, daha hacimli, ancak yine de bir çizgiye benzeyen bir nesnenin görüntüsü ortaya çıktı. Bazı bilim adamları, genişliği olmayan bir çizgi kavramını kabul etmekte zorlandılar, bu yüzden yavaş yavaş çizgiyi incelemeye başladılar. geometrik şekiller ve kesirli uzaysal boyuta sahip yapılar. Tüm türevleri olan sürekli eğrilerin yerini kırık veya çok pürüzlü eğriler aldı. Böyle bir eğrinin çarpıcı bir örneği Brown parçacığının yörüngesidir. Bilimde fraktal kavramı bu şekilde ortaya çıktı.

Fraktal(lat. fractus - ezilmiş, kırılmış, kırılmış) - karmaşık geometrik şekil kendine benzerlik özelliğine sahip olan, yani her biri şeklin tamamına benzeyen birkaç parçadan oluşan (Şekil 1). Daha fazla geniş anlamda Fraktallar, Öklid uzayında kesirli metrik boyuta (Minkowski veya Hausdorff anlamında) veya metrik boyuta sahip nokta kümeleri olarak anlaşılır.

Pirinç. 1
"Fraktal" kelimesinin olmadığı unutulmamalıdır. matematik terimi ve genel olarak kabul edilmiş katı bir kuralları yoktur matematiksel tanım. Söz konusu şekil aşağıdaki özelliklerden herhangi birine sahip olduğunda kullanılabilir:

Her ölçekte önemsiz olmayan bir yapıya sahiptir. Bu, normal şekillerin (daire, elips, grafik gibi) tersidir. pürüzsüz fonksiyon): Düzenli bir şeklin küçük bir parçasına çok büyük ölçekte bakarsak, düz bir çizginin parçası gibi görünecektir. Bir fraktal için ölçeğin arttırılması yapının basitleştirilmesine yol açmaz; tüm ölçeklerde eşit derecede karmaşık bir resim göreceğiz.

Kendine benzer veya yaklaşık olarak kendine benzer.

Kesirli bir metrik boyutu vardır.

Doğadaki pek çok nesnenin fraktal özellikleri vardır; örneğin kıyılar, bulutlar, ağaç taçları, dolaşım sistemi ve insanlarda veya hayvanlarda alveolar sistem.
Fraktallar, özellikle düzlem üzerinde, güzelliğin bilgisayar kullanılarak yapım kolaylığı ile birleşimi nedeniyle popülerdir.

Fraktalların tarihi

19. ve 20. yüzyılın başında fraktalların incelenmesi sistematik olmaktan çok epizodikti, çünkü daha önce matematikçiler çoğunlukla kullanılarak çalışılabilecek "iyi" nesneler üzerinde çalışıyordu. ortak yöntemler ve teoriler. 1872'de Alman matematikçi Karl Weierstrass bir örnek oluşturdu. sürekli fonksiyon hiçbir yerde türevi alınamayan, yani hiçbir noktasında teğeti olmayan. Ancak yapısı tamamen soyuttu ve anlaşılması zordu. Bu nedenle 1904 yılında İsveçli Helge von Koch, hiçbir yerde teğeti olmayan ve çizilmesi oldukça kolay olan sürekli bir eğri buldu. Bir fraktalın özelliklerine sahip olduğu ortaya çıktı. Bu eğrinin bir çeşidine “Koch kar tanesi” denir.
Figürlerin kendine benzerliği fikri Fransız Paul Pierre Levy tarafından benimsendi. gelecekteki akıl hocası Benoit Mandelbrot. 1938'de, başka bir fraktal olan Levy C eğrisini tanımlayan “Düzlemsel ve uzaysal eğriler ve bütüne benzer parçalardan oluşan yüzeyler” adlı makalesi yayınlandı. Yukarıda listelenen bu fraktalların tümü, koşullu olarak bir sınıf yapıcı (geometrik) fraktallar olarak sınıflandırılabilir.
Başka bir sınıf, Mandelbrot kümesini içeren dinamik (cebirsel) fraktallardır. Bu yöndeki ilk araştırmalar 20. yüzyılın başında başlamış ve isimlerle ilişkilendirilmiştir. Fransız matematikçiler Gaston Julia ve Pierre Fatu. 1918'de Julia'nın karmaşık tekrarlamalar üzerine çalışması yayınlandı. rasyonel fonksiyonlar Mandelbrot kümesiyle yakından ilişkili bütün bir fraktal ailesi olan Julia kümelerini tanımlar. Bu çalışma ödüle layık görüldü Fransız Akademisi ancak tek bir resim içermediğinden açık nesnelerin güzelliğini takdir etmek imkansızdı.

Fraktal geometrinin ilk fikirleri 19. yüzyılda ortaya çıktı. Cantor, basit bir özyinelemeli (tekrarlayan) prosedür kullanarak, çizgiyi bağlantısız noktalardan oluşan bir koleksiyona (Cantor Tozu olarak adlandırılan) dönüştürdü. Bir çizgi alıp ortadaki üçte birlik kısmı kaldırıyor ve ardından aynı işlemi geri kalan bölümlerle tekrarlıyordu. (Şekil 2)

Pirinç. 2

Peano berabere kaldı özel türçizgiler.(Şek. 3)

Pirinç. 3

Peano bunu çizmek için aşağıdaki algoritmayı kullandı.

İlk adımda düz bir çizgi aldı ve onu orijinal çizginin uzunluğundan 3 kat daha kısa olan 9 parçayla değiştirdi (şeklin 1. ve 2. kısımları). Daha sonra ortaya çıkan çizginin her bölümü için aynısını yaptı. Ve bu sonsuza kadar devam edecek. Çizginin benzersizliği tüm düzlemi doldurmasıdır. Düzlemdeki her noktaya karşılık bir noktanın bulunabileceği kanıtlanmıştır. çizgiye ait Peano.

Peano'nun eğrisi ve Cantor'un tozu sıradan geometrik nesnelerin ötesine geçti. Net bir boyutları yoktu. Cantor'un tozu tek boyutlu bir düz çizgi temelinde inşa edilmiş gibi görünüyordu, ancak noktalardan (boyut 0) oluşuyordu. Ve Peano eğrisi tek boyutlu bir çizgiye dayanarak oluşturuldu ve sonuç bir düzlemdi. Bilimin diğer birçok alanında, yukarıda açıklananlara benzer şekilde, çözümleri garip sonuçlara yol açan sorunlar ortaya çıktı ( Brown hareketi, hisse senedi fiyatları).

20. yüzyıla kadar bu tür veriler garip nesneler, onları sistemleştirmeye yönelik herhangi bir girişimde bulunmadan. Ta ki modern fraktal geometrinin ve fraktal kelimesinin babası Benoit Mandelbrot bunları ele alana kadar. Gerçekleri yavaş yavaş karşılaştırarak matematikte yeni bir yön olan fraktal geometriyi keşfetti.

Bir fraktalı daha net hayal etmek için, B. Mandelbrot'un klasik hale gelen "Doğanın Fraktal Geometrisi" kitabında verilen bir örneği ele alalım - "Britanya kıyılarının uzunluğu nedir?" Bu sorunun cevabı göründüğü kadar basit değil. Her şey kullanılan aletin uzunluğuna bağlıdır. Kıyıyı bir kilometre cetveli kullanarak ölçerek bir miktar uzunluk elde ederler. Ancak ölçülen cetvelden çok daha küçük olan birçok küçük koy ve yarımada gözden kaçırılıyor. Cetvelin boyutunun 1 metreye düşürülmesiyle sahil uzunluğunun uzayacağı ortaya çıkıyor. Bir milimetre cetvel kullanarak bankanın uzunluğunu ölçerken, bir milimetreden daha büyük parçalar dikkate alındığında uzunluk daha da büyük olacaktır. Sonuç olarak, görünüşte basit bir sorunun cevabı herkesi şaşırtabilir - Britanya kıyılarının uzunluğu sonsuzdur.

Cebirsel fraktallar

Cebirsel fraktallar bu temel üzerine inşa edildikleri için bu ismi almıştır. cebirsel formüller. Cebirsel fraktallar elde etmek için çeşitli yöntemler vardır. Yöntemlerden biri fonksiyonun tekrarlı hesaplanmasıdır; buradaz - karmaşık sayı ve f belirli bir fonksiyondur. Bu fonksiyonun hesaplanması belirli bir koşul sağlanana kadar devam eder. Ve bu koşul karşılandığında ekranda bir nokta görüntülenir. Bu durumda fonksiyon değerleri farklı noktalar karmaşık düzlem olabilir farklı davranış:

zamanla sonsuza doğru yönelir;

0'a eğilimlidir;
birkaç sabit değer alır ve bunların ötesine geçmez;
davranış kaotiktir ve herhangi bir eğilim yoktur.

3.1 Mandelbrot kümesi

Mandelbrot seti (en ünlü fraktal nesnelerden biri) ilk kez 1980 baharında Benoit Mandelbrot tarafından (görsel olarak bir bilgisayar kullanılarak) inşa edildi. araştırma merkezi IBM şirketinin adı. Thomas J. Watson. Her ne kadar bu tür nesnelere yönelik araştırmalar geçen yüzyılda başlamış olsa da, bu setin keşfi ve donanımın geliştirilmesiyle gerçekleşti. bilgisayar grafikleri V belirleyici derece Fraktal geometrinin ve kaos teorisinin gelişimini etkiledi. Peki Mandelbrot kümesi nedir?

Karmaşık bir değişkenin işlevini düşünün. Hadi koyalımve sırayı göz önünde bulundurun, nerede olursa olsun. Böyle bir dizi sınırlanabilir (yani herhangi bir dizi için öyle bir r olabilir ki)) veya “sonsuzluğa kaçmak” (yani herhangi bir r > 0 için). Mandelbrot kümesi, belirtilen dizinin sınırlandığı c karmaşık sayılar kümesi olarak tanımlanabilir. Ne yazık ki bilinmiyor analitik ifade Bu, belirli bir c'nin Mandelbrot kümesine ait olup olmadığını belirlemesine olanak tanır. Bu nedenle, bir küme oluşturmak için bir bilgisayar deneyi kullanılır: karmaşık düzlemdeki bir dizi noktaya belirli bir adımla bakarlar ve gerçekleştirdikleri her nokta için belli bir sayı yinelemeler yapın (dizinin belirli sayıda üyesini bulun) ve "davranışını" izleyin. (Şekil 4).

Mandelbrot kümesinin, merkezi orijinde olan r=2 yarıçaplı bir çember üzerinde yer aldığı kanıtlanmıştır. Dolayısıyla, eğer herhangi bir adımda dizinin bir sonraki teriminin modülü 2'yi aşarsa, bu diziyi tanımlayan c'ye karşılık gelen noktanın Mandelbrot kümesine ait olmadığı sonucuna hemen varabiliriz.

Karmaşık sayıların tarandığı adımı azaltarak ve yineleme sayısını artırarak istediğimiz kadar ayrıntılı, ancak her zaman kümenin yalnızca yaklaşık görüntülerini elde edebiliriz.

Elimizde kesinlik için 0'dan N-1'e kadar numaralandırılmış N renk olsun. Kesinlik açısından yine siyah rengin 0 sayısına sahip olduğunu varsayacağız. Eğer belirli bir c için N-1 yinelemeden sonra nokta yarıçapı 2 olan dairenin ötesine geçmiyorsa, c'nin Mandelbrot kümesine ait olduğunu varsayacağız ve bunu boyayacağız c noktası siyah. Aksi takdirde, k adımında (k ) bir sonraki nokta yarıçap 2 çemberinin dışına çıkarsa (yani, k'inci adımda onun "kaçtığını" fark ettik), onu k rengine boyayacağız.

Güzel görüntüler elde edildiğinde iyi seçim setin paletleri ve mahalleleri (yani setin dışında “renkli noktalar” elde edeceğiz) (Şekil 5, 6).

Pirinç. 4

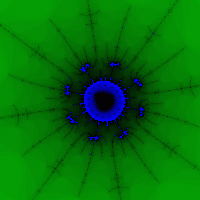
Pirinç. 5 Şek. 6

3.2 Julia seti

Mandelbrot kümesiyle yakından ilişkili olan Julia kümeleri, 20. yüzyılın başında matematikçiler Gaston Julia ve Pierre Fatou tarafından incelenmiştir (bkz.). 1917-1919'da karmaşık bir değişkenin fonksiyonlarının yinelenmesiyle ilgili temel sonuçlar elde ettiler. Genel olarak konuşursak, bu gerçek ayrı bir tartışmayı hak ediyor ve etkileyici bir örnek. matematiksel araştırma, zamanının onlarca yıl ilerisinde (bilim adamları, üzerinde çalıştıkları nesnelerin neye benzediğini yalnızca yaklaşık olarak hayal edebiliyorlardı!), ancak biz yalnızca karmaşık değişkenli bir fonksiyon için Julia kümelerini oluşturmanın bir yöntemini tanımlayacağız.. Daha doğrusu sözde inşa edeceğiz. "Julia setlerini dolduruyorum".

Bir dikdörtgen düşünün (x 1 ;y 1 )-(X 2 ;y 2 ). Şimdi c sabitini sabitleyelim ve seçilen dikdörtgenin noktalarını belirli bir adımla görüntülemeye başlayalım. Mandelbrot kümesini oluştururken olduğu gibi her nokta için bir dizi yineleme gerçekleştireceğiz (daha sonra daha büyük sayı yinelemeler ne kadar doğru olursa, küme o kadar doğru elde edilecektir). Bir dizi yinelemeden sonra nokta 2 yarıçaplı dairenin sınırının ötesine "kaçmazsa", onu siyah renkle, aksi takdirde paletten bir renkle boyayacağız. (Şekil 7, 8, 9, 10).

Pirinç. 7

Şekil 8 Şekil. 9

Pirinç. 10

3.3 Newton havuzları (fraktallar)

Dinamik fraktalların bir başka türü de Newton fraktallarıdır (havzalar olarak adlandırılır). (Şekil 11). Yapımlarına yönelik formüller çözüm yöntemine dayanmaktadır. doğrusal olmayan denklemler 17. yüzyılda büyük matematikçi tarafından icat edildi. Başvuruyor genel formül Newton'un yöntemi zn+1 = zn - f (zn)/f"(zn), n=0, 1, 2... f(x)=0 denklemini zk-a polinomuna çözmek için bir nokta dizisi elde ederiz : zn+1 = (k-1)znk/kznk-1, n=0, 1, 2... Başlangıç ​​yaklaşımları olarak çeşitli z0 karmaşık sayılarını seçerek, bu polinomun köklerine yakınsayan diziler elde edeceğiz. tam olarak k köke sahipse, tüm düzlem k parçaya bölünmüştür - köklerin çekim alanları bu parçaların sınırları fraktal bir yapıya sahiptir.

Pirinç. 11

3.4 Fraktal (kabarcıklar) Halley

Bu tür fraktallar, dinamik bir fraktal oluşturmak için kural olarak, bir fonksiyonun köklerinin yaklaşık değerlerini bulmak için Halley formülünü kullanırsanız elde edilir. (Şekil 12).

Yöntem bir dizi yinelemeden oluşur:

Yöntemin fikri, dinamik fraktallar çizmek için kullanılanla hemen hemen aynıdır: başlangıç ​​değeri(her zamanki gibi konuşuyoruz değişkenlerin ve fonksiyonların değerleri) ve formülü birçok kez uygulayarak bir sayı dizisi elde edin. Neredeyse her zaman fonksiyonun sıfırlarından birine (yani fonksiyonun 0 değerini aldığı değişkenin değerine) yakınsar. Halley'in yöntemi, hantal formüle rağmen işe yarıyor yöntemden daha etkili : Dizi sıfır fonksiyonlara daha hızlı yakınsar.

Pirinç. 12

Fraktalların pratik uygulaması

Fraktallar her şeyi bulur daha fazla uygulama bilimde. Bunun temel nedeni, açıklamalarıdır. gerçek dünya bazen geleneksel fizik veya matematikten bile daha iyidir. İşte bazı örnekler.

Bilgisayar sistemleri

Bir bilgisayarın oluşturabileceği tüm resimlerden çok azı fraktal görüntülerle rekabet edebilir. hakkında konuşuyoruz gerçek güzellik hakkında.

En yararlı kullanım Bilgisayar bilimindeki fraktallar, fraktal veri sıkıştırmasıdır. Bu tür sıkıştırma, gerçek dünyanın fraktal geometri tarafından iyi tanımlandığı gerçeğine dayanmaktadır. Aynı zamanda görseller geleneksel yöntemlerle (jpeg veya gif gibi) çok daha iyi sıkıştırılır. Fraktal sıkıştırmanın bir diğer avantajı ise görüntü büyütüldüğünde pikselleşme etkisinin (noktaların boyutunun görüntüyü bozacak boyutlara çıkarılması) olmamasıdır. Fraktal sıkıştırmayla, büyütme sonrasında resim genellikle eskisinden daha iyi görünür.

Akışkanlar mekaniği

Akışlardaki türbülans çalışması çok iyi uyarlanmıştır.

fraktallar. Türbülanslı akışlar kaotiktir ve bu nedenle doğru bir şekilde modellenmesi zordur. Ve burada, mühendislerin ve fizikçilerin çalışmalarını büyük ölçüde kolaylaştıran ve karmaşık akışların dinamiklerini daha iyi anlamalarını sağlayan fraktal temsile geçiş yardımcı oluyor.

Fraktalları kullanarak alevleri de simüle edebilirsiniz.

Gözenekli malzemeler, çok karmaşık bir geometriye sahip olmaları nedeniyle fraktal biçimde iyi temsil edilir. Petrol biliminde kullanılır.

Telekomünikasyon

Verilerin uzak mesafelere iletilmesi için antenler kullanılır.

boyutlarını ve ağırlıklarını büyük ölçüde azaltan fraktal şekiller. Fraktallar yüzeylerin eğriliğini tanımlamak için kullanılır. Pürüzlü bir yüzey, iki farklı fraktalın birleşimiyle karakterize edilir.
İlaç

Biyosensör etkileşimleri. Kalp atışı.
Biyoloji

Kaotik süreçlerin modellenmesi, özellikle de popülasyon modellerinin açıklanmasında.
Nanoteknoloji

Nanoteknoloji durumunda fraktallar da rol oynuyor önemli rol Hiyerarşik öz-örgütlenmeleri nedeniyle birçok nanosistem tamsayı olmayan bir boyuta sahiptir, yani geometrik, fizikokimyasal veya işlevsel doğaları itibarıyla fraktallardır. Örneğin, parlak bir örnek kimyasal fraktal sistemler moleküllerdir "dendrimerler » . (Şekil 13)

Pirinç. 13

Edebiyat

Arasında edebi eserler metinsel, yapısal veya anlamsal fraktal yapıya sahip olanları bulun. Metin fraktallarında, metnin öğeleri potansiyel olarak sonsuz bir şekilde tekrarlanır (“Rahibin bir köpeği vardı…”, “Rüyasında bir kelebek olduğunu gören filozofun, rüyasında kendisinin de bir filozof olduğunu rüyasında görmesi…” ve uzantılı metinler (“Jack'in inşa ettiği ev”)

Yapısal fraktallarda metin şeması potansiyel olarak fraktaldır: sone çelengi (15 şiir), sone çelengi (211 şiir), sone çelengi (2455 şiir).

Çözüm

Fraktal, sonsuz karmaşıklığa sahip bir nesnedir ve ayrıntılarının çoğunu uzaktan olduğu kadar yakından da görmenize olanak tanır. Toprak -klasik örnek fraktal nesne. Uzaydan bakıldığında bir top gibi görünüyor. Yaklaşırsak okyanusları, kıtaları, kıyı şeritlerini ve dağ sıralarını bulacağız. Dağlara daha yakından bakalım - daha da ince ayrıntılar görünür hale gelecektir: Dağın yüzeyindeki bir arazi parçası, ölçeği açısından dağın kendisi kadar karmaşık ve düzensizdir. Daha da büyük bir büyütme, her biri fraktal bir nesne olan küçük toprak parçacıklarını ortaya çıkaracaktır.

Sonuç olarak, fraktallar keşfedildikten sonra, birçok bilim adamı için Öklid geometrisinin eski güzel biçimlerinin, içlerinde bazı düzensizlik, düzensizlik ve öngörülemezlik olmaması nedeniyle çoğu doğal nesneden çok daha aşağı olduğunun aşikar hale geldiğini söylemek isterim. Fraktal geometrideki yeni fikirlerin birçok çalışmaya yardımcı olması mümkündür. gizemli olaylar çevreleyen doğa. Fraktallar şu anda fizik, biyoloji, tıp, sosyoloji ve ekonominin birçok alanını hızla istila ediyor. Yeni kavramları kullanan görüntü işleme ve örüntü tanıma yöntemleri, araştırmacıların bu matematiksel aygıtı niceliksel açıklama büyük miktar Doğal nesneler ve yapılar.

Kullanılmış literatür listesi

1. Fraktallara giriş,

2. Zhikov V.V. Julia setlerinde. // Modern doğa bilimi: Ansiklopedi: 10 ciltlik T.1: Matematik. Mekanik. M., 2000.

3. Zhikov V.V. // Modern doğa bilimi: Ansiklopedi: 10 ciltte T.1: Matematik. Mekanik. M., 2000.

4. Mandelbrot B. Doğanın fraktal geometrisi. – M: Bilgisayar Araştırma Enstitüsü, 2002.

5. Morozov M.S. Fraktal teorisine giriş -Moskova-İzhevsk: Bilgisayar Araştırma Enstitüsü, 2002, 160 sayfa.

6. Dinamik (cebirsel) fraktallar // Elementler.. URL'si:http:// basit. ru/ posterler/ fraktallar/ dinamik

7. Dinamik (cebirsel) fraktallar // Elementler.. URL'si:http:// elementy.ru/posters/fractals/Mandelbrot#nop

8. Cebirsel fraktallar // Fraktallar.. URL'si:http://rusproject.narod.ru/article/fractals.htm

Kelebekler elbette yılanlar hakkında hiçbir şey bilmiyorlar. Ama kelebekleri avlayan kuşlar onları biliyor. Yılanları iyi tanımayan kuşların...

(Dinamik) fraktallar

Bu tür fraktallar, doğrusal olmayan dinamik sistemler (dolayısıyla adı) incelenirken ortaya çıkar. Böyle bir sistemin davranışı karmaşık bir şekilde tanımlanabilir. doğrusal olmayan fonksiyon(polinom) f(z). Karmaşık düzlemde z0 başlangıç ​​noktasını alalım. Şimdi karmaşık düzlemde her biri bir öncekinden elde edilen sonsuz bir sayı dizisini düşünün: z0, z1 = f(z0), z2 = f(z1), ... zn+1 = f(zn). bağlı olarak başlangıç ​​noktası z0 böyle bir dizi farklı davranabilir: n → ∞ gibi sonsuza eğilimlidir; bazılarına yakınlaşmak bitiş noktası; döngüsel olarak bir dizi sabit değer alır; Daha karmaşık seçenekler de mümkündür.

Böylece, karmaşık düzlemin herhangi bir z noktası, f(z) fonksiyonunun yinelemeleri sırasında kendi davranışına sahip olur ve tüm düzlem parçalara bölünür. Dahası, bu parçaların sınırlarında yer alan noktalar şu özelliğe sahiptir: keyfi olarak küçük bir yer değiştirmeyle davranışlarının doğası keskin bir şekilde değişir (bu tür noktalara çatallanma noktaları denir). Böylece, belirli bir davranış türüne sahip nokta kümelerinin yanı sıra çatallanma noktaları kümelerinin de sıklıkla fraktal özelliklere sahip olduğu ortaya çıktı. Bunlar f(z) fonksiyonu için Julia kümeleridir.

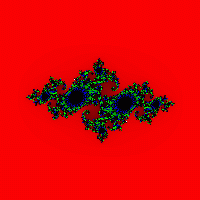
Mandelbrot kümesi biraz farklı şekilde oluşturulmuştur. c'nin karmaşık bir sayı olduğu fc(z) = z2 + c fonksiyonunu düşünün. Bu fonksiyonun z0 = 0 şeklinde bir dizisini oluşturalım; c parametresine bağlı olarak sonsuza kadar ıraksayabilir veya sınırlı kalabilir. Üstelik bu dizinin sınırlı olduğu c'nin tüm değerleri Mandelbrot kümesini oluşturur. Mandelbrot'un kendisi ve diğer matematikçiler tarafından ayrıntılı olarak incelendi ve pek çok şey keşfetti. ilginç özellikler bu çokluğun.

Julia ve Mandelbrot kümelerinin tanımlarının birbirine benzer olduğu görülmektedir. Aslında bu iki grup birbiriyle yakından ilişkilidir. Yani, Mandelbrot kümesi, Julia kümesi fc(z)'nin bağlı olduğu karmaşık c parametresinin tüm değerleridir (bir küme, bazı ek koşullarla iki ayrı parçaya bölünemiyorsa bağlantılı olarak adlandırılır).

Bu en çok büyük grup fraktallar. Doğrusal olmayan süreçler kullanılarak elde edilirler. n boyutlu uzaylar. İki boyutlu süreçler en çok çalışılanlardır. Doğrusal olmayan yinelemeli bir süreci ayrı bir dinamik sistem olarak yorumlarken, bu sistemlerin teorisinin terminolojisi kullanılabilir: faz portresi, kararlı durum süreci, çekici vb.

Doğrusal olmayan dinamik sistemlerin birçok kararlı duruma sahip olduğu bilinmektedir. Belirli sayıda yinelemeden sonra dinamik sistemin kendini bulduğu durum, başlangıç ​​durumuna bağlıdır. Bu nedenle, her kararlı durum (veya dedikleri gibi çekici), sistemin mutlaka söz konusu son durumlara düşeceği belirli bir başlangıç ​​durumları bölgesine sahiptir. Böylece faz uzayı sistem çekicilerin çekim alanlarına bölünmüştür. Faz uzayı iki boyutlu ise çekim alanlarının renklendirilmesi farklı renkler, bu sistemin renkli faz portresini elde edebilirsiniz (yinelemeli süreç). Renk seçim algoritmasını değiştirerek tuhaf çok renkli desenlere sahip karmaşık fraktal desenler elde edebilirsiniz. Matematikçiler için bir sürpriz, ilkel algoritmalar kullanarak çok karmaşık, önemsiz olmayan yapılar üretme yeteneğiydi.

Örnek olarak Mandelbrot kümesini düşünün (bkz. Şekil 3 ve Şekil 4). Yapım algoritması oldukça basittir ve basit bir yinelemeli ifadeye dayanmaktadır:

Z = Z[i] * Z[i] + C,

burada Zi ve C karmaşık değişkenlerdir. Karmaşık düzlemin bir alt kümesi olan dikdörtgen veya kare bölgenin her başlangıç ​​noktası C için yinelemeler gerçekleştirilir. Yinelemeli süreç Z[i] merkezi (0,0) noktasında bulunan 2 yarıçaplı çemberin ötesine geçene kadar devam eder (bu, çekicinin dinamik sistem sonsuzdadır) veya yeterince sonra büyük sayı yinelemeler (örneğin 200-500) Z[i] çember üzerinde bir noktaya yakınlaşacaktır. Z[i]'nin daire içinde kaldığı yineleme sayısına bağlı olarak, C noktasının rengini ayarlayabilirsiniz (eğer Z[i] yeterince fazla sayıda yineleme boyunca dairenin içinde kalırsa, yineleme işlemi durur ve bu raster) nokta siyaha boyanmıştır).

Yukarıdaki algoritma Mandelbrot kümesi olarak adlandırılan kümeye bir yaklaşım verir. Mandelbrot kümesi şu noktaları içerir: sonsuz sayı yinelemeler sonsuza gitmez (noktalar siyahtır). Kümenin sınırına ait noktalar (bu, karmaşık yapılar) için sonsuza git son sayı yinelemeler ve kümenin dışında kalan noktalar birkaç yinelemeden sonra (beyaz arka plan) sonsuza gider.

Cebirsel fraktallara örnekler:

• Mandelbrot seti
• Julia setleri
• Halley fraktalı
• Newton'un fraktalı

Bu fraktali, bir nehrin yüzeyindeki dalgaların girişimine bakarken keşfettim. Dalga kıyıya doğru hareket eder, yansır ve kendi üzerine bindirilir. Dalgaların yarattığı desenlerde düzen var mı? Onu bulmaya çalışalım. Dalganın tamamını değil, yalnızca hareketinin vektörünü ele alalım. Deneyi basitleştirmek için "kıyıları" pürüzsüz hale getirelim.

Deney, okul not defterindeki normal bir kağıt parçası üzerinde gerçekleştirilebilir.

Veya algoritmanın JavaScript uygulamasını kullanarak.

Kenarları q ve p olan bir dikdörtgen alın. Köşeden köşeye bir ışın (vektör) gönderelim. Işın dikdörtgenin bir tarafına hareket eder, yansıtılır ve bir sonraki tarafa doğru hareket etmeye devam eder. Bu, ışın kalan köşelerden birine çarpana kadar devam eder. Eğer q ve p kenarlarının boyutları göreceli olarak asal sayılar ise, o zaman bir model elde edilir (daha sonra göreceğimiz gibi - bir fraktal).

Resimde bu algoritmanın nasıl çalıştığını açıkça görebiliyoruz.

Gif animasyonu:

En şaşırtıcı şey şu ki farklı taraflar dikdörtgen - farklı desenler elde ederiz.

Bu kalıplara neden fraktallar diyorum? Bildiğiniz gibi “fraktal” kendine benzerlik özelliği taşıyan geometrik bir şekildir. Resmin bir kısmı resmin tamamını tekrarlıyor. Q ve P kenarlarının boyutlarını önemli ölçüde artırırsanız, bu desenlerin kendine benzerlik özelliklerine sahip olduğu açıktır.

Bunu arttırmaya çalışalım. Bunu kurnazca artıracağız. Örnek olarak 17x29 modelini ele alalım. Aşağıdaki desenler şöyle olacaktır: 29x(17+29=46), 46x(29+46=75)…
Bir taraf: F(n);
İkinci taraf: F(n+1)=F(n)+F(n-1);
17, 29, 46, 75, 121, 196, 317, 513, 830, 1343
Fibonacci sayıları gibi, dizinin yalnızca birinci ve ikinci üyeleri farklı: F(0)=17, F(1)=29.

Eğer büyük taraf hatta sonuç şu modeldir:

Kısa kenar çift ise:

Her iki taraf da tek ise simetrik bir model elde ederiz:

Işının nasıl başladığına bağlı olarak:

veya

Bu dikdörtgenlerde neler olduğunu açıklamaya çalışacağım.

Kareyi dikdörtgenden ayıralım ve kenarda ne olacağını görelim.

Işın girdiği noktadan aynı yerden çıkar.

Aynı zamanda ışının içinden geçtiği karelerin sayısı da her zaman çift sayıdır.

Bu nedenle, bir dikdörtgenden bir kareyi keserseniz, fraktalın değişmeyen bir kısmı kalacaktır.

Kareleri fraktaldan olabildiğince çok ayırırsanız fraktalın "başlangıcına" ulaşabilirsiniz.

Fibonacci spiraline benziyor mu?

Fraktallar Fibonacci sayılarından da elde edilebilir.

Matematikte Fibonacci sayıları (Fibonacci serisi, Fibonacci dizisi) şu sayılardır:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597…
Tanım gereği, Fibonacci dizisindeki ilk iki sayı 0 ve 1'dir ve sonraki her sayı, önceki iki sayının toplamına eşittir.
F(n)=F(n-1)+F(n-2)
F(0)=0, F(1)=1

Hadi gidelim:

Görüldüğü gibi en-boy oranı altın orana yaklaştıkça fraktalın detayı da artıyor.

Bu durumda fraktal, fraktalın bir kısmını tekrarlayarak artar.

Fibonacci sayıları yerine irrasyonel kenar boyutlarını kullanabilirsiniz:

Aynı fraktalı elde ediyoruz.

Işını farklı bir açıyla çekerseniz aynı fraktallar bir karede elde edilebilir:

Sonuç olarak ne söyleyebilirsiniz?
Kaos aynı zamanda düzendir. Kendi kanunlarıyla. Bu düzen henüz incelenmemiştir, ancak çalışmaya oldukça uygundur. Ve bilimin tüm arzusu bu kalıpları keşfetmektir. Ve sonuçta büyük resmi görmek için yapbozun parçalarını birleştirin.
Nehrin yüzeyine bakalım. Ona taş atarsan dalgalar gelir. Çalışmaya oldukça uygun çevreler. Hız, periyot, dalga boyu – bunların hepsi hesaplanabilir. Ancak dalga kıyıya ulaşana kadar yansımaz ve kendi üzerine binmeye başlar. Zaten incelenmesi zor olan kaos (müdahale) elde ediyoruz.
Peki ya ters yönden hareket edersek? Dalganın davranışını mümkün olduğu kadar basitleştirin. Basitleştirin, bir model bulun ve ardından onu tanımlamaya çalışın tam resim neler oluyor?
Neler basitleştirilebilir? Açıkçası, yansıtıcı yüzeyi bükülmeden düz yapın. Daha sonra dalganın kendisi yerine yalnızca dalga hareket vektörünü kullanın. Prensip olarak bu, basit bir algoritma oluşturmak ve süreci bilgisayarda simüle etmek için yeterlidir. Ve sıradan bir kareli kağıt parçası üzerinde dalga davranışının bir "modelini" oluşturmak bile oldukça yeterlidir.
Sonuç olarak elimizde ne var? Sonuç olarak şunu görüyoruz. dalga süreçleri(nehrin yüzeyindeki aynı dalgalanmalar) elimizde kaos değil, üst üste binmiş fraktallar (kendine benzer yapılar) var.

Başka bir dalga türünü ele alalım. Bilindiği üzere elektromanyetik dalgaüç vektörden oluşur: dalga vektörü ve elektrik ve gerilim vektörü manyetik alan. Görebildiğimiz gibi, eğer böyle bir dalgayı "yakalarsanız" kapalı alan– bu vektörlerin kesiştiği yerde oldukça net kapalı yapılar elde ederiz. Belki temel parçacıklar– bunlar aynı fraktallar mı?

1'den 80'e kadar dikdörtgenlerdeki tüm fraktallar (6723x6723 piksel):

Fraktallarda kapalı alanlar (6723x6723 piksel):

Sadece güzel bir fraktal (4078x2518 piksel):