Başarılı bir şekilde çözmek için trigonometrik denklemler kullanımı uygun azaltma yöntemi Daha önce çözülmüş sorunlara. Bu yöntemin özünün ne olduğunu bulalım mı?
Önerilen herhangi bir görevde, önceden çözülmüş bir sorunu görmeniz ve ardından ardışık yöntemleri kullanarak eşdeğer dönüşümler Size verilen görevi daha basit hale getirmeye çalışın.
Yani karar verirken trigonometrik denklemler genellikle bir miktar tutar sonlu dizi son halkası açık çözümü olan bir denklem olan eşdeğer denklemler. Sadece en basit trigonometrik denklemleri çözme becerilerinin oluşmaması durumunda çözümün daha fazla olduğunu hatırlamak önemlidir. karmaşık denklemler zor ve etkisiz olacaktır.
Ayrıca trigonometrik denklemleri çözerken birden fazla olası çözüm yönteminin olduğunu asla unutmamalısınız.
Örnek 1. Kök sayısını bulun çünkü denklemler x = -1/2 aralığında.
Çözüm:
Yöntem I y = cos x ve y = -1/2 fonksiyonlarını çizelim ve aralıktaki ortak noktalarının sayısını bulalım (Şekil 1).
Fonksiyon grafiklerinde iki tane olduğundan ortak noktalar aralıkta ise denklem bu aralıkta iki kök içerir.
II yöntemi. Trigonometrik bir daire kullanarak (Şekil 2) noktaların sayısını buluyoruz aralığa ait, burada cos x = -1/2. Şekil denklemin iki kökü olduğunu göstermektedir. 
III yöntemi. Trigonometrik denklemin köklerine ilişkin formülü kullanarak cos x = -1/2 denklemini çözüyoruz.
x = ± arccos (-1/2) + 2πk, k – tam sayı (k € Z);
x = ± (π – arccos 1/2) + 2πk, k – tam sayı (k € Z);
x = ± (π – π/3) + 2πk, k – tam sayı (k € Z);
x = ± 2π/3 + 2πk, k – tam sayı (k € Z).
Aralık 2π/3 ve -2π/3 + 2π köklerini içerir; k bir tamsayıdır. Dolayısıyla denklemin belirli bir aralıkta iki kökü vardır.
Cevap: 2.
Gelecekte trigonometrik denklemler önerilen yöntemlerden biri kullanılarak çözülecek ve bu çoğu durumda diğer yöntemlerin kullanımını dışlamayacaktır.
Örnek 2. tg (x + π/4) = 1 denkleminin [-2π; 2π].
Çözüm:
Trigonometrik bir denklemin köklerine ilişkin formülü kullanarak şunu elde ederiz:
x + π/4 = arktan 1 + πk, k – tamsayı (k € Z);
x + π/4 = π/4 + πk, k – tam sayı (k € Z);
x = πk, k – tamsayı (k € Z);
Aralık [-2π; 2π] -2π sayılarına aittir; -π; 0; π; 2π. Yani denklemin belirli bir aralıkta beş kökü vardır.
Cevap: 5.
Örnek 3. Cos 2 x + sin x · cos x = 1 denkleminin [-π; π].
Çözüm:
1 = sin 2 x + cos 2 x olduğundan (temel trigonometrik özdeşlik), o zaman orijinal denklem şu şekli alır:
cos 2 x + sin x · cos x = sin 2 x + cos 2 x;
günah 2 x – sin x çünkü x = 0;
sin x(sin x – cos x) = 0. Çarpım sıfıra eşittir, bu da faktörlerden en az birinin şu şekilde olması gerektiği anlamına gelir: sıfıra eşit, Bu yüzden:
sin x = 0 veya sin x – çünkü x = 0.
cos x = 0 olan değişkenin değerleri ikinci denklemin kökleri olmadığından (aynı sayının sinüsü ve kosinüsü aynı anda sıfıra eşit olamaz), ikinci denklemin her iki tarafını da bölüyoruz çünkü x'e göre:
sin x = 0 veya sin x / cos x - 1 = 0.
İkinci denklemde tg x = sin x / cos x gerçeğini kullanırız, o zaman:
sin x = 0 veya tan x = 1. Formülleri kullanarak elimizde:
x = πk veya x = π/4 + πk, k – tam sayı (k € Z).
İlk kök serisinden [-π aralığına; π] -π sayılarına aittir; 0; π. İkinci seriden: (π/4 – π) ve π/4.
Yani beş kök var orijinal denklem[-π aralığına aittir; π].
Cevap: 5.
Örnek 4. [-π; aralığında tg 2 x + сtg 2 x + 3tg x + 3сtgx + 4 = 0 denkleminin köklerinin toplamını bulun. 1.1π].
Çözüm:
Denklemi şu şekilde yeniden yazalım:
tg 2 x + сtg 2 x + 3(tg x + сtgx) + 4 = 0 ve yerine koyma işlemini yapın.
tg x + сtgx = a olsun. Denklemin her iki tarafının karesini alalım:
(tg x + сtg x) 2 = a 2 . Parantezleri genişletelim:
tg 2 x + 2tg x · сtgx + сtg 2 x = a 2.
tg x · сtgx = 1 olduğundan, tg 2 x + 2 + сtg 2 x = a 2 olur, bunun anlamı
tg 2 x + сtg 2 x = a 2 – 2.
Şimdi orijinal denklem şuna benziyor:
a 2 – 2 + 3a + 4 = 0;
a 2 + 3a + 2 = 0. Vieta teoremini kullanarak a = -1 veya a = -2 olduğunu buluruz.
Ters yerine koyma işlemini yapalım, elimizde:
tg x + сtgx = -1 veya tg x + сtgx = -2. Ortaya çıkan denklemleri çözelim.
tg x + 1/tgx = -1 veya tg x + 1/tgx = -2.
İkisinin malına göre karşılıklıdırlar karşılıklı sayılar ilk denklemin köklerinin olmadığını belirleriz ve ikinci denklemden şunu elde ederiz:
tg x = -1, yani. x = -π/4 + πk, k – tam sayı (k € Z).
Aralık [-π; 1,1π] köklere aittir: -π/4; -π/4 + π. Toplamları:
-π/4 + (-π/4 + π) = -π/2 + π = π/2.
Cevap: π/2.
Örnek 5. Ortalamayı bulun aritmetik kökler günah denklemleri 3x + sin x = sin 2x [-π aralığında; 0,5π].
Çözüm:
Haydi yararlanalım formül günahıα + sin β = 2sin ((α + β)/2) çünkü ((α – β)/2), o zaman
sin 3x + sin x = 2sin ((3x + x)/2) cos ((3x – x)/2) = 2sin 2x cos x ve denklem şöyle olur:
2sin 2x çünkü x = sin 2x;
2sin 2x · cos x – sin 2x = 0. Çıkaralım ortak çarpan parantez dışında 2x günah
sin 2x(2cos x – 1) = 0. Ortaya çıkan denklemi çözün:
sin 2x = 0 veya 2cos x – 1 = 0; 
sin 2x = 0 veya cos x = 1/2;
2x = πk veya x = ±π/3 + 2πk, k – tam sayı (k € Z).
Böylece köklerimiz var
x = πk/2, x = π/3 + 2πk, x = -π/3 + 2πk, k – tam sayı (k € Z).
Aralık [-π; 0,5π] -π köklerine aittir; -π/2; 0; π/2 (ilk kök serisinden); π/3 (ikinci seriden); -π/3 (üçüncü seriden). Aritmetik ortalamaları:
(-π – π/2 + 0 + π/2 + π/3 – π/3)/6 = -π/6.
Cevap: -π/6.
Örnek 6. Sin x + cos x = 0 denkleminin [-1,25π; 2π].
Çözüm:
Bu denklem birinci dereceden homojen bir denklemdir. Her iki kısmını da cosx'e (kökü cos x = 0 olmayan değişkenin değeri) bölelim. verilen denklem, çünkü aynı sayının sinüsü ve kosinüsü aynı anda sıfıra eşit olamaz). Orijinal denklem:
x = -π/4 + πk, k – tam sayı (k € Z).
Aralık [-1,25π; 2π] -π/4 köklerine aittir; (-π/4 + π); ve (-π/4 + 2π).
Dolayısıyla verilen aralık denklemin üç kökünü içerir.
Cevap: 3.
En önemli şeyi yapmayı öğrenin - bir sorunu çözmek için net bir plan hayal edin, o zaman herhangi bir trigonometrik denklem elinizin altında olacaktır.
Hala sorularınız mı var? Trigonometrik denklemleri nasıl çözeceğinizi bilmiyor musunuz?
Bir öğretmenden yardım almak için kaydolun.
web sitesi, materyalin tamamını veya bir kısmını kopyalarken kaynağa bir bağlantı gereklidir.
Sipariş verebilirsiniz detaylı çözüm Senin görevin!!!
İşaretin altında bilinmeyeni içeren eşitlik trigonometrik fonksiyon("sin x, cos x, tan x" veya "ctg x") trigonometrik denklem olarak adlandırılır ve daha sonra bunların formüllerini ele alacağız.
En basit denklemler "sin x=a, cos x=a, tg x=a, ctg x=a"dır; burada "x" bulunacak açıdır, "a" ise herhangi bir sayıdır. Her birinin kök formüllerini yazalım.
1. Denklem 'sin x=a'.
`|a|>1` için çözümü yoktur.
Ne zaman `|a| \leq 1` var sonsuz sayı kararlar.
Kök formülü: `x=(-1)^n arcsin a + \pi n, n \in Z`
2. Denklem 'çünkü x=a'
`|a|>1` için - sinüs durumunda olduğu gibi, aralarındaki çözümler gerçek sayılar bulunmamaktadır.
Ne zaman `|a| \leq 1` var sonsuz küme kararlar.
Kök formülü: `x=\pm arccos a + 2\pi n, n \in Z`

Grafiklerde sinüs ve kosinüs için özel durumlar. 
3. Denklem 'tg x=a'
'a'nın herhangi bir değeri için sonsuz sayıda çözüme sahiptir.
Kök formülü: `x=arctg a + \pi n, n \in Z'

4. Denklem 'ctg x=a'
Ayrıca 'a'nın herhangi bir değeri için sonsuz sayıda çözüm vardır.
Kök formülü: `x=arcctg a + \pi n, n \in Z`

Tablodaki trigonometrik denklemlerin kökleri için formüller
Sinüs için:  Kosinüs için:
Kosinüs için:  Teğet ve kotanjant için:
Teğet ve kotanjant için:  Ters trigonometrik fonksiyonlar içeren denklemleri çözmek için formüller:
Ters trigonometrik fonksiyonlar içeren denklemleri çözmek için formüller:

Trigonometrik denklemleri çözme yöntemleri
Herhangi bir trigonometrik denklemin çözümü iki aşamadan oluşur:
- en basitine dönüştürmenin yardımıyla;
- Yukarıda yazılan kök formülleri ve tabloları kullanarak elde edilen en basit denklemi çözer.
Örnekler kullanarak ana çözüm yöntemlerine bakalım.
Cebirsel yöntem.
Bu yöntem, bir değişkeni değiştirmeyi ve onu bir eşitlikle değiştirmeyi içerir.
Örnek. Denklemi çözün: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 - x)+1=0`
`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,
değiştirmeyi yapın: `cos(x+\frac \pi 6)=y`, ardından `2y^2-3y+1=0`,
kökleri buluyoruz: `y_1=1, y_2=1/2`, bundan iki durum çıkıyor:
1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.
2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3- \frac \pi 6+2\pi n`.
Cevap: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Faktorizasyon.
Örnek. Denklemi çözün: 'sin x+cos x=1'.
Çözüm. Eşitliğin tüm terimlerini sola taşıyalım: `sin x+cos x-1=0`. kullanarak sol tarafı dönüştürür ve çarpanlara ayırırız:
'sin x — 2sin^2 x/2=0',
'2sin x/2 cos x/2-2sin^2 x/2=0',
'2sin x/2 (cos x/2-sin x/2)=0',
- "sin x/2 =0", "x/2 =\pi n", "x_1=2\pi n".
- `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n` , 'x_2=\pi/2+ 2\pi n'.
Cevap: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.
Homojen bir denkleme indirgeme
Öncelikle bu trigonometrik denklemi iki biçimden birine indirgemeniz gerekir:
`a günah x+b çünkü x=0` ( homojen denklem birinci derece) veya 'a sin^2 x + b sin x cos x +c cos^2 x=0' (ikinci derecenin homojen denklemi).
Daha sonra her iki parçayı da ilk durum için "cos x \ne 0"a, ikinci durum için "cos^2 x \ne 0"a bölün. Bilinen yöntemler kullanılarak çözülmesi gereken "tg x": "a tg x+b=0" ve "a tg^2 x + b tg x +c =0" denklemlerini elde ederiz.
Örnek. Denklemi çözün: "2 sin^2 x+sin x cos x - cos^2 x=1".
Çözüm. Haydi yazalım Sağ Taraf'1=sin^2 x+cos^2 x' gibi:
`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,
`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`
"sin^2 x+sin x cos x — 2 cos^2 x=0".
Bu ikinci dereceden homojen bir trigonometrik denklemdir, sol ve sağ taraflarını 'cos^2 x \ne 0'a bölersek şunu elde ederiz:
`\frac (sin^2 x)(cos^2 x)+\frac(sin x cos x)(cos^2 x) — \frac(2 cos^2 x)(cos^2 x)=0`
"tg^2 x+tg x — 2=0". Şimdi "t^2 + t - 2=0" sonucunu veren "tg x=t" yerine geçen ifadeyi tanıtalım. Bu denklemin kökleri "t_1=-2" ve "t_2=1"dir. Daha sonra:
- `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z'
- `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, ` n \in Z`.
Cevap. `x_1=arctg (-2)+\pi n`, `Z'de n \', `x_2=\pi/4+\pi n`, `Z'de n \'.
Yarım Açıya Geçiş
Örnek. Denklemi çözün: '11 sin x - 2 cos x = 10'.
Çözüm. Formülleri uygulayalım çift açı, sonuçta: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x/2+10 cos^ 2x/2`
`4 tg^2 x/2 — 11 tg x/2 +6=0`
Yukarıdakileri uygulamak cebirsel yöntem, şunu elde ederiz:
- `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
- `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Cevap. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Yardımcı açının tanıtılması
a,b,c'nin katsayılar ve x'in bir değişken olduğu "a sin x + b cos x =c" trigonometrik denkleminde, her iki tarafı da "sqrt (a^2+b^2)"'ye bölün:
`\frac a(sqrt (a^2+b^2)) sin x +` `\frac b(sqrt (a^2+b^2)) çünkü x =` `\frac c(sqrt (a^2) ) +b^2))'.
Sol taraftaki katsayılar sinüs ve kosinüs özelliğindedir yani karelerinin toplamı 1'e eşit ve modülleri 1'den büyük değildir. Bunları şu şekilde gösterelim: `\frac a(sqrt (a^2) +b^2))=cos \varphi` , ` \frac b(sqrt (a^2+b^2)) =sin \varphi`, `\frac c(sqrt (a^2+b^2)) =C`, o zaman:
`çünkü \varphi sin x + sin \varphi çünkü x =C`.
Aşağıdaki örneğe daha yakından bakalım:
Örnek. Denklemi çözün: '3 sin x+4 cos x=2'.
Çözüm. Eşitliğin her iki tarafını da "sqrt (3^2+4^2)"ye bölersek şunu elde ederiz:
`\frac (3 sin x) (sqrt (3^2+4^2))+` `\frac(4 cos x)(sqrt (3^2+4^2))=` `\frac 2(sqrt (3^2+4^2))'
'3/5 günah x+4/5 çünkü x=2/5'.
`3/5 = cos \varphi`, `4/5=sin \varphi` olsun. `sin \varphi>0`, `cos \varphi>0` olduğundan, o zaman yardımcı açı`\varphi=arcsin 4/5`'i alalım. Daha sonra eşitliğimizi şu şekilde yazıyoruz:
`çünkü \varphi sin x+sin \varphi çünkü x=2/5`
Sinüs açılarının toplamı formülünü uygulayarak eşitliğimizi aşağıdaki biçimde yazıyoruz:
'sin (x+\varphi)=2/5',
`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,
`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Cevap. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Kesirli rasyonel trigonometrik denklemler
Bunlar pay ve paydaları trigonometrik fonksiyonlar içeren kesirli eşitliklerdir.
Örnek. Denklemi çözün. `\frac (sin x)(1+cos x)=1-cos x`.
Çözüm. Eşitliğin sağ tarafını '(1+cos x)' ile çarpın ve bölün. Sonuç olarak şunu elde ederiz:
`\frac (sin x)(1+cos x)=` `\frac ((1-cos x)(1+cos x))(1+cos x)`
`\frac (sin x)(1+cos x)=` `\frac (1-cos^2 x)(1+cos x)`
`\frac (sin x)(1+cos x)=` `\frac (sin^2 x)(1+cos x)`
`\frac (sin x)(1+cos x)-` `\frac (sin^2 x)(1+cos x)=0`
`\frac (sin x-sin^2 x)(1+cos x)=0`
Paydanın sıfıra eşit olamayacağını düşünürsek, `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z` elde ederiz.
Kesrin payını sıfıra eşitleyelim: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Daha sonra "sin x=0" veya "1-sin x=0".
- `sin x=0`, `x=\pi n`, `Z'de n \`
- "1-sin x=0", "sin x=-1", "x=\pi /2+2\pi n, n \in Z".
` x \ne \pi+2\pi n, n \in Z` olduğu göz önüne alındığında, çözümler `x=2\pi n, n \in Z` ve `x=\pi /2+2\pi n` olur , 'n \ Z'de'.
Cevap. `x=2\pi n`, `Z'de n \`, `x=\pi /2+2\pi n`, `Z'de n \`.
Trigonometri ve özellikle trigonometrik denklemler geometri, fizik ve mühendisliğin hemen hemen tüm alanlarında kullanılmaktadır. Eğitim 10. sınıfta başlıyor, Birleşik Devlet Sınavı için her zaman görevler vardır, bu nedenle trigonometrik denklemlerin tüm formüllerini hatırlamaya çalışın - bunlar kesinlikle sizin için yararlı olacaktır!
Ancak bunları ezberlemenize bile gerek yok, asıl önemli olan özü anlamak ve onu çıkarabilmektir. Göründüğü kadar zor değil. Videoyu izleyerek kendiniz görün.
Basit trigonometrik denklemlerin çözümü.
Herhangi bir karmaşıklık düzeyindeki trigonometrik denklemlerin çözülmesi, sonuçta en basit trigonometrik denklemlerin çözülmesine indirgenir. Ve bunda en iyi yardımcı yine trigonometrik bir daire olduğu ortaya çıkıyor.
Kosinüs ve sinüs tanımlarını hatırlayalım.
Bir açının kosinüsü, üzerindeki bir noktanın apsisidir (yani eksen boyunca koordinattır). birim çember, belirli bir açı boyunca dönüşe karşılık gelir.
Bir açının sinüsü, belirli bir açı boyunca bir dönüşe karşılık gelen birim daire üzerindeki bir noktanın ordinatıdır (yani eksen boyunca koordinattır).
Boyunca pozitif hareket yönü trigonometrik daire Saat yönünün tersine hareket dikkate alınır. 0 derecelik (veya 0 radyan) bir dönüş, koordinatları (1;0) olan bir noktaya karşılık gelir
Bu tanımları basit trigonometrik denklemleri çözmek için kullanırız.
1. Denklemi çözün
Bu denklem, koordinatı eşit olan daire üzerindeki noktalara karşılık gelen dönme açısının tüm değerleri tarafından karşılanır.
Ordinat ekseninde ordinatı olan bir noktayı işaretleyelim:

Hadi gerçekleştirelim yatay çizgiçemberle kesişene kadar x eksenine paraleldir. Çember üzerinde uzanan ve ordinatı olan iki nokta elde ediyoruz. Bu noktalar, cinsinden dönme açılarına ve radyanlara karşılık gelir:

Radyanlarla dönme açısına karşılık gelen noktayı bırakarak etrafta dolaşırsak tam daire sonra radyan başına dönüş açısına karşılık gelen ve aynı koordinata sahip bir noktaya ulaşacağız. Yani bu dönme açısı da denklemimizi sağlıyor. Aynı noktaya dönerek istediğimiz kadar "boşta" dönüş yapabiliriz ve tüm bu açı değerleri denklemimizi karşılayacaktır. “Boşta” devirlerin sayısı (veya) harfiyle gösterilecektir. Bu devrimleri hem olumlu hem de olumsuz anlamda yapabildiğimiz için negatif yön, (veya ) herhangi bir tamsayı değerini alabilir.
Yani orijinal denklemin ilk çözüm serisi şu şekildedir:
![]() , , - tam sayılar kümesi (1)
, , - tam sayılar kümesi (1)
Benzer şekilde, ikinci çözüm serisi şu şekildedir:
![]() , Nerede , . (2)
, Nerede , . (2)
Tahmin edebileceğiniz gibi, bu çözüm serisi dairenin üzerindeki dönme açısına karşılık gelen noktaya dayanmaktadır.
Bu iki çözüm serisi tek bir girişte birleştirilebilir:
Bu girişi (yani eşit) alırsak, ilk çözüm serisini elde ederiz.
Bu girişi (yani tek) alırsak, ikinci çözüm serisini elde ederiz.
2. Şimdi denklemi çözelim
Bu, birim çember üzerindeki bir noktanın bir açıyla döndürülerek elde edilen apsisi olduğundan, eksen üzerinde apsis bulunan noktayı işaretleriz:

Hadi gerçekleştirelim dikey çizgi daireyle kesişene kadar eksene paraleldir. Çember üzerinde uzanan ve apsisi olan iki nokta elde edeceğiz. Bu noktalar dönme açılarına ve radyanlara karşılık gelir. Saat yönünde hareket ettiğimizde şunu elde ettiğimizi hatırlayın: negatif açı rotasyon:

İki dizi çözümü yazalım:
![]() ,
,
![]() ,
,
(Ana tam daireden yani yani daireden giderek istenilen noktaya ulaşıyoruz.
Bu iki seriyi tek bir girdide birleştirelim:
![]()
3. Denklemi çözün
Teğet doğru birim çemberin OY eksenine paralel (1,0) koordinatlı noktadan geçer
Üzerinde ordinatı 1'e eşit olan bir nokta işaretleyelim (açıları 1'e eşit olan teğetini arıyoruz):

Bu noktayı bir doğru ile koordinatların orijinine bağlayalım ve doğrunun birim çember ile kesişme noktalarını işaretleyelim. Düz çizgi ile dairenin kesişme noktaları ve üzerindeki dönme açılarına karşılık gelir:

Denklemimizi sağlayan dönme açılarına karşılık gelen noktalar birbirinden radyan uzaklıkta olduğundan çözümü şu şekilde yazabiliriz:
4. Denklemi çözün
Kotanjant çizgisi birim çemberin koordinatları eksene paralel olan noktadan geçer.
Kotanjantlar doğrusu üzerinde apsis -1 olan bir noktayı işaretleyelim:

Bu noktayı doğrunun başlangıç noktasına bağlayalım ve çemberle kesişene kadar devam edelim. Bu düz çizgi, daireyi dönme açılarına ve radyanlara karşılık gelen noktalarda kesecektir:

Bu noktalar birbirinden eşit mesafe ile ayrıldığından, o zaman ortak karar Bu denklemi şu şekilde yazabiliriz:
![]()
En basit trigonometrik denklemlerin çözümünü gösteren verilen örneklerde, trigonometrik fonksiyonların tablo değerleri kullanılmıştır.
Ancak denklemin sağ tarafında hiçbir şey yoksa tablo değeri sonra değeri denklemin genel çözümüne koyarız:




ÖZEL ÇÖZÜMLER:
Ordinatı 0 olan çember üzerinde noktaları işaretleyelim:

Ordinatı 1 olan çember üzerinde tek bir noktayı işaretleyelim:

Çember üzerinde koordinatı -1 olan tek bir noktayı işaretleyelim:

Sıfıra en yakın değerleri belirtmek alışılmış olduğundan çözümü şu şekilde yazıyoruz:
Apsisi 0’a eşit olan çember üzerinde noktaları işaretleyelim:

5.
Apsisi 1’e eşit olan çember üzerinde tek bir nokta işaretleyelim:

Apsisi -1 olan çember üzerinde tek bir nokta işaretleyelim:

Ve biraz daha karmaşık örnekler:
1.
Sinüs bire eşit eğer argüman eşitse
Sinüsümüzün argümanı eşittir, dolayısıyla şunu elde ederiz:
Eşitliğin her iki tarafını da 3'e bölelim:
Cevap:
2.
Kosinüs argümanı ise kosinüs sıfırdır
Kosinüsümüzün argümanı eşittir ve şunu elde ederiz:
İfade edelim, bunun için önce ters işaretle sağa doğru hareket edelim:
Sağ tarafı sadeleştirelim:
Her iki tarafı da -2'ye bölün:
K herhangi bir tamsayı değeri alabildiğinden, terimin önündeki işaretin değişmediğine dikkat edin.
Cevap:
Ve son olarak “Trigonometrik bir denklemde köklerin seçilmesi” başlıklı video eğitimini izleyin. trigonometrik daire"
Böylece basit trigonometrik denklemlerin çözümü hakkındaki konuşmamız sona eriyor. Bir dahaki sefere nasıl karar vereceğimizi konuşacağız.
Trigonometrik denklemler. Matematik sınavının ilk bölümünde denklem çözme ile ilgili bir görev bulunmaktadır. basit denklemler Dakikalar içerisinde çözülen bu sorunun birçok türü ağız yoluyla çözülebilmektedir. İçerir: doğrusal, ikinci dereceden, rasyonel, irrasyonel, üstel, logaritmik ve trigonometrik denklemler.
Bu yazıda trigonometrik denklemlere bakacağız. Çözümleri hem hesaplama hacmi hem de karmaşıklık açısından bu bölümdeki diğer problemlerden farklıdır. Paniğe kapılmayın, "zorluk" kelimesi diğer görevlere kıyasla göreceli zorluklarını ifade eder.
Denklemin köklerini bulmanın yanı sıra, en büyük negatifi veya en küçük olanı belirlemek de gereklidir. pozitif kök. Sınavda trigonometrik bir denklem elde etme olasılığınız elbette düşüktür.
Birleşik Devlet Sınavının bu bölümünde bunların% 7'sinden azı var. Ancak bu onların göz ardı edilmesi gerektiği anlamına gelmez. Bölüm C'de ayrıca bir trigonometrik denklemi çözmeniz gerekir, dolayısıyla çözüm tekniğini ve teoriyi iyi anlamak kesinlikle gereklidir.
Matematiğin trigonometri bölümünü anlamak, birçok problemi çözmedeki başarınızı büyük ölçüde belirleyecektir. Cevabın bir tam sayı veya sonlu bir sayı olduğunu hatırlatırım ondalık. Denklemin köklerini aldıktan sonra kontrol ettiğinizden emin olun. Fazla zaman almayacak ve sizi hata yapmaktan kurtaracaktır.
İleride diğer denklemlere de bakacağız, kaçırmayın! Trigonometrik denklemlerin köklerine ilişkin formülleri hatırlayalım, bunları bilmeniz gerekir:

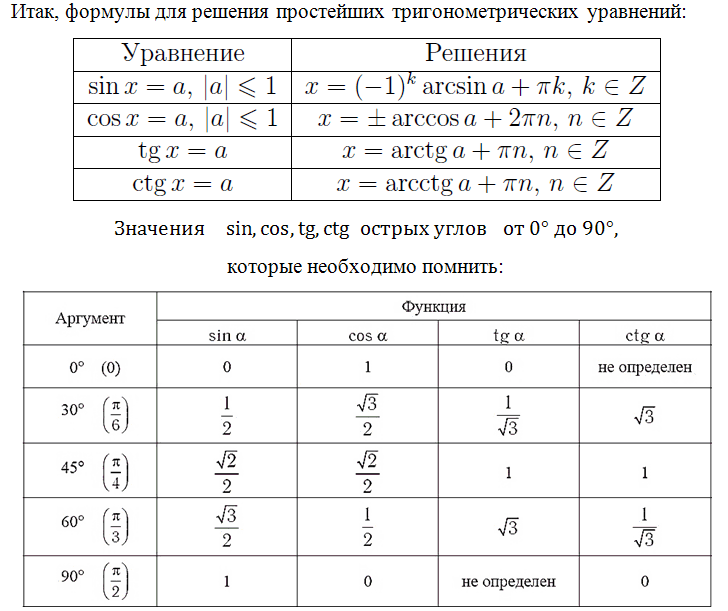
Bu değerlerin bilgisi gereklidir; bu, birçok görevle baş etmenin imkansız olacağı “ABC” dir. Harika, eğer hafızanız iyiyse bu değerleri kolaylıkla öğrenmiş ve hatırlamışsınızdır. Bunu yapamıyorsanız ne yapmalısınız, kafanızda bir karmaşa var ama sınava girerken kafanız karıştı. Hesaplamalarınızda yanlış değeri yazdığınız için puan kaybetmek yazık olur.
Bu değerler basittir, bültene abone olduktan sonra aldığınız ikinci mektupta aldığınız teoride de verilmiştir. Henüz abone olmadıysanız mutlaka yapın! İleride bu değerlerin trigonometrik çemberden nasıl belirlenebileceğine de bakacağız. Ona "Trigonometrinin Altın Kalbi" denmesi boşuna değil.
Karışıklığı önlemek için hemen açıklayayım, aşağıda ele alınan denklemlerde açı kullanılarak ark sinüs, ark kosinüs, ark tanjant tanımları verilmiştir. X karşılık gelen denklemler için: cosx=a, sinx=a, tgx=a, burada X bir ifade de olabilir. Aşağıdaki örneklerde argümanımız tam olarak bir ifadeyle belirtilmiştir.
Öyleyse aşağıdaki görevleri ele alalım:
Denklemin kökünü bulun:

Cevabınızdaki en büyük negatif kökü yazın.
Cos x = a denkleminin çözümü iki köktür:

Tanım: a sayısının modülü bir'i geçmeyen olsun. Bir sayının ark kosinüsü, kosinüsü a'ya eşit olan 0 ila Pi aralığında yer alan x açısıdır.

Araç

Hadi ifade edelim X:

En büyük negatif kökü bulalım. Nasıl yapılır? Hadi değiştirelim Farklı anlamlar Ortaya çıkan köklere n ekleyin, en büyük negatif olanı hesaplayın ve seçin.
Hesaplıyoruz:
n = – 2 x 1 = 3 (– 2) – 4,5 = – 10,5 x 2 = 3 (– 2) – 5,5 = – 11,5
n = – 1 x 1 = 3 (– 1) – 4,5 = – 7,5 x 2 = 3 (– 1) – 5,5 = – 8,5
n = 0 x 1 = 3∙0 – 4,5 = – 4,5 x 2 = 3∙0 – 5,5 = – 5,5 ile
n = 1 x 1 = 3∙1 – 4,5 = – 1,5 x 2 = 3∙1 – 5,5 = – 2,5 ile
n = 2 x 1 = 3∙2 – 4,5 = 1,5 x 2 = 3∙2 – 5,5 = 0,5 ile
En büyük negatif kökün –1,5 olduğunu bulduk
Cevap: –1.5
Kendin için karar ver:

Denklemi çözün:

Sin x = a denkleminin çözümü iki köktür:

Ya (yukarıdakilerin her ikisini de birleştirir):

Tanım: Modüldeki a sayısı bir'i aşmasın. Bir sayının ark sinüsü –90° ila 90° aralığında yer alan ve sinüsü a'ya eşit olan x açısıdır.

Araç

x'i ifade edin (denklemin her iki tarafını 4 ile çarpın ve Pi'ye bölün):

En küçük pozitif kökü bulalım. Burada ikame sırasında hemen anlaşılıyor negatif değerler n alacağız negatif kökler. Bu nedenle n = 0,1,2'yi yerine koyacağız...
n = 0 olduğunda x = (– 1) 0 + 4∙0 + 3 = 4
n = 1 olduğunda x = (– 1) 1 + 4∙1 + 3 = 6
n = 2 ile x = (– 1) 2 + 4∙2 + 3 = 12
n = –1 x = (–1) –1 + 4∙(–1) + 3 = –2 ile kontrol edelim.
Yani en küçük pozitif kök 4'tür.
Cevap: 4
Kendin için karar ver:

Denklemi çözün:

Cevabınızdaki en küçük pozitif kökü yazın.








