1 apibrėžimas. Skaičių ašis (skaičių eilutė, koordinačių eilutė) Ox yra tiesi linija, kurioje pasirinktas taškas O kilmė (koordinačių pradžia)(1 pav.), kryptis

O → x

išvardyti kaip teigiama kryptimi ir pažymimas atkarpa, kurios ilgis laikomas ilgio vienetas.

2 apibrėžimas. Atkarpa, kurios ilgis laikomas ilgio vienetu, vadinamas masteliu.

Kiekvienas skaičių ašies taškas turi koordinatę, kuri yra tikras numeris. Taško O koordinatė lygi nuliui. Savavališko taško A, gulinčio ant spindulio Ox, koordinatė lygi atkarpos OA ilgiui.

Savavališko skaitinės ašies taško A, kuris nėra ant spindulio Ox, koordinatė yra neigiama ir absoliučia reikšme lygi atkarpos OA ilgiui. 3 apibrėžimas. Stačiakampė Dekarto koordinačių sistema Oxy plokštumoje skambinkite abiem statmenai skaitinės ašys Ox ir Oy su ta pati skalė Ir bendra pradžia atgalinis skaičiavimas taške O ir taip, kad sukimasis nuo spindulio Ox 90° kampu į spindulį Oy būtų vykdomas kryptimi prieš laikrodžio rodyklę

(2 pav.). Pastaba. Stačiakampė Dekarto koordinačių sistema Oxy, parodyta 2 paveiksle, vadinama teisinga koordinačių sistema , Skirtingai nei kairiosios koordinačių sistemos , kuriame sijos Ox sukimas 90° kampu į siją Oy atliekamas pagal laikrodžio rodyklę. Šiame vadove mes laikome tik dešiniarankes koordinačių sistemas

, konkrečiai to nenurodant. Jei plokštumoje įvesime kokią nors stačiakampių Dekarto koordinačių sistemą Oxy, tai kiekvienas plokštumos taškas įgis – dvi koordinates ta pati skalė abscisė ordinatės , kurios apskaičiuojamos taip. Tegu A yra savavališkas plokštumos taškas. Iš taško A numeskime statmenis A.A. , kurios apskaičiuojamos taip. Tegu A yra savavališkas plokštumos taškas. Iš taško A numeskime statmenis 1 ir

2 į tiesias linijas Ox ir Oy, atitinkamai (3 pav.). 4 apibrėžimas. Taško A abscisė yra taško koordinatė A 4 apibrėžimas. Taško A abscisė yra taško koordinatė 1 skaičių ašyje Ox, taško A ordinatė yra taško koordinatė

2 skaičių ašyje Oy. Paskyrimas Taško koordinatės (abscisės ir ordinatės). A stačiakampyje Dekarto sistema 4 apibrėžimas. Taško A abscisė yra taško koordinatė(x;Dažniausiai žymimos deguonies koordinatės (4 pav.).) y 4 apibrėžimas. Taško A abscisė yra taško koordinatė = (x; arba).

y Pastaba. Taškas O, vadinamas kilmės O(0 ; 0) .

5 apibrėžimas. Stačiakampėje Dekarto koordinačių sistemoje Oxy skaičių ašis Ox vadinama abscisių ašimi, o skaitinė ašis Oy – ordinačių ašimi (5 pav.).

6 apibrėžimas. Kiekviena stačiakampė Dekarto koordinačių sistema padalija plokštumą į 4 ketvirčius (kvadrantus), kurių numeracija parodyta 5 pav.

7 apibrėžimas. Plokštuma, kurioje pateikta stačiakampė Dekarto koordinačių sistema, vadinama koordinačių plokštuma.

Pastaba. Nustatyta abscisių ašis koordinačių plokštuma lygtis arba= 0, ordinačių ašis koordinačių plokštumoje nurodoma lygtimi x = 0.

1 teiginys. Atstumas tarp dviejų taškų koordinačių plokštuma

4 apibrėžimas. Taško A abscisė yra taško koordinatė 1 (x 1 ;Dažniausiai žymimos deguonies koordinatės (4 pav.). 1) ta pati skalė 4 apibrėžimas. Taško A abscisė yra taško koordinatė 2 (x 2 ;Dažniausiai žymimos deguonies koordinatės (4 pav.). 2)

apskaičiuotas pagal formulę

Įrodymas . Apsvarstykite 6 pav.

Vadinasi,

Q.E.D.

Koordinačių plokštumos apskritimo lygtis

Nagrinėkime koordinačių plokštumoje Oxy (7 pav.) R spindulio apskritimą, kurio centras yra taške 4 apibrėžimas. Taško A abscisė yra taško koordinatė 0 (x 0 ;Dažniausiai žymimos deguonies koordinatės (4 pav.). 0) .

Stačiakampę koordinačių sistemą plokštumoje sudaro dvi viena kitai statmenos koordinačių ašys X’X ir Y’Y. Koordinačių ašys susikerta taške O, kuris vadinamas pradžios tašku, kiekvienoje ašyje parenkama teigiama kryptis. Teigiama ašių kryptis (dešiniojoje koordinačių sistemoje) parenkama taip, kad pasukus X'X ašį. prieš laikrodžio rodyklę 90°, jo teigiama kryptis sutampa su Y'Y ašies teigiama kryptimi. Keturi kampai (I, II, III, IV), sudaryti iš koordinačių ašių X'X ir Y'Y, vadinami koordinačių kampais (žr. 1 pav.).

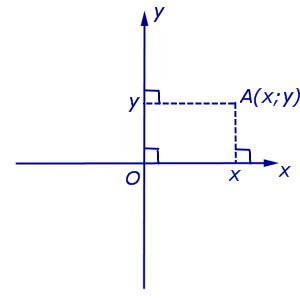
Taško A padėtis plokštumoje nustatoma pagal dvi koordinates x ir y. X koordinatė lygi atkarpos OB ilgiui, y koordinatė lygi atkarpos OC ilgiui pasirinktuose matavimo vienetuose. Atkarpas OB ir OC apibrėžia linijos, nubrėžtos iš taško A, lygiagrečios Y'Y ir X'X ašims, atitinkamai. Koordinatė x vadinama taško A abscise, y – taško A ordinate. Rašoma taip: A(x, y).

Jei taškas A yra koordinačių kampas I, tada taškas A turi teigiamą abscisę ir ordinatę. Jei taškas A yra koordinačių kampe II, tai taškas A turi neigiamą abscisę ir teigiamą ordinatę. Jei taškas A yra koordinačių kampe III, tai taškas A turi neigiamą abscisę ir ordinatę. Jei taškas A yra IV koordinačių kampe, tai taškas A turi teigiamą abscisę ir neigiamą ordinatę.

Stačiakampė koordinačių sistema erdvėje sudaro trys viena kitai statmenos koordinačių ašys OX, OY ir OZ. Koordinačių ašys susikerta taške O, kuris vadinamas pradiniu tašku, ant kiekvienos ašies pasirenkama teigiama kryptis, pažymėta rodyklėmis, ir atkarpų ant ašių matavimo vienetas. Matavimo vienetai yra vienodi visoms ašims. OX - abscisių ašis, OY - ordinačių ašis, OZ - taikymo ašis. Teigiama ašių kryptis parenkama taip, kad OX ašį pasukus prieš laikrodžio rodyklę 90°, jos teigiama kryptis sutaptų su teigiama OY ašies kryptimi, jei šis sukimasis stebimas iš teigiamos OZ ašies krypties. Tokia koordinačių sistema vadinama dešiniaranke. Jeigu nykštys dešinė ranka imkime X kryptį kaip X kryptį, indeksinę – kaip Y kryptį, o vidurinę – kaip Z kryptį, tada susidaro dešinioji koordinačių sistema. Panašūs kairės rankos pirštai sudaro kairiąją koordinačių sistemą. Neįmanoma sujungti dešinės ir kairės koordinačių sistemų taip, kad atitinkamos ašys sutaptų (žr. 2 pav.).

Taško A padėtis erdvėje nustatoma pagal tris koordinates x, y ir z. Koordinatė x lygi atkarpos OB ilgiui, y koordinatė – atkarpos OC ilgiui, z koordinatė – atkarpos OD ilgiui pasirinktais matavimo vienetais. Atkarpas OB, OC ir OD apibrėžia plokštumos, nubrėžtos iš taško A, lygiagrečios atitinkamai plokštumoms YOZ, XOZ ir XOY. Koordinatė x vadinama taško A abscise, y koordinatė vadinama taško A ordinate, z koordinatė vadinama taško A aplikacija. Rašoma taip: A(a, b, c).

Orty

Stačiakampė koordinačių sistema (bet kokio matmens) taip pat apibūdinama vienetų vektorių rinkiniu, sulygiuotu su koordinačių ašimis. Vienetų vektorių skaičius yra lygus koordinačių sistemos matmeniui ir visi jie yra statmeni vienas kitam.

Trimačiu atveju tokie vienetiniai vektoriai dažniausiai žymimi i j k y e x e y e z. Be to, tuo atveju teisinga sistema galioja koordinatės sekančias formules su vektorių kryžmine sandauga:

• [i j]=k ;
• [j k]=i ;
• [k i]=j .

Istorija

Stačiakampę koordinačių sistemą pirmą kartą pristatė Rene'as Descartes'as savo darbe „Metodo diskursas“ 1637 m. Todėl stačiakampė koordinačių sistema taip pat vadinama - Dekarto koordinačių sistema. Geometrinių objektų apibūdinimo koordinačių metodas padėjo pagrindą analitinė geometrija. Pierre'as Fermatas taip pat prisidėjo prie koordinačių metodo kūrimo, tačiau jo darbai pirmą kartą buvo paskelbti po jo mirties. Dekartas ir Ferma koordinačių metodą naudojo tik plokštumoje.

Koordinačių metodas trimatė erdvė pirmą kartą panaudojo Leonhardas Euleris XVIII a.

taip pat žr

Nuorodos

Wikimedia fondas.

• Dekarto koordinačių sistema
• Dekarto laipsnis

Pažiūrėkite, kas yra „Dekarto koordinatės“ kituose žodynuose:

KARTESINOS KOORDINATES- (Dekarto koordinačių sistema) koordinačių sistema plokštumoje arba erdvėje, paprastai su viena kitai statmenomis ašimis ir lygiomis mastelėmis išilgai stačiakampių ašių Dekarto koordinatės. R. Dekarto vardu pavadintas... Didysis enciklopedinis žodynas

Dekarto koordinatės- Koordinačių sistema, susidedanti iš dviejų statmenų ašių. Taško padėtis tokioje sistemoje formuojama naudojant du skaičius, kurie nustato atstumą nuo koordinačių centro išilgai kiekvienos ašies. Informacinės temos......

Dekarto koordinatės Techninis vertėjo vadovas - (Dekarto koordinačių sistema), koordinačių sistema plokštumoje arba erdvėje, dažniausiai su viena kitai statmenomis ašimis ir vienodomis mastelėmis išilgai stačiakampių stačiakampių koordinačių. R. Dekarto vardu pavadintas...

Dekarto koordinatės enciklopedinis žodynas - Dekarto koordinatės statusas T sritis Standartizacija ir metrologija apibrėžtis Tiesinė plokštumos arba erdvės koordinačių sistema. Joje ašių masteliai paprastai būna lygūs. atitikmenys: angl. Dekarto koordinatės vok. kartesische Koordinaten, f…

Dekarto koordinatės Penkiakalbis aiškinamasis metrologijos terminų žodynas

KARTESINOS KOORDINATES- Dekarto koordinatės statusas T sritis fizika atitikmenys: engl. Dekarto koordinatės; tinklelio koordinatės vok. kartesische Koordinaten, f rus. Dekarto koordinatės, f pranc. coordonnées cartésiennes, f … Fizikos terminų žodynas - taškų padėties plokštumoje nustatymo pagal atstumą iki dviejų fiksuotų statmenų tiesių ašių metodas. Ši sąvoka jau matoma Archimede ir Pergos Apologise daugiau nei prieš du tūkstančius metų ir net tarp senovės egiptiečių. Pirmą kartą ši......

KARTESINOS KOORDINATES Matematinė enciklopedija - Dekarto koordinačių sistema [pavadinta prancūzų vardu. filosofas ir matematikas R. Dekartas (R. Dekartas; 1596 1650)], koordinačių sistema plokštumoje arba erdvėje, paprastai su viena kitai statmenomis ašimis ir lygiomis mastelėmis išilgai ašių stačiakampio D ...

KARTESINOS KOORDINATES Didysis enciklopedinis politechnikos žodynas - (Dekarto koordinačių sistema), koordinačių sistema plokštumoje arba erdvėje, dažniausiai su viena kitai statmenomis ašimis ir lygiomis mastelėmis išilgai stačiakampių ašių Pavadinta R. Dekarto vardu...

KARTESINOS KOORDINATES Gamtos mokslai. enciklopedinis žodynas - Sistema, skirta bet kurio taško, esančio ant kaulų, padėties dviejų ašių, susikertančių stačiu kampu, atžvilgiu. Ši sistema, kurią sukūrė René Descartes, tapo pagrindu standartiniai metodai grafinis vaizdavimas Horizontali linija… … Žodynas psichologijoje

Koordinatės- Koordinatės. Plokštumoje (kairėje) ir erdvėje (dešinėje). KOORDINATES (iš lotynų co kartu ir ordinatus ordered), skaičiai, nustatantys taško padėtį tiesėje, plokštumoje, paviršiuje, erdvėje. Koordinatės yra atstumai... Iliustruotas enciklopedinis žodynas

Instrukcijos

Užsirašyti matematines operacijas teksto forma ir įveskite juos į paieškos užklausos lauką adresu pagrindinis puslapis Google svetainę, jei negalite naudotis skaičiuokle, bet turite prieigą prie interneto. Šioje paieškos sistemoje yra įmontuotas daugiafunkcis skaičiuotuvas, kuriuo naudotis daug lengviau nei bet kuriuo kitu. Nėra sąsajos su mygtukais – visi duomenys turi būti įvesti teksto forma viename lauke. Pavyzdžiui, jei žinoma koordinates ekstremalūs taškai segmentas trimatėje koordinačių sistemoje A(51,34 17,2 13,02) ir A(-11,82 7,46 33,5), tada koordinates vidurio taškas segmentas C((51.34-11.82)/2 (17.2+7.46)/2 (13.02+33.5)/2). Į paieškos užklausos lauką įvedę (51.34-11.82)/2, tada (17.2+7.46)/2 ir (13.02+33.5)/2, galite naudoti Google, kad gautumėte koordinates C(19,76 12,33 23,26).

Standartinė lygtis ratas leidžia sužinoti keletą svarbi informacija apie šią figūrą, pavyzdžiui, jos centro koordinates, spindulio ilgį. Kai kuriose problemose, atvirkščiai, duotus parametrus reikia sukurti lygtį.

Instrukcijos

Pagal jums duotą užduotį nustatykite, kokią informaciją turite apie ratą. Prisiminti, kad Pagrindinis tikslas yra poreikis nustatyti centro koordinates, taip pat skersmenį. Visi jūsų veiksmai turėtų būti nukreipti į šį konkretų rezultatą.

Naudokite duomenis apie susikirtimo su koordinačių linijomis ar kitomis linijomis taškus. Atkreipkite dėmesį, kad jei apskritimas eina per abscisių ašį, antrosios koordinatės bus 0, o jei eina per ordinačių ašį, tada pirmoji. Šios koordinatės leis jums rasti apskritimo centro koordinates ir taip pat apskaičiuoti spindulį.

Nepamirškite apie pagrindines sekantų ir tangentų savybes. Visų pirma, naudingiausia teorema yra ta, kad kontakto taške spindulys ir liestinė sudaro stačią kampą. Tačiau atkreipkite dėmesį, kad jūsų gali būti paprašyta įrodyti visas kurso metu naudotas teoremas.

Išspręskite standartinius tipus, kad išmoktumėte iš karto pamatyti, kaip naudoti tam tikrus duomenis apskritimo lygtims. Taigi, be jau minėtų užduočių su tiesiogiai nurodytos koordinatės ir tie, kuriuose pateikiama informacija apie susikirtimo taškų buvimą, norėdami sudaryti apskritimo lygtį, galite naudoti žinias apie apskritimo centrą, stygos ilgį ir ant kurio yra ši styga.

Spręsti, konstruoti lygiašonis trikampis, kurio pagrindas bus duotas akordas, A lygios pusės– spinduliai. Kompiliavimas, iš kurio lengvai rasite reikiamus duomenis. Norėdami tai padaryti, pakanka naudoti atkarpos ilgio plokštumoje nustatymo formulę.

Video tema

Apskritimas suprantamas kaip figūra, susidedanti iš daugelio taškų plokštumoje, nutolusioje nuo jo centro vienodu atstumu. Atstumas nuo centro iki taškų ratas vadinamas spinduliu.

Dviejų ar trijų susikertančių, viena kitai statmenų ašių, turinčių bendrą pradžią (koordinačių pradžią) ir bendrą ilgio vienetą, sistema vadinama stačiakampė Dekarto koordinačių sistema .

Bendroji Dekarto koordinačių sistema (afininė koordinačių sistema) nebūtinai gali apimti statmenas ašis. garbei prancūzų matematikas Renė Dekartas (1596-1662) įvardijo kaip tik tokią koordinačių sistemą, kurioje visose ašyse matuojamas bendras ilgio vienetas, o ašys yra tiesios.

Stačiakampė Dekarto koordinačių sistema plokštumoje turi dvi ašis ir stačiakampė Dekarto koordinačių sistema erdvėje - trys ašys. Kiekvienas taškas plokštumoje arba erdvėje apibrėžiamas sutvarkyta koordinačių rinkiniu – skaičiais, atitinkančiais koordinačių sistemos ilgio vienetą.

Atkreipkite dėmesį, kad, kaip matyti iš apibrėžimo, Dekarto koordinačių sistema yra tiesioje linijoje, ty vienoje dimensijoje. Dekarto koordinačių įvedimas tiesėje yra vienas iš būdų, kaip bet kuris linijos taškas susiejamas su tiksliai apibrėžtu realiuoju skaičiumi, ty koordinate.

Rene Descartes'o darbuose atsiradęs koordinačių metodas žymėjo revoliucinį visos matematikos pertvarkymą. Pasidarė įmanoma interpretuoti algebrines lygtis(arba nelygybes) geometrinių vaizdų (grafikų) pavidalu ir, atvirkščiai, ieškoti sprendimo geometrinės problemos naudojant analitines formules ir lygčių sistemas. Taip, nelygybė z < 3 геометрически означает полупространство, лежащее ниже плоскости, параллельной координатной плоскости xOy ir esantis virš šios plokštumos 3 vnt.

Naudojant Dekarto koordinačių sistemą, taško priklausomybė duotoje kreivėje atitinka tai, kad skaičiai x ta pati skalė arba patenkinti kokią nors lygtį. Taigi apskritimo taško, kurio centras yra nurodytame taške, koordinatės ( a; b) tenkina lygtį (x - a)² + ( arba - b)² = R² .

Stačiakampė Dekarto koordinačių sistema plokštumoje

Plokštumoje susidaro dvi statmenos ašys, turinčios bendrą pradžią ir tą patį mastelio vienetą Dekarto stačiakampio koordinačių sistema plokštumoje . Viena iš šių ašių vadinama ašimi Jautis, arba x ašis , kita - ašis Oy, arba y ašis . Šios ašys taip pat vadinamos koordinačių ašimis. Pažymėkime pagal Mx Ir My atitinkamai savavališko taško projekcija M ant ašies Jautis Ir Oy. Kaip gauti prognozes? Pereikime per tašką M Jautis. Ši tiesi linija kerta ašį Jautis taške Mx. Pereikime per tašką M tiesi linija, statmena ašiai Oy. Ši tiesi linija kerta ašį Oy taške My. Tai parodyta paveikslėlyje žemiau.

x Ir arba taškų M atitinkamai pavadinsime nukreiptų segmentų reikšmes OMx Ir OMy. Šių nukreiptų segmentų vertės apskaičiuojamos atitinkamai kaip x = x0 - 0 Ir arba = arba0 - 0 . Dekarto koordinatės x Ir arba taškų M abscisė ta pati skalė ordinatės . Faktas, kad taškas M turi koordinates x Ir arba, žymimas taip: M(x, arba) .

Koordinačių ašys padalija plokštumą į keturias kvadrantas , kurių numeracija parodyta paveikslėlyje žemiau. Tai taip pat rodo taškų koordinačių ženklų išdėstymą, atsižvelgiant į jų vietą tam tikrame kvadrante.

Be Dekarto stačiakampių koordinačių plokštumoje, dažnai atsižvelgiama ir į polinių koordinačių sistemą. Apie perėjimo iš vienos koordinačių sistemos į kitą būdą – pamokoje poliarinė koordinačių sistema .

Stačiakampė Dekarto koordinačių sistema erdvėje

Dekarto koordinatės erdvėje įvedamos visiškai analogiškai su Dekarto koordinatėmis plokštumoje.

Trys viena kitai statmenos ašys erdvėje ( koordinačių ašys) su bendra pradžia O ir su tuo pačiu mastelio vienetu jie sudaro Dekarto stačiakampė koordinačių sistema erdvėje .

Viena iš šių ašių vadinama ašimi Jautis, arba x ašis , kita - ašis Oy, arba y ašis , trečioji – ašis Ozas, arba ašis taikyti . Leisti Mx, My Mz- savavališko taško projekcijos M erdvė ant ašies Jautis , Oy Ir Ozas atitinkamai.

Pereikime per tašką M JautisJautis taške Mx. Pereikime per tašką M plokštuma, statmena ašiai Oy. Ši plokštuma kerta ašį Oy taške My. Pereikime per tašką M plokštuma, statmena ašiai Ozas. Ši plokštuma kerta ašį Ozas taške Mz.

Dekarto stačiakampės koordinatės x , arba Ir z taškų M atitinkamai pavadinsime nukreiptų segmentų reikšmes OMx, OMy ta pati skalė OMz. Šių nukreiptų segmentų vertės apskaičiuojamos atitinkamai kaip x = x0 - 0 , arba = arba0 - 0 Ir z = z0 - 0 .

Dekarto koordinatės x , arba Ir z taškų M atitinkamai vadinami abscisė , ordinatės ta pati skalė kreiptis .

Koordinačių ašys, paimtos poromis, yra koordinačių plokštumose xOy , yOz Ir zOx .

Dekarto koordinačių sistemos taškų uždaviniai

1 pavyzdys.

4 apibrėžimas. Taško A abscisė yra taško koordinatė(2; -3) ;

B(3; -1) ;

C(-5; 1) .

Raskite šių taškų projekcijų į abscisių ašį koordinates.

Sprendimas. Kaip matyti iš teorinės šios pamokos dalies, taško projekcija į abscisių ašį yra pačioje abscisių ašyje, ty ašyje Jautis, todėl turi abscisę, lygią paties taško abscisei, ir ordinatę (ašies koordinatę Oy, kurią x ašis kerta taške 0), lygus nuliui. Taigi gauname šias x ašies taškų koordinates:

4 apibrėžimas. Taško A abscisė yra taško koordinatėx(2;0);

Bx(3;0);

Cx (-5; 0).

2 pavyzdys. Dekarto koordinačių sistemoje taškai pateikiami plokštumoje

4 apibrėžimas. Taško A abscisė yra taško koordinatė(-3; 2) ;

B(-5; 1) ;

C(3; -2) .

Raskite šių taškų projekcijų koordinates į ordinačių ašį.

Sprendimas. Kaip matyti iš šios pamokos teorinės dalies, taško projekcija į ordinačių ašį yra pačioje ordinačių ašyje, ty ašyje Oy, todėl turi ordinatę, lygią paties taško ordinatėms, ir abscisę (ašies koordinatę Jautis, kurią ordinačių ašis kerta taške 0), kuris yra lygus nuliui. Taigi gauname šias koordinačių ašies taškų koordinates:

4 apibrėžimas. Taško A abscisė yra taško koordinatėy(0;2);

By(0;1);

Cy(0;-2).

3 pavyzdys. Dekarto koordinačių sistemoje taškai pateikiami plokštumoje

4 apibrėžimas. Taško A abscisė yra taško koordinatė(2; 3) ;

B(-3; 2) ;

C(-1; -1) .

Jautis .

Jautis Jautis Jautis, turės tą pačią abscisę kaip ir nurodytas taškas, o ordinatė lygi absoliučioji vertė duoto taško ordinatė ir jos priešingas ženklas. Taigi gauname šias taškų koordinates, simetriškas šiems taškams ašies atžvilgiu Jautis :

A"(2; -3) ;

B"(-3; -2) ;

C"(-1; 1) .

Pats spręskite uždavinius naudodami Dekarto koordinačių sistemą, o tada peržiūrėkite sprendimus

4 pavyzdys. Nustatykite, kuriuose kvadrantuose (ketvirčiai, brėžinys su kvadrantais - pastraipos „Stačiakampė Dekarto koordinačių sistema plokštumoje“ pabaigoje) gali būti taškas M(x; arba) , Jei

1) xy > 0 ;

2) xy < 0 ;

3) x − arba = 0 ;

4) x + arba = 0 ;

5) x + arba > 0 ;

6) x + arba < 0 ;

7) x − arba > 0 ;

8) x − arba < 0 .

5 pavyzdys. Dekarto koordinačių sistemoje taškai pateikiami plokštumoje

4 apibrėžimas. Taško A abscisė yra taško koordinatė(-2; 5) ;

B(3; -5) ;

C(a; b) .

Raskite taškų, simetriškų šiems taškams, koordinates ašies atžvilgiu Oy .

Ir toliau spręskime problemas kartu

6 pavyzdys. Dekarto koordinačių sistemoje taškai pateikiami plokštumoje

4 apibrėžimas. Taško A abscisė yra taško koordinatė(-1; 2) ;

B(3; -1) ;

C(-2; -2) .

Raskite taškų, simetriškų šiems taškams, koordinates ašies atžvilgiu Oy .

Sprendimas. Pasukite 180 laipsnių aplink ašį Oy kryptinis segmentas nuo ašies Oy iki šios vietos. Paveikslėlyje, kur nurodyti plokštumos kvadrantai, matome, kad taškas yra simetriškas duotajam ašies atžvilgiu Oy, turės tą pačią ordinatę, kaip ir duotasis taškas, o abscisė absoliučia reikšme lygi nurodyto taško abscisei ir priešinga pagal ženklą. Taigi gauname šias taškų koordinates, simetriškas šiems taškams ašies atžvilgiu Oy :

A"(1; 2) ;

B"(-3; -1) ;

C"(2; -2) .

7 pavyzdys. Dekarto koordinačių sistemoje taškai pateikiami plokštumoje

4 apibrėžimas. Taško A abscisė yra taško koordinatė(3; 3) ;

B(2; -4) ;

C(-2; 1) .

Raskite taškų koordinates, simetriškas šiems taškams, atsižvelgiant į pradinę padėtį.

Sprendimas. Nukreiptą segmentą, einantį nuo pradžios iki nurodyto taško, pasukame 180 laipsnių aplink pradinę vietą. Paveikslėlyje, kur nurodyti plokštumos kvadrantai, matome, kad taškas, simetriškas nurodytam taškui koordinačių pradžios atžvilgiu, turės abscisę ir ordinatę pagal absoliučią vertę duotojo taško abscisei ir ordinatėms, tačiau priešingas ženklu. Taigi gauname šias taškų koordinates, simetriškas šiems taškams, atsižvelgiant į pradinę padėtį:

A"(-3; -3) ;

B"(-2; 4) ;

C(2; -1) .

8 pavyzdys.

4 apibrėžimas. Taško A abscisė yra taško koordinatė(4; 3; 5) ;

B(-3; 2; 1) ;

C(2; -3; 0) .

Raskite šių taškų projekcijų koordinates:

1) lėktuve Oxy ;

2) lėktuve Oxz ;

3) į lėktuvą Oyz ;

4) ant abscisių ašies;

5) ordinačių ašyje;

6) ant taikymo ašies.

1) Taško projekcija į plokštumą Oxy yra pačioje šioje plokštumoje, todėl turi abscisę ir ordinatę, lygią tam tikro taško abscisei ir ordinatėms, o aplikaciją lygi nuliui. Taigi gauname šias šių taškų projekcijų koordinates Oxy :

4 apibrėžimas. Taško A abscisė yra taško koordinatėxy (4; 3; 0);

Bxy (-3; 2; 0);

Cxy(2;-3;0).

2) Taško projekcija į plokštumą Oxz yra pačioje šioje plokštumoje, todėl turi abscisę ir aplikaciją, lygią tam tikro taško abscisei ir aplikacijai, o ordinatę lygi nuliui. Taigi gauname šias šių taškų projekcijų koordinates Oxz :

4 apibrėžimas. Taško A abscisė yra taško koordinatėxz (4; 0; 5);

Bxz (-3; 0; 1);

Cxz (2; 0; 0).

3) Taško projekcija į plokštumą Oyz yra pačioje šioje plokštumoje, todėl turi ordinatę ir taikymą, lygią tam tikro taško ordinatėms ir taikymui, o abscisę lygi nuliui. Taigi gauname šias šių taškų projekcijų koordinates Oyz :

4 apibrėžimas. Taško A abscisė yra taško koordinatėyz(0; 3; 5);

Byz (0; 2; 1);

Cyz (0; -3; 0).

4) Kaip matyti iš šios pamokos teorinės dalies, taško projekcija į abscisių ašį yra pačioje abscisių ašyje, ty ašyje Jautis, todėl turi abscisę, lygią paties taško abscisei, o projekcijos ordinatė ir aplikacija yra lygios nuliui (kadangi ordinatės ir aplikacinės ašys kerta abscises taške 0). Gauname šias šių taškų projekcijų į abscisių ašį koordinates:

4 apibrėžimas. Taško A abscisė yra taško koordinatėx (4; 0; 0);

Bx (-3; 0; 0);

Cx(2;0;0).

5) taško projekcija į ordinačių ašį yra pačioje ordinačių ašyje, ty ašyje Oy, todėl turi ordinatę, lygią paties taško ordinatėms, o projekcijos abscisė ir aplikacija yra lygios nuliui (nes abscisės ir aplikacinės ašys kerta ordinačių ašį taške 0). Gauname šias šių taškų projekcijų koordinates į ordinačių ašį:

4 apibrėžimas. Taško A abscisė yra taško koordinatėy(0; 3; 0);

By (0; 2; 0);

Cy(0;-3;0).

6) taško projekcija į taikymo ašį yra pačioje taikymo ašyje, ty ašyje Ozas, todėl turi aplikaciją, lygią paties taško aplikacijai, o projekcijos abscisė ir ordinatė lygios nuliui (kadangi abscisių ir ordinačių ašys kerta aplikacijos ašį taške 0). Gauname šias šių taškų projekcijų į taikomąją ašį koordinates:

4 apibrėžimas. Taško A abscisė yra taško koordinatėz (0; 0; 5);

Bz (0; 0; 1);

Cz(0; 0; 0).

9 pavyzdys. Dekarto koordinačių sistemoje taškai pateikiami erdvėje

4 apibrėžimas. Taško A abscisė yra taško koordinatė(2; 3; 1) ;

B(5; -3; 2) ;

C(-3; 2; -1) .

Raskite taškų koordinates, simetriškas šiems taškams, atsižvelgiant į:

1) lėktuvas Oxy ;

2) lėktuvai Oxz ;

3) lėktuvai Oyz ;

4) abscisių ašys;

5) ordinačių ašys;

6) pritaikyti ašis;

7) koordinačių kilmė.

1) „Perkelkite“ tašką kitoje ašies pusėje Oxy Oxy, turės abscisę ir ordinatę, lygią tam tikro taško abscisei ir ordinatėms, o aplikaciją, kurios dydis yra lygus duoto taško aplikacijai, bet priešingą ženklu. Taigi gauname tokias taškų koordinates, simetriškas duomenims plokštumos atžvilgiu Oxy :

A"(2; 3; -1) ;

B"(5; -3; -2) ;

C"(-3; 2; 1) .

2) „Perkelkite“ tašką kitoje ašies pusėje Oxzį tą patį atstumą. Iš paveikslo, kuriame pavaizduota koordinačių erdvė, matome, kad taškas yra simetriškas nurodytam taškui ašies atžvilgiu Oxz, turės abscisę ir aplikaciją, lygią duoto taško abscisei ir aplikacijai, o ordinatę, kurios dydis yra lygus tam tikro taško ordinatėms, bet priešingą ženklu. Taigi gauname tokias taškų koordinates, simetriškas duomenims plokštumos atžvilgiu Oxz :

A"(2; -3; 1) ;

B"(5; 3; 2) ;

C"(-3; -2; -1) .

3) „Perkelti“ tašką kitoje ašies pusėje Oyzį tą patį atstumą. Iš paveikslo, kuriame pavaizduota koordinačių erdvė, matome, kad taškas yra simetriškas nurodytam taškui ašies atžvilgiu Oyz, turės ordinatę ir aplicatę, lygias duoto taško ordinatėms ir aplicatams, o abscisę savo reikšme lygi duoto taško abscisei, bet priešingą ženklu. Taigi gauname tokias taškų koordinates, simetriškas duomenims plokštumos atžvilgiu Oyz :

A"(-2; 3; 1) ;

B"(-5; -3; 2) ;

C"(3; 2; -1) .

Pagal analogiją su simetriški taškai plokštumoje ir erdvės taškuose, simetriškuose duomenims plokštumų atžvilgiu, pažymime, kad esant simetrijai tam tikros Dekarto koordinačių sistemos erdvėje ašies atžvilgiu, koordinatė ašyje, kurios atžvilgiu yra nurodyta simetrija, bus išsaugo savo ženklą, o kitų dviejų ašių koordinatės absoliučiais skaičiais bus tokios pačios kaip tam tikro taško koordinatės, bet priešingos pagal ženklą.

4) Abscisė išsaugos savo ženklą, tačiau ordinatė ir aplikacija pakeis ženklus. Taigi gauname šias taškų koordinates, simetriškas duomenims abscisių ašies atžvilgiu:

A"(2; -3; -1) ;

B"(5; 3; -2) ;

C"(-3; -2; 1) .

5) Ordinata išsaugos savo ženklą, bet abscisė ir aplikacija pakeis ženklus. Taigi gauname tokias taškų koordinates, simetriškas duomenims, palyginti su ordinačių ašimi:

A"(-2; 3; -1) ;

B"(-5; -3; -2) ;

C"(3; 2; 1) .

6) Aplikacija išsaugos savo ženklą, tačiau abscisė ir ordinatė pakeis ženklus. Taigi gauname šias taškų koordinates, simetriškas duomenims taikomosios ašies atžvilgiu:

A"(-2; -3; 1) ;

B"(-5; 3; 2) ;

C"(3; -2; -1) .

7) Analogiškai su simetrija, kai taškai yra plokštumoje, kai yra simetrija apie koordinačių pradžią, visos taško koordinatės, simetriškos tam tikram taškui, absoliučia verte bus lygios tam tikro taško koordinatėms, bet priešingai jiems ženkle. Taigi gauname tokias taškų koordinates, simetriškas duomenims, palyginti su kilme.

Polinės koordinatės

Skambina numeriu poliarinis spindulys taškais arba pirmoji polinė koordinatė. Atstumas negali būti neigiamas, todėl bet kurio taško poliarinis spindulys yra . Taip pat pažymėta pirmoji polinė koordinatė Graikiškas laiškas(„ro“), bet aš pripratau prie lotyniškos versijos ir naudosiu ją ateityje.

Skambina numeriu poliarinis kampas duotas taškas arba antroji polinė koordinatė. Poliarinis kampas paprastai skiriasi viduje (vadinamasis pagrindinių kampų vertės). Tačiau gana priimtina naudoti diapazoną, o kai kuriais atvejais tiesioginis poreikis atsižvelgti į visas kampo reikšmes nuo nulio iki „pliuso begalybės“. Beje, rekomenduoju priprasti prie radianinio kampo mato, nes dirbate su laipsniais in aukštoji matematika laikomas ne comme il faut.

Pora vadinama poliarines koordinates taškais Juos lengva rasti ir konkrečias vertybes. Tangentas aštrus kampas stačiakampis - yra priešingos pusės ir gretimos pusės santykis: taigi pats kampas: . Pagal Pitagoro teoremą hipotenuzės kvadratas lygi sumai kojų kvadratai: taigi, poliarinis spindulys:

Taigi, .

Vienas pingvinas yra geras, bet kaimenė geriau:


Neigiamai orientuoti kampai Pažymėjau jį rodyklėmis tam atvejui, jei kas nors iš skaitytojų dar nežinotų apie šią orientaciją. Jei norite, prie kiekvieno iš jų galite „prisukti“ 1 posūkį (rad. arba 360 laipsnių) ir, beje, bus patogu. lentelės reikšmės:

Tačiau šių „tradiciškai“ orientuotų kampų trūkumas yra tas, kad jie „susukti“ per toli (daugiau nei 180 laipsnių) prieš laikrodžio rodyklę. Numatau klausimą: „kodėl trūksta ir kodėl jų trūksta neigiami kampai? Matematikoje trumpiausias ir racionaliais būdais. Na, o fizikos požiūriu sukimosi kryptis dažnai turi esminę reikšmę - kiekvienas iš mūsų bandėme atidaryti duris, patraukdami rankeną ne ta kryptimi =)

Taškų konstravimo poliarinėse koordinatėse tvarka ir technika

Gražios nuotraukos gražus, bet įmontuotas poliarinė sistema koordinates yra gana kruopštus uždavinys. Nėra jokių sunkumų su taškais, kurių poliariniai kampai yra , mūsų pavyzdyje tai yra taškai ; Vertės, kurios yra 45 laipsnių kartotiniai, taip pat nesukelia didelių problemų: . Bet kaip teisingai ir kompetentingai sukonstruoti, tarkime, tašką?

Jums reikės languoto popieriaus lapo, pieštuko ir šių dalykų piešimo įrankiai: liniuotė, kompasas, transporteris. IN kaip paskutinė priemonė, galite išsiversti tik su viena liniuote arba net... visai be jos! Skaitykite toliau ir gausite dar vieną įrodymą, kad ši šalis yra nenugalima =)

1 pavyzdys

Sukurkite tašką polinėje koordinačių sistemoje.

Visų pirma, reikia išsiaiškinti laipsnio matas kampu Jei kampas nepažįstamas arba kyla abejonių, visada geriau jį naudoti stalo arba bendroji radianų konvertavimo į laipsnius formulė. Taigi mūsų kampas yra (arba).

Nubraižykime polinę koordinačių sistemą (žr. pamokos pradžią) ir paimkime transporterį. Apvalaus instrumento savininkams nebus sunku pažymėti 240 laipsnių kampu, bet su didelė tikimybė Savo rankose turėsite pusapvalę įrenginio versiją. Problema visiškas nebuvimas transporteris, jei turite spausdintuvą ir žirkles išspręsta rankdarbiais.

Yra du būdai: apversti lapą ir pažymėti 120 laipsnių kampu arba „sukti“ pusę apsisukimo ir apžiūrėti priešingas kampas. Pasirinkime suaugusiųjų metodą ir pažymime 60 laipsnių:


Arba liliputinis matuoklis, arba milžiniškas narvas =) Tačiau norint išmatuoti kampą, skalė nėra svarbi.

Pieštuku nubrėžkite ploną tiesią liniją, einančią per stulpą ir padarytą ženklą:


Mes sutvarkėme kampą, dabar yra poliarinis spindulys. Paimk kompasą ir palei liniją mes nustatome jo sprendimą iki 3 vienetų, dažniausiai tai, žinoma, yra centimetrai:

Dabar atsargiai uždėkite adatą ant stulpo ir sukamasis judėjimas Padarome nedidelį serifą (raudonos spalvos). Reikalingas taškas buvo pastatytas:


Galite apsieiti be kompaso, uždėję liniuotę tiesiai ant sukonstruotos tiesės ir išmatuodami 3 centimetrus. Bet, kaip matysime vėliau, problemos, susijusios su konstravimu polinėje koordinačių sistemoje tipiška situacija, kai reikia pažymėti du arba didelis kiekis taškai su tuo pačiu poliariniu spinduliu, todėl efektyviau grūdinti metalą. Visų pirma, mūsų brėžinyje, pasukus kompaso koją 180 laipsnių kampu, lengva padaryti antrą įpjovą ir sukonstruoti tašką, simetrišką stulpo atžvilgiu. Panaudokime jį, kad peržiūrėtume medžiagą kitoje pastraipoje:

Stačiakampių ir polinių koordinačių sistemų ryšys

Aišku pridėkimeį poliarinę koordinačių sistemą, „įprastą“ koordinačių tinklelį ir nubrėžkite tašką brėžinyje:

Visada naudinga nepamiršti šio ryšio braižant polines koordinates. Nors, norom nenorom, jis užsimena be jokios papildomos užuominos.

Nustatykime ryšį tarp polinių ir Dekarto koordinačių naudodami pavyzdį konkretus taškas. Pasvarstykime taisyklingas trikampis, kurioje hipotenuzė lygi poliariniam spinduliui: , o kojos lygios taško „X“ ir „Y“ koordinatėms Dekarto koordinačių sistemoje: .

Smagiojo kampo sinusas yra priešingos pusės ir hipotenuzės santykis:

Smailiojo kampo kosinusas yra santykis gretima kojaį hipotenuzę:

Kartu pakartojome sinuso, kosinuso (ir kiek ankstesnio liestinės) apibrėžimus iš bendrojo lavinimo mokyklos 9 klasės programos.

Į savo žinyną įtraukite darbines formules, kurios išreiškia taško Dekarto koordinates per jo polines koordinates – su jomis teks susidoroti ne kartą, o kitą kartą jau dabar =)

Raskime taško koordinates stačiakampė sistema koordinatės:

Taigi:

Gautos formulės atveria dar vieną spragą konstravimo uždavinyje, kai galima apsieiti ir be transporterio: pirmiausia surandame taško Dekarto koordinates (žinoma, juodraštyje), tada mintyse randame tinkamą vietą brėžinyje. ir pažymėkite šį tašką. Įjungta paskutinis etapas nubrėžkite ploną tiesią liniją, kuri eina per pastatytą tašką ir ašigalį. Dėl to paaiškėja, kad kampas tariamai buvo matuojamas transporteriu.

Smagu, kad labai beviltiški mokiniai gali išsiversti net be liniuotės, o vietoj jos naudoja lygią vadovėlio, sąsiuvinio ar pažymių knyga– juk nešiojamųjų kompiuterių gamintojai pasirūpino metrikais, 1 celė = 5 milimetrai.

Visa tai man priminė gerai žinomą pokštą, kuriame išradingi pilotai suplanavo kursą kartu su Belomor paketu =) Nors, juokais atmetus, pokštas nėra taip toli nuo realybės, prisimenu, kad viename iš vidaus skrydžių rusiškai. Federacija, sugedo visi lėktuvo navigacijos prietaisai, o įgula sėkmingai nusileidau į lėktuvą naudojant įprastą vandens stiklinę, kuri rodė lėktuvo kampą žemės atžvilgiu. O pakilimo takas – štai, matosi iš priekinio stiklo.

Naudojant pamokos pradžioje cituotą Pitagoro teoremą, tai lengva gauti atvirkštinės formulės: , taigi:

Pats kampas „phi“ paprastai išreiškiamas per arctangentą - visiškai toks pat kaip kompleksinio skaičiaus argumentas su visomis savo bėdomis.

Taip pat patartina į savo orientacinį bagažą sutalpinti antrąją mišinių grupę.

Po to išsamią analizę skrydžiai su atskirais taškais, pereikime prie natūralios temos tęsinio:

Tiesės lygtis polinėmis koordinatėmis

Iš esmės tiesės lygtis polinėje koordinačių sistemoje yra poliarinio spindulio nuo poliarinio kampo funkcija (argumentas). Šiuo atveju atsižvelgiama į polinį kampą radianais(!) Ir nuolat paima reikšmes nuo iki (kartais tai turėtų būti laikoma iki begalybės arba dėl patogumo daugelyje problemų nuo iki). Kiekviena įtraukta kampo „phi“ reikšmė domenas funkcija, atitinka vieną poliarinio spindulio reikšmę.

Poliarinę funkciją galima palyginti su savotišku radaru – kai iš stulpo sklindantis šviesos spindulys sukasi prieš laikrodžio rodyklę ir „aptinka“ (nubrėžia) liniją.

Standartinis poliarinės kreivės pavyzdys yra Archimedo spiralė. Toliau pateiktame paveikslėlyje ji pavaizduota Pirmas raundas– kai polinis spindulys po poliarinio kampo įgyja reikšmes nuo 0 iki:

Be to, taške kirsdama poliarinę ašį, spiralė toliau vyniosis, judėdama be galo toli nuo ašigalio. Bet panašių atvejų praktiškai jie yra gana reti; daugiau tipiška situacija, kai visuose vėlesniuose apsisukimuose mes „einame ta pačia linija“, kuri buvo gauta diapazone.

Pirmajame pavyzdyje mes susiduriame su koncepcija apibrėžimo sritis polinė funkcija: kadangi poliarinis spindulys yra neneigiamas, čia negalima atsižvelgti į neigiamus kampus.

! Pastaba : kai kuriais atvejais įprasta naudoti apibendrintos polinės koordinatės, kur spindulys gali būti neigiamas, ir šį metodą trumpai išnagrinėsime šiek tiek vėliau

Be Archimedo spiralės, yra daug kitų žinomų kreivių, tačiau, kaip sakoma, meno neužtenka, todėl atrinkau pavyzdžius, kurie labai dažnai sutinkami realiose praktinėse užduotyse.

Pirma, paprasčiausios lygtys ir paprasčiausios linijos:

Formos lygtis nurodo tą, kuri kyla iš poliaus Rėjus. Iš tiesų, pagalvokite apie tai, jei kampo vertė Visada(kad ir koks būtų „er“) nuolat, tai kokia tai linija?

Pastaba : apibendrintoje polinių koordinačių sistemoje duota lygtis apibrėžia tiesę, einanti per ašigalį

Formos lygtis lemia... pirmą kartą atspėkite – jei bet kam Kampo "phi" spindulys išlieka pastovus? Tiesą sakant, tai yra apibrėžimas ratas centruotas spindulio poliuje .

Pavyzdžiui, . Aiškumo dėlei suraskime šios tiesės lygtį stačiakampėje koordinačių sistemoje. Naudodami formulę, gautą ankstesnėje pastraipoje, pakeičiame:

Palyginkime abi puses:

– apskritimo lygtis su centru 2 spindulio pradžioje, o tai ir reikėjo patikrinti.

Nuo straipsnio sukūrimo ir išleidimo apie vektorių tiesinę priklausomybę ir tiesinę nepriklausomybę Gavau keletą laiškų iš svetainės lankytojų, kurie uždavė klausimą tokia dvasia: „yra paprasta ir patogi stačiakampė koordinačių sistema, kam mums reikia kitos įstrižinės? afininis atvejis?. Atsakymas paprastas: matematika siekia aprėpti viską ir visus! Be to, tam tikroje situacijoje patogumas yra svarbus – kaip matote, daug pelningiau dirbti su apskritimu poliarinėse koordinatėse dėl itin didelio lygties paprastumo.

Ir kartais matematinis modelis numato mokslo atradimai. Taigi vienu metu Kazanės universiteto rektorius N.I. Lobačevskis griežtai įrodyta, per savavališkas taškas galima piešti plokštumas be galo daug tiesių linijų, lygiagrečiai šiam. Dėl to jį viskas apšmeižė mokslo pasaulis, bet... paneigti Šis faktas niekas negalėjo. Tik po gero šimtmečio astronomai atrado, kad šviesa erdvėje sklinda išlenktomis trajektorijomis, kur pradeda veikti Lobačevskio neeuklidinė geometrija, formaliai jo sukurta gerokai prieš šį atradimą. Daroma prielaida, kad tai yra pačios erdvės savybė, kurios kreivumas mums nematomas dėl mažų (astronominiais standartais) atstumų.

Panagrinėkime prasmingesnes statybos užduotis:

2 pavyzdys

Sukurkite liniją

Sprendimas: pirmiausia suraskime domenas. Kadangi poliarinis spindulys yra neneigiamas, nelygybė turi galioti. Galite prisiminti mokyklos taisykles, kaip spręsti trigonometrines nelygybes, bet paprasti atvejai kaip šis, rekomenduoju greičiau ir vizualinis metodas sprendimai:

Įsivaizduokite kosinuso grafiką. Jei jis dar neužregistruotas jūsų atmintyje, suraskite jį puslapyje Elementariųjų funkcijų grafikai. Ką mums sako nelygybė? Tai mums sako, kad kosinuso grafikas turi būti išdėstytas ne mažiau abscisių ašis. Ir tai atsitinka segmente. Ir, atitinkamai, intervalas netinka.

Taigi, mūsų funkcijos apibrėžimo sritis yra: , tai yra, grafikas yra dešinėje ašigalio pusėje (Dekarto sistemos terminologijoje - dešinėje pusplokštumoje).

Poliarinėse koordinatėse dažnai yra miglota idėja, kuri tiesė apibrėžia konkrečią lygtį, todėl norint ją sudaryti, reikia rasti jai priklausančius taškus – ir kuo daugiau, tuo geriau. Paprastai jie apsiriboja keliolika ar dviem (ar net mažiau). Paprasčiausias būdas, žinoma, yra imtis lentelės kampų vertės. Siekiant didesnio aiškumo, neigiamos reikšmės„Prisuksiu“ vieną posūkį:

Dėl kosinuso pariteto Aktualus teigiamas vertes nereikia dar kartą skaičiuoti:

Pavaizduokime polinę koordinačių sistemą ir nubraižykime rastus taškus, while tos pačios vertybės Patogu vienu metu atidėti „er“, naudojant kompasą, naudojant aukščiau aptartą technologiją:

Iš esmės linija yra aiškiai nubrėžta, tačiau norėdami visiškai patvirtinti spėjimą, suraskime jos lygtį Dekarto koordinačių sistemoje. Galite taikyti neseniai gautas formules , bet papasakosiu apie gudresnį triuką. Dirbtinai padauginame abi lygties puses iš „er“: ir naudojame kompaktiškesnes perėjimo formules:

Paryškinimas tobulas kvadratas, mes pateikiame linijos lygtį į atpažįstamą formą:

– apskritimo lygtis su centru taške , spindulys 2.

Kadangi pagal būklę tiesiog reikėjo atlikti statybą ir viskas, rastus taškus sklandžiai sujungiame linija:

Paruošta. Gerai, jei jis pasirodys šiek tiek nelygus, jūs neturėjote žinoti, kad tai buvo ratas ;-)

Kodėl neatsižvelgėme į kampo vertes už intervalo ribų? Atsakymas paprastas: nėra prasmės. Dėl funkcijos periodiškumo susiduriame su begaliniu bėgimu sukonstruotu apskritimu.

Nesunku atlikti paprastą analizę ir padaryti išvadą, kad formos lygtis nurodo skersmens apskritimą, kurio centras yra taške. Vaizdžiai tariant, visi tokie apskritimai „sėdi“ ant poliarinės ašies ir būtinai eina per ašigalį. Jei tada juokinga kompanija migruos į kairę – į poliarinės ašies tęsinį (pagalvokite kodėl).

Panaši užduotis savarankiškas sprendimas:

3 pavyzdys

Sukurkite tiesę ir raskite jos lygtį stačiakampėje koordinačių sistemoje.

Susisteminkime problemos sprendimo procedūrą:

Pirmiausia randame funkcijos apibrėžimo sritį, į kurią patogu pažvelgti sinusoidinė iš karto suprasti, kur sinusas yra neneigiamas.

Antrame žingsnyje apskaičiuojame taškų polines koordinates naudodami lentelės kampų vertės; Išanalizuoti, ar įmanoma sumažinti skaičiavimų skaičių?

Trečiame žingsnyje nubrėžiame taškus poliarinėje koordinačių sistemoje ir atsargiai sujungiame juos linija.

Ir galiausiai randame tiesės lygtį Dekarto koordinačių sistemoje.

Apytikslis pavyzdys sprendimai pamokos pabaigoje.

Bendras algoritmas o poliarinėmis koordinatėmis detalizuojame statybos techniką
ir žymiai pagreitinti antroje paskaitos dalyje, bet prieš tai susipažinsime su kita bendra linija:

Poliarinė rožė

Tai tiesa, mes kalbame apie gėlę su žiedlapiais:

4 pavyzdys

Sukonstruoti tieses, pateiktas lygtimis polinėmis koordinatėmis

Yra du poliarinės rožės kūrimo būdai. Pirmiausia sekime raižytą takelį, darydami prielaidą, kad poliarinis spindulys negali būti neigiamas:

Sprendimas:

a) Raskime funkcijos apibrėžimo sritį:

Tai trigonometrinė nelygybė Tai taip pat nesunku išspręsti grafiškai: iš straipsnio medžiagos Geometrinės grafikų transformacijosžinoma, kad jei funkcijos argumentas padvigubinamas, tai jos grafikas iki ordinačių ašies susitrauks 2 kartus. Pirmame pavyzdyje raskite funkcijos grafiką nurodytą pamoką. Kur yra šis sinusoidas virš x ašies? Protarpiais . Vadinasi, nelygybę tenkina atitinkami segmentai, ir domenas mūsų funkcija: .

Paprastai kalbant, nagrinėjamos nelygybės sprendimas yra sąjunga begalinis skaičius segmentus, bet, vėlgi, mus domina tik vienas laikotarpis.

Galbūt kai kuriems skaitytojams bus lengviau analitinis metodas radęs apibrėžimo sritį, sąlyginai tai pavadinsiu „apvalaus pyrago pjaustymu“. Supjaustysime į lygias dalis ir, visų pirma, suraskite pirmojo kūrinio ribas. Mes motyvuojame taip: sinusas yra neneigiamas, Kada jo argumentas svyruoja nuo 0 iki rad. imtinai. Mūsų pavyzdyje: . Padalinę visas dvigubos nelygybės dalis iš 2, gauname reikiamą intervalą:

Dabar pradedame nuosekliai „pjauti lygius 90 laipsnių gabalus“ prieš laikrodžio rodyklę:

– rastas segmentas, žinoma, įtraukiamas į apibrėžimo sritį;

– kitas intervalas – neįskaičiuotas;

– kitas segmentas – įtrauktas;

– ir galiausiai, intervalas – neįtrauktas.

Visai kaip ramunė - "myli, nemyli, myli, nemyli" =) Su tuo skirtumu, kad čia nėra ateities. Taip, tai tik kažkokia meilė kiniškai…

Taigi, o linija reiškia rožę su dviem vienodais žiedlapiais. Gana priimtina brėžinį braižyti schematiškai, tačiau labai patartina teisingai surasti ir pažymėti žiedlapių viršūnės. Viršūnės atitinka apibrėžimo srities atkarpų vidurio taškai, kuriame šiame pavyzdyje turi akivaizdžias kampines koordinates . Kuriame žiedlapių ilgiai yra:

Štai natūralus rūpestingo sodininko rezultatas:

Pažymėtina, kad žiedlapio ilgį galima nesunkiai matyti iš lygties – kadangi sinusas yra ribotas: , tada maksimali vertė„er“ tikrai neviršys dviejų.

b) Nustatykime liniją, pateikta lygtimi. Akivaizdu, kad šios rožės žiedlapio ilgis taip pat yra du, bet pirmiausia mus domina apibrėžimo sritis. Taikoma analitinis metodas"kirpimai": sinusas yra neneigiamas, kai jo argumentas yra diapazone nuo nulio iki „pi“ imtinai, in tokiu atveju: . Visas nelygybės dalis padaliname iš 3 ir gauname pirmąjį intervalą:

Toliau mes pradedame "pjaustyti pyragą į gabalus" pagal rad. (60 laipsnių):
– segmentas pateks į apibrėžimo sritį;
– intervalas – nebus įtrauktas;
– segmentas – tiks;
– intervalas – nebus įtrauktas;
– segmentas – tiks;
– intervalas – nebus įtrauktas.

Procesas sėkmingai baigtas 360 laipsnių kampu.

Taigi apibrėžimo apimtis yra tokia: .

Veiksmus, atliekamus visiškai arba iš dalies, lengva atlikti protiškai.

Statyba. Jei ankstesnėje pastraipoje viskas pavyko gerai su stačiu kampu ir 45 laipsnių kampu, tada čia turėsite šiek tiek pasitempti. Raskime žiedlapių viršūnės. Jų ilgis buvo matomas nuo pat užduoties pradžios, belieka apskaičiuoti kampines koordinates, kurios yra lygios apibrėžimo srities atkarpų vidurio taškams:

Atkreipkite dėmesį, kad tarp žiedlapių viršūnių turi būti vienodi tarpai, šiuo atveju 120 laipsnių.

Patartina brėžinį pažymėti į 60 laipsnių kampus (ribotus žalios linijos) ir nubrėžkite žiedlapių viršūnių kryptis (pilkos linijos). Patogu kompasu pažymėti pačias viršūnes – vieną kartą išmatuokite 2 vienetų atstumą ir nubrėžtomis 30, 150 ir 270 laipsnių kryptimis padarykite tris įpjovas:

Paruošta. Suprantu, kad tai varginanti užduotis, bet jei nori viską protingai sutvarkyti, teks skirti laiko.

Suformuluokime bendroji formulė : formos lygtis , – natūralusis skaičius), apibrėžia poliarinę rožę, kurios žiedlapio ilgis lygus .

Pavyzdžiui, lygtis nurodo keturlapį, kurio žiedlapio ilgis yra 5 vienetai, lygtis nurodo 5 žiedlapių rožę, kurios žiedlapio ilgis yra 3 vienetai. ir tt