Gerekli numara bulundu: a 0 = k − 1 (\displaystyle a_(0)=k-1).

İkinci kez Arşimet aksiyomu örtülü olarak dizi parçalarının uzunluklarının sıfıra eğilimli olduğunu kanıtlamak için kullanıldı. ben 0 , ben 1 , ben 2 , … (\displaystyle I_(0),I_(1),I_(2),\ldots ):

Bu önerinin kesin bir kanıtı Arşimed'in aksiyomuna dayanmaktadır. Eşdeğer ilişkiyi kanıtlayalım

Arşimet aksiyomuna göre gerçek sayı ne olursa olsun E > 0 (\displaystyle E>0), doğal sayılar dizisi 1 , 2 , … (\displaystyle 1,2,\ldots) belli bir sayıdan başlayarak onu aşacaktır. Ve herkes için olduğundan n (\displaystyle n) eşitsizlik var

sonra sıra 10 n (\displaystyle 10^(n)) da aşacak E (\displaystyle E), aynı numaradan başlayarak. Sayı dizisinin tanımına göre bu şu anlama gelir: lim n → ∞ 10 n = ∞ (\displaystyle \lim _(n\to \infty )10^(n)=\infty ).

Ondalık gösterim belirsizliği

Yukarıdaki algoritmayı kullanarak herhangi bir gerçek sayı için bunu yapabiliriz. α (\displaystyle \alpha ) Belirli bir sayıyı temsil eden bir ondalık kesir oluşturun. Ancak aynı sayıda da olabilir α (\displaystyle \alpha ) ondalık kesir olarak ve başka şekillerde temsil edilebilir.

Sayıları ondalık kesirler biçiminde temsil etmenin benzersiz olmaması, zaten son kesire ondalık noktadan sonra sağa sıfırlar atayarak, aynı sayıyı temsil eden resmi olarak farklı ondalık kesirler elde edeceğimiz önemsiz gerçeğinden kaynaklanmaktadır.

Örneğin ondalık kesri düşünün

Tanım gereği bu kesir bir sayının temsilidir 0 + 9/10 + 9/100 + … = 1 (\displaystyle 0+9/10+9/100+\ldots =1). Ancak bu sayı ondalık kesir olarak da gösterilebilir. 1 , 00 … (\displaystyle 1(,)00\ldots ).

Bu örnek genelleştirilebilir. Kesirlerin olduğu gösterilebilir

Nerede a n ≠ 9 (\displaystyle a_(n)\neq 9), aynı gerçek sayıyı temsil eder.

Bu genel örneğin, gerçek sayıların ondalık kesirler biçiminde temsilindeki tüm belirsizlik durumlarını kapsadığı ortaya çıktı. Bu durumda, elbette, birbirinin sonuna sıfır eklenerek elde edilen kesirlerin yanı sıra bir çift kesir ve ve ile elde edilen önemsiz kesir durumlarını dikkate almıyoruz.

Bu sonuçlar aşağıdaki teoremde özetlenebilir.

Teorem. Herhangi bir gerçek sayı α (\displaystyle \alpha ), formda temsil edilemez p / 10 s (\displaystyle p/10^(s)), Nerede p (\displaystyle p)- tüm, s (\displaystyle s)- Negatif olmayan bir tam sayı, ondalık kesir biçiminde tek bir gösterimi kabul eder; Üstelik bu kesir sonsuzdur.

Formun herhangi bir gerçek sayısı α = p / 10 s (\displaystyle \alpha =p/10^(s)) ondalık sayı olarak birden fazla şekilde gösterilebilir. Eğer α ≠ 0 (\displaystyle \alpha \neq 0), o zaman sonlu bir ondalık kesir olarak veya ondalık noktadan sonraki sonuna sıfır eklenerek elde edilen sonsuz bir kesir olarak veya ile biten sonsuz bir kesir olarak temsil edilebilir. Sayı α = 0 (\displaystyle \alpha =0) formun kesirleriyle temsil edilebilir + 0 , 00 … (\displaystyle +0(,)00\ldots) ve formun kesirleri − 0 , 00 … (\displaystyle -0(,)00\ldots).

Yorum. ile biten sonsuz kesirler 999 … (\displaystyle 999\ldots), yukarıdaki algoritmada her zaman seçersek elde edilir sol bölüm yerine Sağ.

Fazladan sıfırlar ve hata

Bakış açısına göre, sonunda sıfır olan bir ondalık kesir yazmanın, onu bu sıfırlar olmadan yazmakla tamamen aynı olmadığı unutulmamalıdır.

Hata belirtilmemişse, ondalık kesrin artı veya eksi yarısına eşit olduğu genel olarak kabul edilir. ] son ​​yazılan rakamın birimleri. Örneğin “3,7” yazmak mutlak hatanın ±0,05 olduğu anlamına gelir. Ve “3,700” girişindeki mutlak hata ±0,0005'tir. Diğer örnekler:

• “25” - mutlak hata ±0,5'tir (ayrıca böyle bir giriş, 25'in tam değeri anlamına da gelebilir: örneğin, 25 adet);
• “25,0” - mutlak hata ±0,05'tir;
• “25,00”—mutlak hata ±0,005'tir.

Periyodik ondalıklar

Sonsuz ondalık kesir denir periyodik virgülden sonraki rakam dizisi belirli bir yerden başlayarak periyodik olarak tekrarlanan bir rakam grubu ise. Başka bir deyişle, periyodik bir kesir, formun ondalık kesiridir.

Bu kesir genellikle şu şekilde kısaca yazılır:

Tekrarlanan sayı grubu b 1 … b l (\displaystyle b_(1)\ldots b_(l)) isminde dönem Kesirlerde bu gruptaki basamak sayısı periyodun uzunluğudur.

Periyodik kesirlerde periyot virgülden hemen sonra geliyorsa kesre denir. saf periyodik. Ondalık virgül ile ilk nokta arasında sayılar varsa kesre denir. karışık periyodik ve ilk nokta işaretinden önceki ondalık noktadan sonraki rakam grubu ön dönem kesirler Örneğin, kesir 1 , (23) = 1,232 3 … (\displaystyle 1(,)(23)=1(,)2323\ldots ) saf periyodiktir ve kesir 0 , 1 (23) = 0,123 23 … (\displaystyle 0(,)1(23)=0(,)12323\ldots )- karışık periyodik.

Periyodik kesirlerin tüm ondalık kesirler kümesinden ayırt edildikleri ana özelliği, periyodik kesirlerin yalnızca temsil edilmesidir. Daha doğrusu aşağıdaki önerme geçerlidir.

Teorem. Her sonsuz periyodik ondalık kesir bir rasyonel sayıyı temsil eder. Tersine, eğer bir rasyonel sayı sonsuz bir ondalık kesire genişletilirse, bu kesir periyodiktir.

Tamamen periyodik kesirlerin, indirgenemez kesir olarak yazılan rasyonel sayılara karşılık geldiği gösterilebilir. p / q (\displaystyle p/q) payda q (\displaystyle q) sahip değil

Bu yazıda keşfetmeye başlayacağız rasyonel sayılar. Burada rasyonel sayıların tanımlarını vereceğiz, gerekli açıklamaları yapıp rasyonel sayılara örnekler vereceğiz. Bundan sonra verilen bir sayının rasyonel olup olmadığının nasıl belirleneceğine odaklanacağız.

Sayfada gezinme.

Rasyonel sayıların tanımı ve örnekleri

Bu bölümde rasyonel sayıların çeşitli tanımlarını vereceğiz. İfadelerdeki farklılıklara rağmen, bu tanımların tümü aynı anlama sahiptir: tıpkı tam sayıların doğal sayıları, onların zıttlarını ve sıfır sayısını birleştirmesi gibi, rasyonel sayılar da tam sayıları ve kesirleri birleştirir. Başka bir deyişle rasyonel sayılar tam sayıları genelleştirir ve kesirli sayılar.

Şununla başlayalım: rasyonel sayıların tanımları, bu en doğal şekilde algılanır.

Belirtilen tanımdan rasyonel bir sayının şu olduğu anlaşılmaktadır:

• Herhangi doğal sayı N. Aslında herhangi bir doğal sayıyı sıradan bir kesir olarak temsil edebilirsiniz, örneğin 3=3/1.
• Herhangi bir tam sayı, özellikle sıfır sayısı. Aslında herhangi bir tam sayı pozitif kesir, negatif kesir veya sıfır olarak yazılabilir. Örneğin, 26=26/1, .
• Herhangi bir ortak kesir (pozitif veya negatif). Bu, rasyonel sayıların verilen tanımıyla doğrudan doğrulanır.
• Herhangi bir karışık sayı. Aslında, karışık bir sayıyı her zaman uygunsuz bir kesir olarak temsil edebilirsiniz. Örneğin ve.
• Herhangi bir sonlu ondalık kesir veya sonsuz periyodik kesir. Bunun nedeni, belirtilen ondalık kesirlerin sıradan kesirlere dönüştürülmesidir. Örneğin, ve 0,(3)=1/3.

Ayrıca herhangi bir sonsuz periyodik olmayan ondalık kesirin rasyonel bir sayı OLMADIĞI açıktır, çünkü ortak bir kesir olarak temsil edilemez.

Artık rahatlıkla verebiliriz rasyonel sayılara örnekler. 4, 903, 100,321 sayıları doğal sayılar olduğundan rasyonel sayılardır. 58, −72, 0, −833,333,333 tam sayıları da rasyonel sayılara örnektir. Ortak kesirler 4/9, 99/3 de rasyonel sayılara örnektir. Rasyonel sayılar da sayıdır.

Yukarıdaki örneklerden hem pozitif hem de negatif rasyonel sayıların olduğu ve sıfır rasyonel sayısının ne pozitif ne de negatif olduğu açıktır.

Rasyonel sayıların yukarıdaki tanımı daha kısa bir biçimde formüle edilebilir.

Tanım.

Rasyonel sayılar z/n kesri olarak yazılabilen sayılardır; burada z bir tamsayı ve n bir doğal sayıdır.

Rasyonel sayıların bu tanımının önceki tanıma eşdeğer olduğunu kanıtlayalım. Bir kesir çizgisini bir bölme işareti olarak düşünebileceğimizi biliyoruz, o zaman tam sayıları bölmenin özelliklerinden ve tam sayıları bölme kurallarından aşağıdaki eşitliklerin geçerliliği takip edilir ve. İşte bunun kanıtı.

Rasyonel sayılara örnekler verelim bu tanım. −5, 0, 3 ve sayıları rasyonel sayılardır, çünkü bunlar sırasıyla bir tamsayı payı ve doğal paydası ile kesirler olarak yazılabilinir.

Rasyonel sayıların tanımı aşağıdaki formülle verilebilir.

Tanım.

Rasyonel sayılar sonlu veya sonsuz periyodik ondalık kesir olarak yazılabilen sayılardır.

Bu tanım aynı zamanda ilk tanıma da eşdeğerdir, çünkü her sıradan kesir sonlu veya periyodik bir ondalık kesire karşılık gelir ve bunun tersi de geçerlidir ve herhangi bir tam sayı, ondalık noktadan sonra sıfır bulunan bir ondalık kesirle ilişkilendirilebilir.

Örneğin 5, 0, −13 sayıları rasyonel sayılara örnektir çünkü aşağıdaki ondalık kesirler olarak yazılabilirler: 5,0, 0,0, −13,0, 0,8 ve −7, (18).

Bu noktanın teorisini aşağıdaki ifadelerle bitirelim:

• tamsayılar ve kesirler (pozitif ve negatif) rasyonel sayılar kümesini oluşturur;
• her rasyonel sayı, bir tamsayı payı ve bir doğal paydası olan bir kesir olarak temsil edilebilir ve bu tür kesirlerin her biri, belirli bir rasyonel sayıyı temsil eder;
• her rasyonel sayı, sonlu veya sonsuz periyodik ondalık kesir olarak temsil edilebilir ve bu tür kesirlerin her biri, bir rasyonel sayıyı temsil eder.

Bu sayı rasyonel midir?

Önceki paragrafta, herhangi bir doğal sayının, herhangi bir tam sayının, herhangi bir sıradan kesirin, herhangi bir karışık sayının, herhangi bir sonlu ondalık kesirin yanı sıra herhangi bir periyodik ondalık kesirin rasyonel bir sayı olduğunu öğrendik. Bu bilgi, bir dizi yazılı sayıdan rasyonel sayıları “tanımamızı” sağlar.

Peki ya sayı bazı şeklinde verilirse, ya da nasıl vb. sorusuna nasıl cevap verilir? verilen numara akılcı? Çoğu durumda cevap vermek çok zordur. Bazı düşünce yönlerini belirtelim.

Numara formda verilmişse sayısal ifade yalnızca rasyonel sayılar ve işaretler içeren aritmetik işlemler(+, −, · ve:) ise bu ifadenin değeri rasyonel bir sayıdır. Bu, rasyonel sayılarla yapılan işlemlerin nasıl tanımlandığından kaynaklanmaktadır. Örneğin ifadedeki tüm işlemleri yaptıktan sonra 18 rasyonel sayısını elde ederiz.

Bazen ifadeleri basitleştirdikten ve daha fazlasını yaptıktan sonra karmaşık tip belirli bir sayının rasyonel olup olmadığını belirlemek mümkün hale gelir.

Devam edelim. Her doğal sayı rasyonel olduğundan 2 sayısı rasyonel bir sayıdır. Peki ya sayı? Mantıklı mı? Hayır, bunun rasyonel bir sayı olmadığı, irrasyonel bir sayı olduğu ortaya çıktı (bu gerçeğin çelişkili kanıtı, aşağıda referans listesinde listelenen 8. sınıf cebir ders kitabında verilmiştir). Ayrıca kanıtlanmıştır ki karekök Bir doğal sayının rasyonel sayısı, yalnızca kökün bir doğal sayının tam karesi olan bir sayı içerdiği durumlarda rasyonel bir sayıdır. Örneğin, ve sayıları rasyonel sayılardır, çünkü 81 = 9 2 ve 1 024 = 32 2 ve ve sayıları rasyonel değildir, çünkü 7 ve 199 sayıları rasyonel değildir. mükemmel kareler doğal sayılar.

Sayı rasyonel mi değil mi? İÇİNDE bu durumda Dolayısıyla bu sayının rasyonel olduğunu görmek kolaydır. Sayı rasyonel mi? Bir tam sayının k'inci kökünün, yalnızca kök işaretinin altındaki sayının bir tamsayının k'inci kuvveti olması durumunda rasyonel sayı olduğu kanıtlanmıştır. Dolayısıyla beşinci kuvveti 121 olan bir tam sayı bulunmadığından rasyonel bir sayı değildir.

Çelişki yöntemi, bazı sayıların logaritmasının bazı nedenlerden dolayı rasyonel sayılar olmadığının kanıtlanmasına olanak tanır. Örneğin - sayısının rasyonel bir sayı olmadığını kanıtlayalım.

Bunun tersini varsayalım, yani bunun rasyonel bir sayı olduğunu ve m/n sıradan kesri olarak yazılabildiğini varsayalım. Daha sonra aşağıdaki eşitlikleri veriyoruz: . Son eşitlik imkansızdır çünkü sol tarafta tek sayı 5 n ve sağ tarafta çift sayı 2 m var. Dolayısıyla varsayımımız yanlıştır, dolayısıyla rasyonel bir sayı değildir.

Sonuç olarak, sayıların rasyonelliğini veya irrasyonelliğini belirlerken ani sonuçlara varmaktan kaçınılması gerektiğini özellikle belirtmekte fayda var.

Örneğin, irrasyonel sayılar π ve e'nin çarpımının irrasyonel bir sayı olduğunu hemen iddia etmemelisiniz; bu "görünüşte açık" ama kanıtlanmadı. Bu şu soruyu gündeme getiriyor: "Bir ürün neden rasyonel sayı olsun?" Neden olmasın, çünkü çarpımı rasyonel bir sayı veren irrasyonel sayılara bir örnek verebilirsiniz: .

Sayıların ve daha birçok sayının rasyonel olup olmadığı da bilinmiyor. Örneğin, var irrasyonel sayılar, irrasyonel derece bu bir rasyonel sayıdır. Örnek olarak, formun bir derecesini sunuyoruz, bu derecenin tabanı ve üssü rasyonel sayılar değil, ve 3 rasyonel bir sayıdır.

Referanslar.

• Matematik. 6. sınıf: eğitici. genel eğitim için kurumlar / [N. Ya. Vilenkin ve diğerleri]. - 22. baskı, rev. - M.: Mnemosyne, 2008. - 288 s.: hasta. ISBN 978-5-346-00897-2.
• Cebir: ders kitabı 8. sınıf için. genel eğitim kurumlar / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; tarafından düzenlendi S. A. Telyakovsky. - 16. baskı. - M.: Eğitim, 2008. - 271 s. : hasta. - ISBN 978-5-09-019243-9.
• Gusev V.A., Mordkovich A.G. Matematik (teknik okullara girenler için bir el kitabı): Proc. ödenek.- M.; Daha yüksek okul, 1984.-351 s., hasta.

İÇİNDE bu ders Rasyonel sayıların çarpımı ve bölünmesi dikkate alınır.

Rasyonel Sayılarla Çarpma

Tam sayılarda çarpma kuralları rasyonel sayılar için de geçerlidir. Başka bir deyişle rasyonel sayıları çarpmak için şunları yapabilmeniz gerekir:

Ayrıca, çarpmanın değişmeli kanunu, birleşmeli çarpma kanunu, çarpma ve sıfırla çarpmanın dağılım kanunu gibi temel çarpma yasalarını da bilmeniz gerekir.

Örnek 1. Bir ifadenin değerini bulun

Bu rasyonel sayıların çarpımıdır. farklı işaretler. Rasyonel sayıları farklı işaretlerle çarpmak için modüllerini çarpmanız ve ortaya çıkan cevabın önüne bir eksi koymanız gerekir.

Farklı işaretlere sahip sayılarla uğraştığımızı açıkça görmek için, her rasyonel sayıyı işaretleriyle birlikte parantez içine alıyoruz.

Sayının modülü eşittir ve sayının modülü eşittir. Ortaya çıkan modülleri şu şekilde çarpıyoruz: pozitif kesirler, bir cevap aldık ama kural gereği cevabın önüne bir eksi koyduk. Cevaptan önce bu eksiyi sağlamak için modüllerin çarpımı parantez içinde yapıldı ve önünde bir eksi vardı.

Kısa çözüm şuna benzer:

Örnek 2. Bir ifadenin değerini bulun

Örnek 3. Bir ifadenin değerini bulun

Bu negatif rasyonel sayıların çarpımıdır. Negatif rasyonel sayıları çarpmak için modüllerini çarpmanız ve ortaya çıkan cevabın önüne bir artı koymanız gerekir.

Çözüm bu örnek kısaca yazılabilir:

Örnek 4. Bir ifadenin değerini bulun

Bu örneğin çözümü kısaca şöyle yazılabilir:

Örnek 5. Bir ifadenin değerini bulun

Bu rasyonel sayıların farklı işaretlerle çarpımıdır. Bu sayıların modüllerini çarpalım ve ortaya çıkan cevabın önüne eksi koyalım

Kısa çözüm çok daha basit görünecek:

Örnek 6. Bir ifadenin değerini bulun

Karışık sayıyı şuna dönüştürelim: uygunsuz kesir. Gerisini olduğu gibi yeniden yazalım

Rasyonel sayıların farklı işaretlerle çarpımını elde ettik. Bu sayıların modüllerini çarpalım ve ortaya çıkan cevabın önüne eksi koyalım. İfadeyi karmaşıklaştırmamak için modül içeren giriş atlanabilir

Bu örneğin çözümü kısaca yazılabilir.

Örnek 7. Bir ifadenin değerini bulun

Bu rasyonel sayıların farklı işaretlerle çarpımıdır. Bu sayıların modüllerini çarpalım ve ortaya çıkan cevabın önüne eksi koyalım

İlk başta cevabın uygunsuz bir kesir olduğu ortaya çıktı, ancak içindeki kısmın tamamını vurguladık. dikkat bütün kısım fraksiyon modülünden ayrıldı. Ortaya çıkan karışık sayı, önünde bir eksi işareti bulunan parantez içine alındı. Bu, kuralın gereklerinin yerine getirildiğinden emin olmak için yapılır. Ve kural, alınan cevabın önünde bir eksi olmasını gerektiriyordu.

Bu örneğin çözümü kısaca şöyle yazılabilir:

Örnek 8. Bir ifadenin değerini bulun

Öncelikle elde edilen sayıyı kalan 5 sayısı ile çarpalım ve çarpalım. İfadeyi karıştırmamak için modüllü girişi atlayacağız.

Cevap: ifade değeri −2'ye eşittir.

Örnek 9.İfadenin anlamını bulun:

Haydi tercüme edelim karışık sayılar yanlış kesirlere:

Negatif rasyonel sayıların çarpımını elde ettik. Bu sayıların modüllerini çarpalım ve ortaya çıkan cevabın önüne bir artı koyalım. İfadeyi karmaşıklaştırmamak için modül içeren giriş atlanabilir

Örnek 10. Bir ifadenin değerini bulun

İfade birkaç faktörden oluşur. Birleşmeli çarpma yasasına göre, eğer bir ifade birkaç faktörden oluşuyorsa, o zaman ürün eylemlerin sırasına bağlı olmayacaktır. Bu hesaplama yapmamızı sağlar bu ifade herhangi bir sırayla.

Tekerleği yeniden icat etmeyelim, bu ifadeyi faktörler sırasına göre soldan sağa doğru hesaplayalım. İfadeyi karıştırmamak için modül girişini atlayalım

Üçüncü eylem:

Dördüncü eylem:

Cevap: ifadenin değeri

Örnek 11. Bir ifadenin değerini bulun

Sıfırla çarpma yasasını hatırlayalım. Bu yasa, faktörlerden en az birinin olması durumunda ürünün sıfıra eşit olduğunu belirtir. sıfıra eşit.

Örneğimizde faktörlerden biri sıfıra eşit olduğundan, zaman kaybetmeden ifadenin değerinin sıfıra eşit olduğu cevabını veriyoruz:

Örnek 12. Bir ifadenin değerini bulun

Faktörlerden en az birinin sıfıra eşit olması durumunda ürün sıfıra eşittir.

Örneğimizde faktörlerden biri sıfıra eşittir, dolayısıyla zaman kaybetmeden ifadenin değerini cevaplıyoruz. sıfıra eşittir:

Örnek 13. Bir ifadenin değerini bulun

Eylem sırasını kullanabilir ve önce parantez içindeki ifadeyi hesaplayabilir ve ortaya çıkan cevabı bir kesirle çarpabilirsiniz.

Ayrıca çarpmanın dağılım yasasını da kullanabilirsiniz - toplamın her terimini bir kesirle çarpın ve elde edilen sonuçları ekleyin. Bu yöntemi kullanacağız.

İşlem sırasına göre eğer bir ifadede toplama ve çarpma varsa önce çarpma işlemi yapılmalıdır. Bu nedenle ortaya çıkan yeni ifadede çarpılması gereken parametreleri parantez içine alalım. Bu şekilde hangi eylemlerin daha önce, hangilerinin daha sonra gerçekleştirileceğini açıkça görebiliriz:

Üçüncü eylem:

Cevap: ifade değeri eşittir

Bu örneğin çözümü çok daha kısa yazılabilir. Şunun gibi görünecek:

Bu örneğin insanın zihninde bile çözülebileceği açıktır. Bu nedenle bir ifadeyi çözmeden önce analiz etme becerisini geliştirmelisiniz. Muhtemelen zihinsel olarak çözülebilir ve çok fazla zaman ve sinir tasarrufu sağlanabilir. Ve testlerde ve sınavlarda bildiğiniz gibi zaman çok değerlidir.

Örnek 14.−4,2 × 3,2 ifadesinin değerini bulun

Bu rasyonel sayıların farklı işaretlerle çarpımıdır. Bu sayıların modüllerini çarpalım ve ortaya çıkan cevabın önüne eksi koyalım

Rasyonel sayıların modüllerinin nasıl çarpıldığına dikkat edin. Bu durumda rasyonel sayıların modüllerini çarpmak gerekiyordu.

Örnek 15.−0,15 × 4 ifadesinin değerini bulun

Bu rasyonel sayıların farklı işaretlerle çarpımıdır. Bu sayıların modüllerini çarpalım ve ortaya çıkan cevabın önüne eksi koyalım

Rasyonel sayıların modüllerinin nasıl çarpıldığına dikkat edin. Bu durumda rasyonel sayıların modüllerini çarpabilmek için bunu yapabilmek gerekiyordu.

Örnek 16.−4,2 × (−7,5) ifadesinin değerini bulun

Bu negatif rasyonel sayıların çarpımıdır. Bu sayıların modüllerini çarpalım ve ortaya çıkan cevabın önüne bir artı koyalım

Rasyonel sayıların bölünmesi

Tam sayıları bölme kuralları rasyonel sayılar için de geçerlidir. Başka bir deyişle rasyonel sayıları bölebilmek için şunları yapabilmeniz gerekir:

Aksi takdirde, sıradan ve ondalık kesirleri bölmek için aynı yöntemler kullanılır. Ortak bir kesri başka bir kesre bölmek için, ilk kesri ikinci kesrin tersiyle çarpmanız gerekir.

Ve bir ondalık kesri başka bir ondalık kesire bölmek için, bölendeki ve bölendeki ondalık noktayı, bölendeki ondalık noktadan sonraki basamak sayısı kadar sağa kaydırmanız, ardından bölme işlemini bir yöntemle yapmanız gerekir. normal sayı.

Örnek 1.İfadenin anlamını bulun:

Bu, rasyonel sayıların farklı işaretlerle bölünmesidir. Böyle bir ifadeyi hesaplamak için ilk kesri ikincinin tersiyle çarpmanız gerekir.

O halde birinci kesri ikincinin tersiyle çarpalım.

Rasyonel sayıların farklı işaretlerle çarpımını elde ettik. Ve bu tür ifadelerin nasıl hesaplanacağını zaten biliyoruz. Bunu yapmak için bu rasyonel sayıların modüllerini çarpmanız ve ortaya çıkan cevabın önüne bir eksi koymanız gerekir.

Bu örneği sonuna kadar tamamlayalım. İfadeyi karmaşıklaştırmamak için modül içeren giriş atlanabilir

Yani ifadenin değeri

Detaylı çözüm aşağıdaki gibidir:

Kısa bir çözüm şöyle görünecektir:

Örnek 2. Bir ifadenin değerini bulun

Bu, rasyonel sayıların farklı işaretlerle bölünmesidir. Bu ifadeyi hesaplamak için ilk kesri ikincinin tersiyle çarpmanız gerekir.

İkinci kesrin tersi kesirdir. İlk kesri bununla çarpalım:

Kısa bir çözüm şöyle görünecektir:

Örnek 3. Bir ifadenin değerini bulun

Negatif rasyonel sayıların bölümüdür. Bu ifadeyi hesaplamak için, ilk kesri ikincinin tersi ile tekrar çarpmanız gerekir.

İkinci kesrin tersi kesirdir. İlk kesri bununla çarpalım:

Negatif rasyonel sayıların çarpımını elde ettik. Nasıl hesaplanır? benzer ifade zaten biliyoruz. Rasyonel sayıların modüllerini çarpmanız ve ortaya çıkan cevabın önüne bir artı koymanız gerekir.

Bu örneği sonuna kadar bitirelim. İfadeyi karmaşıklaştırmamak için modüllerin bulunduğu girişi atlayabilirsiniz:

Örnek 4. Bir ifadenin değerini bulun

Bu ifadeyi hesaplamak için ilk sayı olan -3'ü kesirle çarpmanız gerekir, karşılıklı kesir.

Bir kesrin tersi kesirdir. İlk sayıyı -3 ile çarpın

Örnek 6. Bir ifadenin değerini bulun

Bu ifadeyi hesaplamak için ilk kesri sayıyla çarpmanız gerekir. sayının karşılıklılığı 4.

4 sayısının karşılığı kesirdir. İlk kesri bununla çarpın

Örnek 5. Bir ifadenin değerini bulun

Bu ifadeyi hesaplamak için ilk kesri −3'ün tersiyle çarpmanız gerekir.

-3'ün tersi bir kesirdir. İlk kesri bununla çarpalım:

Örnek 6.−14,4: 1,8 ifadesinin değerini bulun

Bu, rasyonel sayıların farklı işaretlerle bölünmesidir. Bu ifadeyi hesaplamak için, temettü modülünü bölenin modülüne bölmeniz ve ortaya çıkan cevabın önüne bir eksi koymanız gerekir.

Bölen modülünün bölenin modülüne nasıl bölündüğüne dikkat edin. Bu durumda bunu doğru yapabilmek için yapabilmek gerekiyordu.

Ondalık sayılarla uğraşmak istemiyorsanız (ve bu sıklıkla olur), o zaman bunlar, sonra bu karışık sayıları bileşik kesirlere dönüştürün ve sonra bölmeyi kendisi yapın.

Önceki −14.4: 1.8 ifadesini bu şekilde hesaplayalım. Haydi tercüme edelim ondalık sayılar karışık sayılara:

Şimdi elde edilen tam sayılı kesirleri bileşik kesirlere dönüştürelim:

Artık doğrudan bölme işlemi yapabilirsiniz, yani bir kesri bir kesire bölebilirsiniz. Bunu yapmak için, ilk kesri ikincinin ters kesri ile çarpmanız gerekir:

Örnek 7. Bir ifadenin değerini bulun

−2,06 ondalık kesirini uygunsuz bir kesire dönüştürelim ve bu kesri ikinci kesrin tersiyle çarpalım:

Çok öykülü kesirler

Kesirlerin bölünmesinin kesir çizgisi kullanılarak yazıldığı bir ifadeye sıklıkla rastlayabilirsiniz. Örneğin ifade şu şekilde yazılabilir:

ve ifadeleri arasındaki fark nedir? Gerçekten hiçbir fark yok. Bu iki ifade aynı anlamı taşır ve aralarına eşittir işareti konulabilir:

İlk durumda bölme işareti iki nokta üst üstedir ve ifade tek satıra yazılır. İkinci durumda kesirlerin bölünmesi kesir çizgisi kullanılarak yazılır. Sonuç, insanların aramayı kabul ettiği bir kesirdir çok katlı.

Bu tür çok katlı ifadelerle karşılaştığınızda aynı bölme kurallarını uygulamanız gerekir. sıradan kesirler. İlk kesir ikincinin tersi ile çarpılmalıdır.

Bu tür kesirleri bir çözümde kullanmak son derece sakıncalıdır, bu nedenle bölme işareti olarak kesirli çizgi yerine iki nokta üst üste kullanarak bunları anlaşılır bir biçimde yazabilirsiniz.

Örneğin şunu yazalım çok katlı kesir anlaşılır bir şekilde. Bunu yapmak için öncelikle ilk kesrin nerede ve ikincinin nerede olduğunu bulmanız gerekir çünkü bunu doğru yapmak her zaman mümkün değildir. Çok katlı kesirlerde kafa karıştırıcı olabilecek birkaç kesir çizgisi bulunur. Birinci kesri ikinciden ayıran ana kesir çizgisi genellikle diğerlerinden daha uzundur.

Ana kesir çizgisini belirledikten sonra ilk kesrin nerede, ikincinin nerede olduğunu kolayca anlayabilirsiniz:

Örnek 2.

Ana kesir çizgisini buluyoruz (en uzun olanıdır) ve −3 tam sayısının ortak bir kesire bölündüğünü görüyoruz.

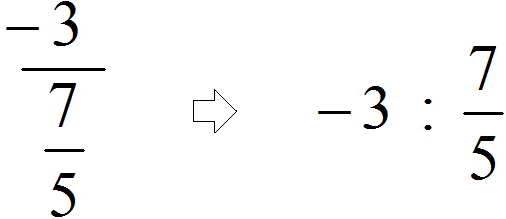
Ve eğer yanlışlıkla ikinci kesir çizgisini ana kesir olarak alırsak (daha kısa olanı), o zaman kesri 5 tam sayısına böldüğümüz ortaya çıkar. Bu durumda, bu ifade doğru hesaplansa bile, Bu durumda bölen −3, bölen ise kesir olduğu için problem yanlış çözülecektir.

Örnek 3.Çok düzeyli kesri açık bir biçimde yazalım

Ana kesir çizgisini buluyoruz (en uzun olanıdır) ve kesrin 2 tam sayısına bölündüğünü görüyoruz

Ve eğer yanlışlıkla ilk kesirli doğruyu baştaki (daha kısa olan) olarak alırsak, o zaman -5 tamsayısını kesire böldüğümüz ortaya çıkar. Bu durumda, bu ifade doğru hesaplansa bile, bu durumda bölen kesir olduğundan ve bölen de 2 tamsayısı olduğundan sorun yanlış çözülecektir.

Çok düzeyli kesirlerle çalışmanın sakıncalı olmasına rağmen, özellikle yüksek matematik çalışırken bunlarla çok sık karşılaşacağız.

Doğal olarak alır ekstra zaman ve yer. Bu nedenle daha fazla kullanabilirsiniz hızlı yöntem. Bu yöntem kullanışlıdır ve çıktı, ilk kesirin zaten ikincinin karşılıklı kesiriyle çarpıldığı hazır bir ifade elde etmenizi sağlar.

Bu yöntem şu şekilde uygulanır:

Örneğin kesir dört katlı ise birinci katta bulunan sayı en üst kata yükseltilir. İkinci katta yer alan figür ise üçüncü kata yükseltilmiştir. Ortaya çıkan sayılar çarpma işaretleriyle (×) bağlanmalıdır

Sonuç olarak, ara gösterimi atlayarak, birinci kesirin zaten ikincinin karşılıklı kesiriyle çarpıldığı yeni bir ifade elde ederiz. Kolaylık ve bu kadar!

Kullanırken hataları önlemek için bu yöntem, aşağıdaki kurala göre yönlendirilebilirsiniz:

Birinciden dördüncüye. İkinciden üçüncüye.

Kuralda hakkında konuşuyoruz katlar hakkında. Birinci kattaki figürün dördüncü kata yükseltilmesi gerekiyor. Ve ikinci kattaki figürün üçüncü kata yükseltilmesi gerekiyor.

Yukarıdaki kuralı kullanarak çok katlı bir kesri hesaplamaya çalışalım.

Böylece birinci katta bulunan sayıyı dördüncü kata, ikinci katta bulunan sayıyı ise üçüncü kata çıkarıyoruz.

Sonuç olarak, ara notasyonu atlayarak, birinci kesirin zaten ikincinin karşılıklı kesiriyle çarpıldığı yeni bir ifade elde ederiz. Daha sonra mevcut bilginizi kullanabilirsiniz:

Yeni bir şema kullanarak çok seviyeli bir kesri hesaplamaya çalışalım.

Sadece birinci, ikinci ve dördüncü katlar var. Üçüncü kat yok. Ancak temel şemadan sapmıyoruz: Figürü birinci kattan dördüncü kata yükseltiyoruz. Üçüncü kat olmadığı için ikinci kattaki numarayı olduğu gibi bırakıyoruz.

Sonuç olarak, ara notasyonu atlayarak, ilk sayı −3'ün zaten ikincinin karşılıklı kesiriyle çarpıldığı yeni bir ifade aldık. Daha sonra mevcut bilginizi kullanabilirsiniz:

Yeni şemayı kullanarak çok katlı kesri hesaplamaya çalışalım.

Sadece ikinci, üçüncü ve dördüncü katlar var. Birinci kat yok. Birinci kat olmadığı için dördüncü kata çıkacak bir şey yok ama ikinci kattan üçüncü kata kadar rakamı yükseltebiliriz:

Sonuç olarak, ara notasyonu atlayarak, ilk kesirin zaten bölenin tersiyle çarpıldığı yeni bir ifade elde ettik. Daha sonra mevcut bilginizi kullanabilirsiniz:

Değişkenleri Kullanma

İfade karmaşıksa ve sorunu çözme sürecinde kafanızı karıştıracak gibi görünüyorsa, ifadenin bir kısmı bir değişkene yerleştirilebilir ve daha sonra bu değişkenle çalışılabilir.

Matematikçiler bunu sıklıkla yaparlar. Zor bir görev bunları daha kolay alt görevlere ayırın ve çözün. Daha sonra çözülen alt görevler tek bir bütün halinde toplanır. Bu yaratıcı süreç ve bu, kişinin yıllar içinde sıkı eğitim yoluyla öğrendiği bir şeydir.

Çok seviyeli kesirlerle çalışırken değişkenlerin kullanımı haklıdır. Örneğin:

Bir ifadenin değerini bulun

Yani payda ve paydada kesirli bir ifade vardır. kesirli ifadeler. Yani yine pek hoşlanmadığımız çok katlı bir kesimle karşı karşıyayız.

Paydaki ifade herhangi bir adla bir değişkene girilebilir, örneğin:

Ama matematikte böyle bir durum Değişkenlere genellikle büyük Latin harfleri kullanılarak adlar verilir. Bu geleneği bozmayalım ve ilk ifadeyi büyük bir harfle belirtelim. Latince harf A

Ve paydadaki ifade büyük harf B ile gösterilebilir

Artık orijinal ifademiz şeklini alıyor. Yani, A ve B değişkenlerine daha önce pay ve paydayı girdikten sonra sayısal ifadeyi bir harfle değiştirdik.

Artık A değişkeninin değerlerini ve B değişkeninin değerini ayrı ayrı hesaplayabiliriz. Bitmiş değerleri ifadeye ekleyeceğiz.

Değişkenin değerini bulalım A

Değişkenin değerini bulalım B

Şimdi ana ifadede A ve B değişkenleri yerine bunların değerlerini koyalım:

“Birinciden dördüncüye, ikinciden üçüncüye” şemasını kullanabileceğimiz, yani birinci kattaki sayıyı dördüncü kata çıkarabileceğimiz, çok katlı bir kesir elde ettik. numara ikinci kattan üçüncü kata kadar bulunur. Daha fazla hesaplama zor olmayacak:

Dolayısıyla ifadenin değeri -1'dir.

Elbette düşündük en basit örnek, ancak amacımız, işleri kendimiz için kolaylaştırmak, hata olasılığını en aza indirmek için değişkenleri nasıl kullanabileceğimizi öğrenmekti.

Bu örneğin çözümünün değişkenler kullanılmadan yazılabileceğini de unutmayın. Şuna benzeyecek:

Bu çözüm daha hızlı ve daha kısadır ve bu durumda bu şekilde yazmak daha mantıklıdır, ancak ifadenin birkaç parametreden, parantezden, köklerden ve kuvvetlerden oluşan karmaşık olduğu ortaya çıkarsa, o zaman bunu hesaplamanız önerilir. ifadelerinin bir kısmını değişkenlere girerek birkaç aşamadan oluşur.

Dersi beğendin mi?
Bize katılın yeni grup VKontakte ve yeni dersler hakkında bildirim almaya başlayın

92 bölüm. II

4) q'yu varsayarsak mutlak değer 1'den küçük, kanıtla

5) Sonsuz bir serinin limiti nedir

1 − 2q + 3q2 – 4q3 + . . . ?

6) İfadelerin Hesaplama Sınırları

(İpucu: 31-33. sayfalarda bulunan sonuçları kullanın.)

4. Rasyonel sayılar ve periyodik ondalık sayılar.

Temsil edilemeyen bu tür rasyonel sayılar p q

sonlu ondalık kesirler biçimindeki sayılar, sıradan "uzun" bölme tekniği kullanılarak sonsuz ondalık kesirlere ayrıştırılır. Bu sürecin her aşamasında sıfıra eşit olmayan bir kalan ortaya çıkar, aksi takdirde kesir sonlu olur. Oluşan çeşitli kalanlar yalnızca 1'den q - 1'e kadar tam sayılar olabilir, dolayısıyla bu kalanların değerleri için yalnızca q - 1 olasılık vardır. Bu, q'luk bir bölmeden sonra kalan k'nın bir kısmının ikinci kez görüneceği anlamına gelir. Ancak daha sonra tüm sonraki kalıntılar, k kalıntısının ilk ortaya çıkışından sonra zaten göründükleri sırayla tekrarlanacaktır. Böylece,

herhangi bir rasyonel sayının ondalık açılımı periyodiklik özelliğine sahiptir; Belirli sayıda ondalık basamaktan sonra aynı grup ondalık basamak tekrarlanmaya başlar sonsuz sayı bir kere. Örneğin, 1 6 = 0,166666666. . .;1 7 = 0,142857142857142857 . . .;

11 1 = 0,09090909. . .;1100 122 = 0,1109090909 . . .;11 90 = 0,122222222 . . . vb. (Temsil edilen rasyonel sayılar hakkında not

son ondalık kesir şeklinde bu son kesir sonuncusundan sonrasını hayal edebiliyoruz ondalık basamak sonsuz tekrarlanan 0 rakamı ve dolayısıyla söz konusu rasyonel sayılar yukarıda verilen genel formülasyonun dışında değildir.) Yukarıdaki örneklerden, rasyonel sayılara karşılık gelen bazı ondalık açılımlar için periyodik bir "kuyruk" olduğu açıktır. öncesinde periyodik olmayan bir "baş" bulunur.

Tersine, her şeyin olduğu gösterilebilir. periyodik kesirler rasyonel sayıları temsil eder. Örneğin sonsuz periyodik kesri düşünün

p = 0,3322222. . .

Şunu yazabilirsiniz: p = 100 33 + 10−3 2(1 + 10−1 + 10−2 + . . .). İfade

§ 2 EŞSİZ BÖLÜMLER. İRRASYONEL SAYILAR, LİMİTLER93

parantez içinde sonsuz var geometrik ilerleme:

İÇİNDE genel durum Kanıt da aynı şekilde oluşturulmuştur ancak biraz hantal bir gösterim ekleme ihtiyacı nedeniyle karmaşık hale gelir. Genel formun periyodik bir kesirini ele alalım

p = 0,a1 a2 a3 . . . ben b1 b2 b3'üm. . . bn b1 b2 b3 . . . bn. . .

B = 0,b1 b2 b3 ile gösterelim. . . genişlememizin periyodik kısmında. O zaman yazabilirsin

p = 0,a1 a2 a3 . . . am + 10−m B(1 + 10−n + 10−2n + 10−3n + . . .).

Parantez içindeki ifade, q = 10−n olan sonsuz bir geometrik ilerlemedir. Formül (10)'a göre bu ilerlemenin toplamı

sonraki nokta 1 − 10 −n'ye eşittir ve bu nedenle

10−m · Bp = 0.a 1 a 2 a 3 . . . a m + 1 − 10 −n .

Egzersizler. 1) Aşağıdaki rasyonel sayıları ondalık kesirlere ayırın: 11 1 .13 1 .13 2 .13 3 .17 1 .17 2 ve genişleme dönemlerini belirleyin.

2) 142.857 sayısı, 2, 3, 4, 5 veya 6 ile çarpıldığında yalnızca rakam permütasyonlarının gerçekleştirilmesi özelliğine sahiptir. Bu özelliği 1 7 sayısının ondalık kesirlere ayrıştırılmasına dayanarak açıklayın.

3) Alıştırma 1'de verilen sayıları çarpanlara ayırın sonsuz kesirler 5, 7 ve 12 numaralı tabanlarla.

4) 1 3 sayısını ikili kesir olarak çarpanlarına ayırın.

5) 0.11212121 açılımını yazın. . . 3 veya 5 tabanında hangi sayıyı temsil ettiğini belirleyin.

5. Büzülebilen bölümler kullanılarak irrasyonel sayıların genel tanımı. 82. sayfada bir ön tanım verdik: “sayı” sonlu veya sonsuz bir ondalık kesirdir. Aynı zamanda, rasyonel bir sayıyı temsil etmeyen ondalık kesirlere irrasyonel sayılar adını vermeyi kabul ettik. Önceki paragrafta elde edilen sonuçlara dayanarak şimdi aşağıdaki formülasyonu önerebiliriz: “sayısal bir süreklilik veya sistem gerçek sayılar("gerçek" sayılar burada "hayali" veya "karmaşık" sayılarla karşılaştırılmaktadır, bkz. § 5), olası tüm sonsuz ondalık kesirlerin bir koleksiyonudur." (Sıfırların atanması,

daha önce de belirtildiği gibi son ondalık kesri yazabilirsiniz

V sonsuz form veya başka bir yol var mı: son rakam a kesirini a - 1 ile değiştirin ve ona sonsuz sayıda dokuz ekleyin. Yani örneğin 0,999'u gördük. . . = 1, - bkz. madde 3.)

Rasyonel sayılar periyodik kesirlerdir; irrasyonel sayılar periyodik olmayan kesirler. Ancak bu tanım bile bütünüyle tatmin edici görünmüyor: Gerçekten de, Birinci Bölüm'de, şeylerin doğası gereği, ondalık sistem diğer olası olanlardan öne çıkan özel bir şey yok; aynı şekilde, örneğin ikili bir sistemle çalışılabilir. Bu nedenle, 10 tabanının veya herhangi bir başkasının özel seçiminden bağımsız olarak sayı sürekliliğinin daha genel bir tanımını vermek son derece arzu edilir. Büyük ihtimalle, en basit yöntem böyle bir genellemeyi ortaya koymak

bir sonrakinde.

Hadi bakalım sayı ekseni bazı diziler I1, I2, I3, . . . , İçinde , . . . rasyonel amaçlara sahip bölümler; Her bir sonraki parçanın bir önceki parçanın içinde yer aldığını ve n'inci parça In'nin uzunluğunun, n süresiz olarak arttıkça sıfıra doğru yöneldiğini varsayalım. Birbiri içine "yuvalanmış" bu tür bir bölümler dizisine, büzülen bölümler dizisi adını vereceğiz. Ondalık kısımlar durumunda, In uzunluğu 10−n'ye eşittir, ancak örneğin 2−n'ye de eşit olabilir veya kendinizi en azından

n 1'den küçük olması şartıyla. Şimdi şunları verelim

Ana geometrik varsayım olarak ele alacağımız formülasyon: Büzülen parçaların sırası ne olursa olsun, sayı ekseninde tüm parçaların aynı anda içerdiği tek ve tek bir nokta vardır. (Doğruların uzunlukları sıfıra yakın olduğundan ve uzunluğu noktalar arasındaki uzaklıktan küçük olan bir doğru parçasına iki farklı nokta sığamayacağından böyle bir noktanın en fazla olduğu açıktır.) Bu nokta, tanımı gereği ve gerçek sayı olarak adlandırılır; rasyonel değilse irrasyonel sayı denir. Bu tanımla noktalar ve sayılar arasında tam bir yazışma kurmuş oluyoruz. Buraya temelde yeni bir şey eklenmemiştir: yalnızca bir sayının sonsuz ondalık kesir olarak tanımına daha genel bir biçim verilmiştir.

Yine de okuyucu bu noktada bazı şüphelere kapılabilir ve bunların tamamen haklı olduğunun kabul edilmesi gerekir. Sayı eksenindeki, varsaydığımız gibi, rasyonel bir sayıya karşılık gelmiyorsa, dizinin tüm daralan bölümlerinde aynı anda bulunan bu "nokta" gerçekte nedir? Cevabımız: sayı doğrusunda varoluş

§ 2 EŞSİZ BÖLÜMLER. İRRASYONEL SAYILAR, LİMİTLER95

Pirinç. 11. Taahhüt bölümleri. Sıra sınırları

Rasyonel uçları olan tüm büzülebilen parçaların içerdiği bir noktanın (geometrik bir görüntüsü olarak kabul edilir) temel geometrik önermedir. Başka matematiksel önermelere yönlendirecek bir indirgemeye gerek yoktur. Bunu, matematikteki diğer aksiyomları veya varsayımları kabul ettiğimiz gibi, sezgisel makullüğüne ve mantıksal olarak yapılandırıldığında ortaya çıkan kullanışlılığına dayanarak kabul ederiz. seri sistem matematiksel cümleler. Tamamen biçimsel olarak, yalnızca rasyonel noktaların toplamı olarak düşüneceğimiz sayı doğrusundan başlayabilir ve sonra irrasyonel noktayı şu şekilde tanımlayabiliriz:

büzülebilen bölümlerin belirli bir dizisini ifade eden bir sembol. İrrasyonel nokta tamamen, uzunlukları sıfıra yaklaşan bir dizi rasyonel parçanın daralmasıyla belirlenir. Bu, temel varsayımımızın aslında bir tanım olarak hizmet edebileceği anlamına gelir. Böyle bir tanımı kabul etmek, irrasyonel bir noktanın "varlığını" doğrulayan sezgisel bir his tarafından büzülen bir dizi parçaya yönlendirildikten sonra, akıl yürütmemizin dayandığı "sezgi koltuk değneklerini" bir kenara atmak ve şunu fark etmek anlamına gelir: her şey matematiksel özelliklerİrrasyonel noktalar, büzülebilen bölümlerin dizilerinin özellikleri olarak anlaşılabilir ve temsil edilebilir.

Saf ile matematiksel nokta Bu durumda önemli olan, irrasyonel sayının tanımını şu şekilde kabul etmiş olmamızdır:

büzülebilen bölümler dizisi, rasyonel sayılar alanındaki ilgili tanımların doğrudan genelleştirilmesi olan ve ayrıca Rasyonel sayılar alanında geçerli olan tüm temel yasalar. Dolayısıyla, örneğin, a ve b sayılarını tanımlayan iki büzülebilen parça dizisine dayalı olarak iki irrasyonel sayı a ve b'nin toplamını belirlemek için şunu oluştururuz: yeni dizi segmentleri daraltmak, başlangıç ​​ve uç noktalar bu dizilere dahil olan bölümler. Aynı şey ab çarpımı, a – b farkı ve a/b bölümü için de yapılabilir. Ve bu tanımlara dayanarak gösterilebilir ki aritmetik yasaları Bu bölümün 1. maddesinde tartışılan irrasyonel sayılara geçilirken ihlal edilmez. Burada ilgili ayrıntıları atlıyoruz.

Tüm bu yasaların doğrulanması basittir ve hiçbir özel zorluk olmadan doğrudan yapılabilir, ancak doğal olarak konuyla ilgilenen acemi bir okuyucu için biraz sıkıcı görünebilir. ne kadar erken o kadar çok Mantıksal temellerini analiz etmektense matematiğin yardımıyla neler yapılabilir? Çoğu zaman bu olur en son ders kitapları matematikçiler okuyucuyu tam da itiyor çünkü daha ilk sayfalardan itibaren gerçek sayılar sistemi için bilgiçlik taslayan bir gerekçe sunuyorlar. Bu sayfaları sakince görmezden gelen okuyucu, şu gerçeğin bilinciyle vicdanını rahatlatsın; XIX sonu yüzyıllar boyunca tüm büyük matematikçiler keşiflerini doğrudan sezgiyle iletilen "saf" sayı sürekliliği kavramına dayanarak yaptılar.

Son olarak, fiziksel nokta Bakış açısına göre, bir irrasyonel sayının büzülebilen bölümler dizisi aracılığıyla tanımlanması doğal olarak tanıma benzetilmektedir. sayısal değer bazı gözlemlenebilir miktarlar - artan doğrulukla ardışık olarak yapılan bir dizi ölçüm yoluyla. Örneğin, belirli bir bölümün uzunluğunu belirlemek amacıyla gerçekleştirilen herhangi bir işlem, yalnızca büyüklüğü cihazın doğruluğu ile belirlenen belirli bir olası hatanın sınırları dahilinde pratik olarak anlamlıdır. Rasyonel sayılar bir doğrunun her yerinde yoğun bir şekilde yer aldığından, ne kadar doğru olursa olsun hiçbir fiziksel işlem, rasyonel sayılar olup olmadığını ayırt etmemize izin vermez. Verilen uzunluk rasyonel veya irrasyonel. Bu nedenle, yeterince tanımlamak için irrasyonel sayılara gerek yok gibi görünüyor. fiziksel olaylar. Ancak Bölüm VI'da göreceğimiz gibi, matematiksel açıklama Fiziksel olaylarda, irrasyonel sayıların kullanılmasıyla elde edilen gerçek avantaj, bu tanımlamanın son derece basitleştirilmesinde yatmaktadır - tam da temeli sayısal süreklilik olan limit kavramının serbestçe kullanılması sayesinde.

§ 2 EŞSİZ BÖLÜMLER. İRRASYONEL SAYILAR, LİMİTLER97

*6. İrrasyonel sayıları belirlemenin diğer yöntemleri. Dedekind bölümleri. İrrasyonel sayıları tanımlamak için biraz farklı bir yol, mantıksal ve mantıksal teorinin en önemli kurucularından biri olan Richard Dedekind (1831-1916) tarafından seçilmiştir. felsefi analiz matematiğin temelleri. Makaleleri - "Stetigkeit und irrationale Zahlen"1 (1872) ve "Was sind und was sollen die Zahlen?"2 (1887) - matematiğin temel ilkelerinin incelenmesi üzerinde derin bir etkiye sahipti. Dedekind, daralan parçaların dizilişi gibi somut yapılara genel soyut kavramları tercih etti. Onun prosedürü "bölüm" fikrine dayanmaktadır; şimdi onun ne olduğunu açıklayacağız.

Diyelim ki, bir şekilde tüm rasyonel sayılar kümesini, B sınıfının her b sayısı, A sınıfının her a sayısından daha büyük olacak şekilde A ve B olmak üzere iki sınıfa bölmenin mümkün olduğunu varsayalım. rasyonel sayılar alanında bir bölüm. Bir kesim yapılırsa, mantıksal olarak akla gelebilecek aşağıdaki üç olasılıktan birinin gerçekleşmesi gerekir.

1) Var en büyük eleman A sınıfında a. Bu durum, örneğin tüm 6 1 rasyonel sayıların A sınıfına atanması ve > 1 olan tüm rasyonel sayıların B sınıfına atanması durumunda ortaya çıkar.

2) B sınıfında en küçük b elemanı vardır. Bu, örneğin tüm rasyonel sayıların A sınıfına atanması durumunda meydana gelir.< 1, к классу B - все рациональные числа > 1.

3) A sınıfında ne en büyük eleman ne de B sınıfında en küçük eleman vardır. Bu tür bir kesit örneğin şu şekilde elde edilecektir:

İle A sınıfı, karesi 2'den küçük olan tüm rasyonel sayıları içerir ve B sınıfı, karesi 2'den büyük olan tüm rasyonel sayıları içerir. Karesi 2 olan hiçbir rasyonel sayının olmadığı gösterildiğinden, A ve B sınıfları tüm rasyonel sayıları kapsar. , mevcut değil.

A sınıfında en büyük a elemanının olduğu ve aynı zamanda B sınıfında da en küçük b elemanının bulunduğu böyle bir durum mantıksal olarak düşünülemez.

ve b, A'nın en büyük elemanından büyük ve B'nin en küçük elemanından küçük olacaktır ve bu nedenle ne A'ya ne de B'ye ait olamaz.

İÇİNDE üçüncü durum, en büyük rasyonel sayının olmadığı durum

V A sınıfı ya da B sınıfının en küçüğü değilse, o zaman Dedekind'e göre bölüm bazı irrasyonel durumları belirler ya da daha doğrusu temsil eder.

1 "Süreklilik ve irrasyonel sayılar". - Yaklaşık. ed.

2 “Sayılar nedir ve ne olmalıdır?” - Yaklaşık. ed.

Geri İleri

Dikkat! Slayt önizlemeleri yalnızca bilgilendirme amaçlıdır ve sunumun tüm özelliklerini temsil etmeyebilir. Eğer ilgileniyorsanız bu iş lütfen tam sürümünü indirin.

Hedefler:

• Rasyonel sayıların tanımını ve sayı kavramının gelişiminin mantıksal şemasını tanıtmak.
• Kavramları anlayın:
• son ondalık kesir;
• sonsuz ondalık kesir;
• periyodik sonsuz ondalık kesir.
• Sıradan bir kesirin türüne göre hangi ondalık kesir (sonlu veya sonsuz) olduğunu belirlemeyi öğrenin.

Görevler:

• Bir eylem algoritması oluşturma ve algoritmaya göre hareket etme yeteneğini geliştirin.
• Elde edilen sonuçları analiz etme, sonuç çıkarma ve yeni sorular sorma yeteneğini geliştirin.
• Sorunları çözerken formüle edilmiş kuralları kullanma yeteneğini geliştirin.
• Diyagramları çizme ve okuma becerilerini geliştirin.

Ders türü: yeni materyal öğrenmek.

Yöntem: problem araştırması.

Biçim: grup

Ders ilerlemesi

Dersin ilk kısmı.

Dersin ilk bölümünün amacı (teorik): Hangi sayıların çağrıldığını ve rasyonel olduğunu ve olmayan sayıların olup olmadığını öğrenin ve anlayın.

1. Dersin başında kısaca tekrarlayın Doğal, kesirli, tam sayı tanımları.

2. Dersin konusu duyurulur: Rasyonel sayılar. Adi ve ondalık kesirler. (Slayt 2). Dersin ilk bölümünün amacı formüle edilmiştir.

4. Doğal olarak şu soru ortaya çıkıyor: Bildiğimiz sayıların hangileri rasyoneldir?? Konuşma sırasında ekranda sayı kavramının gelişiminin mantıksal bir diyagramı çizilir. (Şekil 1 ve Slayt 5).Örnekler verip bildiğimiz sayıların her birinin rasyonel olduğunu kanıtlıyoruz.

Pirinç. 1

5. Ondalık kesirlere daha yakından bakalım. Haydi hatırlayalım ondalık kesri ortak kesire dönüştürme kuralı (Slayt 6) ve yürüt sözlü olarak ondalık kesirleri sıradan kesirlere dönüştürme alıştırması (Slayt 7-12).

(Sözlü olarak)Ondalık kesri ortak kesire dönüştürün: 0,7; 0,75; 0,2; 0,16; 0,125; 0,375.

Kesir ekranda görüntülenir ve çocuklar doğru cevabın bulunduğu kartı alırlar. Önceden bir dizi kart hazırlanır (Ek 1) ve her grubun masasına konur; Kartların üzerinde şu sayılar bulunmaktadır: 7/10, 75/100, 15/20, 3/4, 2/10, 1/5, 8/50, 4/25, 25/200, 1/8, 3/8 , 5/8. Cevaplara yorum yapıyoruz ve gerekirse adım adım kontrol gerçekleştiriyoruz (Slayt 7-12).

6. biz geliyoruz çözüm eğer bir ondalık sayı ortak bir kesirden "türetilmişse" bu ondalık sayı rasyonel bir sayıdır.

Sorun şu şekilde formüle edilmiştir: ondalık kesirlerin neler olabileceği ve tüm ondalık kesirlerin rasyonel sayı olup olmadığı.

7. Sorulan soruları çözmek için gruplar 1 numaralı görevi yerine getirir (Slayt 13–14), (Ek 2).

Görev No. 1.1(grup 1 için)

1/4, 1/3, 1/6 kesirlerini ondalık sayı olarak ifade edin.

Görev No. 1.2(grup 2 için)

2/5, 4/11, 7/15 kesirlerini ondalık sayı olarak ifade edin.

Sonuçlarınızı analiz edin.

Görev No. 1.3(grup 3 için)

3/25, 1/37, 9/44 kesirlerini ondalık sayı olarak ifade edin.

Sonuçlarınızı analiz edin.

Sonuçları analiz ettikten sonra ( Slayt 15) ve gerekiyorsa hesaplamaların kontrol edilmesi (Slayt 16–18), ondalık kesirlerin a) sonlu olduğu sonucuna varıyoruz; b) sonsuz. Ve sonsuz olanların belli bir özelliği vardır: ondalık bir basamaktan başlayarak bir veya daha fazla ondalık basamak tekrarlanır. Bu özellik için, bu tür sonsuz ondalık kesirlere denir periyodik.

Konuşma ilerledikçe tahtaya bir diyagram çizilir. Yazılı işaretler önceden hazırlanır (Ek 3) ve tahtaya mıknatıslarla tutturulur ve oklar tebeşirle çizilebilir.

Pirinç. 2

Çocuklar yapar çözüm sonlu ondalık sayılar ve sonsuz periyodik ondalık sayılar rasyonel sayılardır. Ancak öğretmen, bilginin bu aşamasında bu sonucun yalnızca bir varsayım olduğunu ve yine de şunu kanıtlamanın gerekli olduğunu belirtir. herhangi periyodik bir ondalık kesir ortak bir kesir olarak temsil edilebilir, yani rasyonel bir sayıdır ve bunu daha sonra 9. sınıfta kanıtlayacağız. Şimdilik bu durumu bir gerçek olarak kullanacağız.

8. Daha sonra çocuklardan diyagramı analiz etmeleri ve başka ondalık kesirlerin olup olamayacağını düşünmeleri istenir (ya da onlardan ne sonlu ne de sonsuz periyodik olan bir ondalık kesir bulmaları istenebilir). Hala sonsuz periyodik olmayan kesirlerin olduğu sonucuna varıyoruz. Bu tür kesirlere örnekler veriyoruz (0.01001000100001...; 0.12123123412345123456... vb.) ve bunların rasyonel sayılar olmayacağını söylüyoruz (ve yine bu bizim varsayımımız, bunu kanıtlayabiliriz, ancak daha sonra ancak şimdilik bunu yalnızca bir gerçek olarak kullanacağım).

Pirinç. 3

Dersin ikinci kısmı.

Dersin ikinci bölümünün amacı (pratik): Sıradan bir kesirin görünümünden, bunun sonlu bir ondalık kesir olarak mı temsil edilebileceğini veya sonsuz bir kesir olup olmayacağını nasıl anlayacağınızı öğrenin.

9. Sorunu formüle edelim: Sıradan bir kesirin şekline bakarak bunun sonlu bir ondalık kesir olarak gösterilip gösterilemeyeceğini veya sonsuz bir kesir olup olmayacağını nasıl anlarsınız?

Bu sorunu çözmek için görevleri tamamlayalım. 2-4 numaralı görevlerin her biri gruplar halinde gerçekleştirilir. Her görev tamamlandıktan sonra sonuçlar tartışılır. Her grup kendi sonuçlarını formüle eder.

10. Görev No.2(Slayt 20, Ek 2)

1/20, 1/25, 4/50, 3/125, 5/8, 17/100.

• Bu kesirlerin paydalarını çarpanlarına ayırın.

Sonuçların analiz edilmesi (Slayt 20) (Slayt 21)

11. Görev No.3(Slayt 22, Ek 2)

Kesirleri ondalık sayıya dönüştürün ve soruları cevaplayın.

1/30, 3/110, 7/9, 8/55, 5/111, 7/82.

• Bu kesirlerin paydalarını çarpanlarına ayırın
• Ne ortak mülkiyet bu kesirlerin paydaları var mı?

Sonuçların analiz edilmesi (Slayt 23), gerekiyorsa hesaplamaları kontrol etmek (Slayt 24–27). Her grup gözlemlerini rapor eder ve geçici sonuçlar çıkarır.

12. Görev No.4(Slayt 28, Ek 2)

Önceki üç görevin sonuçlarını analiz edin ve soruları yanıtlayın:

• Sıradan kesirlerden hangi ondalık kesirler türetilir?
• Hangi koşullar altında ortak bir kesir son ondalık sayı olarak gösterilebilir?
• Hangi koşullar altında ortak bir kesir sonsuz periyodik ondalık kesir olarak temsil edilebilir?

4 numaralı görevin sonuçlarına göre her grubun bir temsilcisinin performansını tartıştıktan sonra sonuçlara geçiyoruz.

13. Sonuçlar(Şema 2, Slaytlar 29–31):

1. Ondalık kesirler sonlu veya sonsuz olabilir.
2. Son ondalık sayı her zaman kesir olarak gösterilebilir ve biri rasyonel bir sayıdır.
3. Sonsuz bir periyodik ondalık kesir, ortak bir kesir olarak temsil edilebilir - bu rasyonel bir sayıdır.
4. Herhangi bir sıradan kesir, sonlu veya sonsuz periyodik ondalık kesir olarak temsil edilebilir.
5. Paydanın genişletilmesinde karşılık gelen sıradan ise son ondalık kesir elde edilecektir. indirgenemez kesir başkaları yok asal faktörler 2 ve 5 hariç (Slayt 30).
6. Karşılık gelen sıradan indirgenemez kesrin paydasının açılımında 2 ve 5 dışında başka bir asal faktör mevcutsa sonsuz bir periyodik ondalık kesir elde edilecektir. (Slayt 31).

14. Kuralın uygulanması(Slayt 32–33):

Görev No.5

1. 1/2, 1/3, 7/15, 6/25, 5/16 ortak kesirlerinden hangisi son ondalık kesir olarak gösterilebilir?
2. Hesaplamaları hangi kesirlerde (sıradan veya ondalık) yapmak “daha ​​uygundur”: a) 3/8 + 0,567; b) 2.378 – 3/14 ?
3. Denklemin çözümünü hangi kesirlerde (sıradan veya ondalık) yazacaksınız:
   1. 3x = 8;
   2. 5у = 12;
   3. 16a = –7?

Görevi kontrol ediyoruz ve özetliyoruz:

15. Özetleme ve yeni sorular sorma.(Şekil 4, Slaytlar 34–35). Artık pozitif ve negatif kesirlerin sonlu veya periyodik ondalık kesirler olarak temsil edilebileceğini biliyoruz. Bu, ikincisinin rasyonel sayılar olduğu anlamına gelir. Ancak sonsuz periyodik olmayan ondalık kesirler değildir. Görünüşe göre, henüz sizin bilmediğiniz bazı sayıların alanına giriyorlar (size bunların irrasyonel olarak adlandırıldığına dair bir sır vereceğim). Bu irrasyonel sayılar, rasyonel olanlarla birlikte, özellikleriyle (gerçek sayılar) birleşen kendi sayı alanını da oluştururlar. Ve eğer reel sayılar alanına başka sayılar da “eklerseniz”, o zaman… Ama bu, gelecekteki araştırmanızın konusudur.

Pirinç. 4

16. Dersin sonucu(Slayt 36)

Dersi L.N.'den bir alıntıyla bitiriyoruz. Tolstoy: "Bilgi, ancak hafızayla değil, kişinin kendi düşüncesinin çabasıyla elde edildiğinde bilgidir." Bu doğrultuda her grubun çalışmalarını değerlendiriyoruz.

Ev ödevi:

1. Ders kitabının 37. paragrafını okuyun. Metinde sınıfta tartışmadığımız hangi sorular sunuluyor?
2. Sonlu ondalık kesirlerin “üretildiği” beş sıradan kesir ve sonsuz ondalık kesirlerin “üretildiği” beş sıradan kesir (Ek 4) bulun ve bu kesirleri ondalık sayılara dönüştürün.

Edebiyat:

1. Shvartsburd S.I., Vilenkin N.Ya., Zhokhov V.I., Chesnokov A.S. Matematik 6, Mnemosyne, 2006.
2. Mordkovich A.G. Cebir. 8. sınıf: İleri düzey matematik çalışmaları içeren sınıflar için ders kitabı, Mnemosyne, 2004.