Tanım 1. Sayı ekseni (sayı doğrusu, koordinat doğrusu) Ox, O noktasının seçildiği düz çizgidir orijin (koordinatların orijini)(Şekil 1), yön

Ö → X

Olarak listelenmiş olumlu yön ve uzunluğu kabul edilen bir parça işaretlenir. uzunluk birimi.

Tanım 2. Uzunluğu uzunluk birimi olarak alınan doğru parçasına ölçek denir.

Sayı eksenindeki her noktanın bir koordinatı vardır; gerçek Numara. O noktasının koordinatı sıfırdır. Ox ışını üzerinde bulunan rastgele bir A noktasının koordinatı, OA segmentinin uzunluğuna eşittir. Sayısal eksenin Ox ışını üzerinde yer almayan rastgele bir A noktasının koordinatı negatiftir ve mutlak değerde OA segmentinin uzunluğuna eşittir.

Tanım 3. Düzlemde dikdörtgen Kartezyen koordinat sistemi Oxy ikisini karşılıklı ara dik sayısal eksenler Öküz ve Oy ile aynı ölçek Ve ortak başlangıç geri sayım O noktasında ve Ox ışınından Oy ışınına 90° açıyla dönme yönünde gerçekleştirilecek şekilde saat yönünün tersine(İncir. 2).

Not. Şekil 2'de gösterilen dikdörtgen Kartezyen koordinat sistemi Oxy'ye denir doğru koordinat sistemi, Farklı sol koordinat sistemleri burada Ox ışınının Oy ışınına 90°'lik bir açıyla dönmesi saat yönünde gerçekleştirilir. Bu kılavuzda biz yalnızca sağ elini kullanan koordinat sistemlerini dikkate alıyoruz, özellikle belirtmeden.

Düzlemde bazı dikdörtgen Kartezyen koordinatlar Oxy sistemini tanıtırsak, o zaman düzlemin her noktası elde edilecektir. iki koordinat – apsis Ve koordine etmek aşağıdaki gibi hesaplanır. A düzlem üzerinde keyfi bir nokta olsun. A noktasından dik açıları bırakalım A.A. 1 ve A.A. 2'den sırasıyla Ox ve Oy düz çizgileri (Şek. 3).

Tanım 4. A noktasının apsisi noktanın koordinatıdır A Ox sayı ekseninde 1, A noktasının koordinatı noktanın koordinatıdır A Oy sayı ekseninde 2.

Tanım Noktanın koordinatları (apsis ve koordinat) Dikdörtgen şeklinde bir Kartezyen sistem Oksi koordinatları (Şekil 4) genellikle belirtilir A(X;sen) veya A = (X; sen).

Not. O noktası denir Menşei, koordinatları var Ö(0 ; 0) .

Tanım 5. Dikdörtgen Kartezyen koordinat sisteminde Oxy sayı ekseni Ox'a apsis ekseni adı verilir ve Oy sayısal eksenine ordinat ekseni denir (Şekil 5).

Tanım 6. Her dikdörtgen Kartezyen koordinat sistemi, düzlemi numaralandırması Şekil 5'te gösterilen 4 çeyreğe (çeyreğe) böler.

Tanım 7. Dikdörtgen Kartezyen koordinat sisteminin verildiği düzleme denir. koordinat uçağı.

Not. Apsis ekseni şu şekilde ayarlanmıştır: koordinat uçağı denklem sen= 0, koordinat ekseni koordinat düzleminde denklemle verilir X = 0.

Açıklama 1. İki nokta arasındaki mesafe koordinat uçağı

A 1 (X 1 ;sen 1) Ve A 2 (X 2 ;sen 2)

hesaplanmış formüle göre

Kanıt . Şekil 6'yı düşünün.

Buradan,

Q.E.D.

Koordinat düzleminde bir dairenin denklemi

Oxy koordinat düzleminde (Şekil 7), R yarıçaplı, merkezi bu noktada olan bir daire düşünelim. A 0 (X 0 ;sen 0) .

Düzlemdeki dikdörtgen bir koordinat sistemi, karşılıklı olarak dik iki koordinat ekseni X'X ve Y'Y tarafından oluşturulur. Koordinat eksenleri orijin adı verilen O noktasında kesişir, her eksende pozitif bir yön seçilir. Eksenlerin pozitif yönü (sağ koordinat sisteminde), X'X ekseni döndürüldüğünde seçilir. saat yönünün tersine 90° açıyla pozitif yönü Y'Y ekseninin pozitif yönüyle çakışır. X'X ve Y'Y koordinat eksenlerinin oluşturduğu dört açıya (I, II, III, IV) koordinat açıları denir (bkz. Şekil 1).

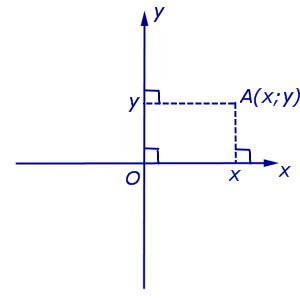
A noktasının düzlem üzerindeki konumu x ve y koordinatları tarafından belirlenir. Seçilen ölçüm birimlerinde x koordinatı OB segmentinin uzunluğuna eşittir, y koordinatı ise OC segmentinin uzunluğuna eşittir. OB ve OC segmentleri A noktasından sırasıyla Y'Y ve X'X eksenlerine paralel çizilen çizgilerle tanımlanır. X koordinatına A noktasının apsisi, y koordinatına da A noktasının ordinatı denir. Şu şekilde yazılır: A(x, y).

A noktası içerideyse koordinat açısı O halde A noktasının pozitif apsisi ve ordinatı vardır. A noktası II koordinat açısında yer alıyorsa, A noktasının negatif apsisi ve pozitif koordinatı vardır. A noktası III koordinat açısında yer alıyorsa, A noktasının negatif apsisi ve ordinatı vardır. A noktası IV koordinat açısında yer alıyorsa, A noktasının pozitif apsisi ve negatif ordinatı vardır.

Uzayda dikdörtgen koordinat sistemi karşılıklı olarak birbirine dik üç koordinat ekseni OX, OY ve OZ tarafından oluşturulur. Koordinat eksenleri orijin adı verilen O noktasında kesişir, her eksende oklarla gösterilen pozitif bir yön ve eksenlerdeki bölümler için bir ölçü birimi seçilir. Ölçü birimleri tüm eksenler için aynıdır. OX - abscissa ekseni, OY - koordinat ekseni, OZ - uygulama ekseni. Eksenlerin pozitif yönü, OX ekseni saat yönünün tersine 90° döndürüldüğünde, eğer bu dönme OZ ekseninin pozitif yönünden gözlemleniyorsa, pozitif yönü OY ekseninin pozitif yönü ile çakışacak şekilde seçilir. Böyle bir koordinat sistemine sağ el denir. Eğer baş parmak sağ el X yönünü X yönü, indeksini Y yönü, ortadakini de Z yönü alırsak sağ koordinat sistemi oluşur. Sol elin benzer parmakları sol koordinat sistemini oluşturur. Karşılık gelen eksenlerin çakışması için sağ ve sol koordinat sistemlerini birleştirmek imkansızdır (bkz. Şekil 2).

A noktasının uzaydaki konumu x, y ve z olmak üzere üç koordinatla belirlenir. X koordinatı OB segmentinin uzunluğuna eşittir, y koordinatı OC segmentinin uzunluğudur, z koordinatı seçilen ölçüm birimlerinde OD segmentinin uzunluğudur. OB, OC ve OD segmentleri A noktasından sırasıyla YOZ, XOZ ve XOY düzlemlerine paralel çizilen düzlemlerle tanımlanır. X koordinatına A noktasının apsisi, y koordinatına A noktasının ordinatı, z koordinatına A noktasının aplikasyonu denir. Şu şekilde yazılır: A(a, b, c).

Orty

Dikdörtgen bir koordinat sistemi (herhangi bir boyutta), koordinat eksenleriyle hizalanmış bir dizi birim vektörle de tanımlanır. Birim vektörlerin sayısı koordinat sisteminin boyutuna eşittir ve hepsi birbirine diktir.

Üç boyutlu durumda, bu tür birim vektörler genellikle şu şekilde gösterilir: Ben J k veya e X e sen e z. Üstelik şu durumda doğru sistem koordinatlar geçerlidir aşağıdaki formüller vektörlerin çapraz çarpımı ile:

• [Ben J]=k ;
• [J k]=Ben ;
• [k Ben]=J .

Hikaye

Dikdörtgen koordinat sistemi ilk kez 1637 yılında Rene Descartes'ın "Yöntem Üzerine Söylem" adlı eserinde ortaya atılmıştır. Bu nedenle dikdörtgen koordinat sistemine aynı zamanda - denir. Kartezyen koordinat sistemi. Geometrik nesneleri tanımlamanın koordinat yöntemi temeli attı analitik geometri. Pierre Fermat da koordinat yönteminin geliştirilmesine katkıda bulundu ancak eserleri ilk olarak ölümünden sonra yayınlandı. Descartes ve Fermat koordinat yöntemini yalnızca düzlemde kullandılar.

için koordinat yöntemi üç boyutlu uzayİlk kez 18. yüzyılda Leonhard Euler tarafından kullanılmıştır.

Ayrıca bakınız

Bağlantılar

Wikimedia Vakfı. 2010.

• Kartezyen koordinat sistemi
• Kartezyen derecesi

Diğer sözlüklerde “Kartezyen koordinatların” ne olduğuna bakın:

KARTEZİN KOORDİNATLARI- (Kartezyen koordinat sistemi) bir düzlemde veya uzayda, genellikle karşılıklı dik eksenlere ve dikdörtgen eksenler boyunca eşit ölçeklere sahip bir koordinat sistemi Kartezyen koordinatları. Adını R. Descartes'tan alıyor... Büyük Ansiklopedik Sözlük

Kartezyen koordinatları- İki dik eksenden oluşan bir koordinat sistemi. Böyle bir sistemdeki bir noktanın konumu, eksenlerin her biri boyunca koordinat merkezinden mesafeyi belirleyen iki sayı kullanılarak oluşturulur. Bilgilendirici konular... ... Teknik Çevirmen Kılavuzu

Kartezyen koordinatları- (Kartezyen koordinat sistemi), bir düzlemde veya uzayda, genellikle karşılıklı dik eksenlere ve eksenler boyunca eşit ölçeklere sahip bir koordinat sistemi; Adını R. Descartes'tan alıyor... ansiklopedik sözlük

Kartezyen koordinatları- Dekarto koordinat durumu T sritis Standartizacija ve metrologija apibrėžtis Tiesinė plokštumos arba erdvės koordinačių sistemi. Joje ašių masteliai paprastai bu lygūs. atitikmenys: İngilizce. Kartezyen koordinatlar vok. Kartesische Koordinatör, f… Metrologijos terminų žodynas'ın kullanımı

Kartezyen koordinatları- Dekarto koordinatės statusas T sritis fizika atitikmenys: engl. Kartezyen koordinatları; ızgara koordinatları vok. kartesische Koordinatör, f rus. Kartezyen koordinatlar, f pranc. Kartvizit koordinatları, f … Fizikos terminų žodynas

KARTEZİN KOORDİNATLARI- bir düzlem üzerindeki noktaların konumunu, iki sabit dik eksene olan mesafelerine göre belirleme yöntemi. Bu kavram, iki bin yıldan fazla bir süre önce Arşimet ve Perga'nın Appologis'inde ve hatta eski Mısırlılar arasında bile görülüyor. İlk defa bu... ... Matematik Ansiklopedisi

KARTEZİN KOORDİNATLARI- Kartezyen koordinat sistemi [adını Fransızlardan almıştır. filozof ve matematikçi R. Descartes (R. Descartes; 1596 1650)], bir düzlemde veya uzayda, genellikle karşılıklı dik eksenlere ve eksenler boyunca eşit ölçeklere sahip dikdörtgen D ... Büyük Ansiklopedik Politeknik Sözlüğü

KARTEZİN KOORDİNATLARI- (Kartezyen koordinat sistemi), bir düzlem üzerinde veya uzayda, genellikle karşılıklı dik eksenlere ve dikdörtgen eksenler boyunca eşit ölçeklere sahip bir koordinat sistemi. Adını R. Descartes'tan alır... Doğal bilim. ansiklopedik sözlük

KARTEZİN KOORDİNATLARI- Kemikler üzerinde bulunan herhangi bir noktanın, dik açıyla kesişen iki eksene göre konumlandırılmasını sağlayan sistem. René Descartes tarafından geliştirilen bu sistem, standart yöntemler grafik gösterimi veri. Yatay çizgi… … Sözlük psikolojide

Koordinatlar- Koordinatlar. Uçakta (solda) ve uzayda (sağda). KOORDİNATLAR (Latince ortak ve ordinatus sıralı kelimesinden gelir), bir noktanın uzayda düz bir çizgi, düzlem, yüzey üzerindeki konumunu belirleyen sayılar. Koordinatlar mesafelerdir... Resimli Ansiklopedik Sözlük

Talimatlar

Yaz matematiksel işlemler metin biçiminde ve bunları adresindeki arama sorgusu alanına girin. ana sayfa Hesap makinesini kullanamıyorsanız ancak İnternet erişiminiz varsa Google sitesi. Bu arama motoru, kullanımı diğerlerinden çok daha kolay olan yerleşik çok işlevli bir hesap makinesine sahiptir. Düğmeli bir arayüz yoktur; tüm veriler tek bir alana metin biçiminde girilmelidir. Örneğin biliniyorsa koordinatlar uç noktalar bölümüç boyutlu koordinat sisteminde A(51,34 17,2 13,02) ve A(-11,82 7,46 33,5), o zaman koordinatlar orta nokta bölüm C((51.34-11.82)/2 (17.2+7.46)/2 (13.02+33.5)/2). Arama sorgusu alanına (51.34-11.82)/2, ardından (17.2+7.46)/2 ve (13.02+33.5)/2 yazarak Google'ı kullanarak aşağıdaki bilgilere ulaşabilirsiniz: koordinatlar C(19,76 12,33 23,26).

Standart denklem daire birkaçını bulmanızı sağlar önemli bilgi bu şekil hakkında, örneğin merkezinin koordinatları, yarıçapın uzunluğu. Bazı problemlerde ise tam tersi verilen parametreler bir denklem oluşturmanız gerekir.

Talimatlar

Size verilen göreve göre çember hakkında hangi bilgilere sahip olduğunuzu belirleyin. Bunu hatırla Nihai amaççapın yanı sıra merkezin koordinatlarını da belirleme ihtiyacıdır. Tüm eylemleriniz bu özel sonuca ulaşmayı amaçlamalıdır.

Koordinat çizgileri veya diğer çizgilerle kesişme noktalarının varlığına ilişkin verileri kullanın. Lütfen daire apsis ekseninden geçerse ikincisinin koordinatı 0, ordinat ekseninden geçerse birincisinin koordinatına sahip olacağını unutmayın. Bu koordinatlar dairenin merkezinin koordinatlarını bulmanızı ve ayrıca yarıçapı hesaplamanızı sağlayacaktır.

Sekantların ve teğetlerin temel özelliklerini unutmayın. Özellikle en kullanışlı teorem, temas noktasında yarıçapın ve teğetin dik bir açı oluşturmasıdır. Ancak kurs sırasında kullanılan tüm teoremleri kanıtlamanızın istenebileceğini lütfen unutmayın.

Bir dairenin denklemi için belirli verilerin nasıl kullanılacağını hemen görmeyi öğrenmek için en standart türleri çözün. Yani, daha önce bahsedilen görevlere ek olarak doğrudan verilen koordinatlar ve kesişme noktalarının varlığı hakkında bilgi verilenler, bir dairenin denklemini derlemek için dairenin merkezi, akorun uzunluğu ve bu akorun bulunduğu bilgiden yararlanabilirsiniz.

Çözmek, inşa etmek ikizkenar üçgen bunun temeli olacak verilen akor, A eşit taraflar– yarıçaplar. Gerekli verileri kolayca bulabileceğiniz derleme. Bunu yapmak için düzlemdeki bir parçanın uzunluğunu bulma formülünü kullanmak yeterlidir.

Konuyla ilgili video

Daire, merkezinden eşit uzaklıkta bulunan bir düzlem üzerinde birçok noktadan oluşan bir şekil olarak anlaşılmaktadır. Merkezden noktalara uzaklık daire yarıçap denir.

Ortak bir kökene (koordinatların kökeni) ve ortak bir uzunluk birimine sahip, birbirine dik, kesişen iki veya üç eksenden oluşan düzenli bir sisteme denir. dikdörtgen Kartezyen koordinat sistemi .

Genel Kartezyen koordinat sistemi (afin koordinat sistemi) mutlaka dik eksenleri içermeyebilir. Şerefine Fransız matematikçi René Descartes (1596-1662), tüm eksenlerde ortak bir uzunluk biriminin ölçüldüğü ve eksenlerin düz olduğu böyle bir koordinat sistemini adlandırdı.

Düzlemde dikdörtgen Kartezyen koordinat sistemi iki ekseni vardır ve uzayda dikdörtgen Kartezyen koordinat sistemi - üç eksen. Bir düzlemdeki veya uzaydaki her nokta, sıralı bir koordinatlar dizisiyle tanımlanır - koordinat sisteminin uzunluk birimine karşılık gelen sayılar.

Tanımdan da anlaşılacağı gibi, düz bir çizgi üzerinde, yani tek boyutta bir Kartezyen koordinat sistemi olduğuna dikkat edin. Bir doğru üzerinde Kartezyen koordinatların kullanılması, bir doğru üzerindeki herhangi bir noktanın iyi tanımlanmış bir gerçek sayıyla, yani bir koordinatla ilişkilendirilmesinin yollarından biridir.

Rene Descartes'ın çalışmalarında ortaya çıkan koordinat yöntemi, tüm matematiğin devrim niteliğinde bir yeniden yapılanmasına işaret ediyordu. Yorumlamak mümkün oldu cebirsel denklemler(veya eşitsizlikler) geometrik görüntüler (grafikler) biçiminde ve tersine bir çözüm arayın geometrik problemler analitik formüller ve denklem sistemlerini kullanma. Evet eşitsizlik z < 3 геометрически означает полупространство, лежащее ниже плоскости, параллельной координатной плоскости xOy ve bu düzlemin 3 birim üzerinde yer almaktadır.

Kartezyen koordinat sistemini kullanarak, belirli bir eğri üzerindeki bir noktanın üyeliği, sayıların aynı olduğu gerçeğine karşılık gelir. X Ve sen bazı denklemleri karşılayın. Böylece, merkezi belirli bir noktada olan bir daire üzerindeki bir noktanın koordinatları ( A; B) denklemi karşılayın (X - A)² + ( sen - B)² = R² .

Düzlemde dikdörtgen Kartezyen koordinat sistemi

Ortak orijinli ve aynı ölçek birim formuna sahip bir düzlem üzerinde birbirine dik iki eksen Düzlemde kartezyen dikdörtgen koordinat sistemi . Bu eksenlerden birine eksen denir Öküz, veya x ekseni , diğeri - eksen Oy, veya y ekseni . Bu eksenlere koordinat eksenleri de denir. ile belirtelim MX Ve Msen sırasıyla, rastgele bir noktanın izdüşümü M eksende Öküz Ve Oy. Projeksiyonlar nasıl alınır? Konuyu geçelim M Öküz. Bu düz çizgi eksenle kesişiyor Öküz noktada MX. Konuyu geçelim M eksene dik olan düz çizgi Oy. Bu düz çizgi eksenle kesişiyor Oy noktada Msen. Bu, aşağıdaki resimde gösterilmektedir.

X Ve sen puan M yönlendirilen segmentlerin değerlerini buna göre arayacağız OMX Ve OMsen. Bu yönlendirilmiş segmentlerin değerleri buna göre hesaplanır. X = X0 - 0 Ve sen = sen0 - 0 . Kartezyen koordinatları X Ve sen puan M apsis Ve koordine etmek . Gerçek şu ki, asıl nokta M koordinatları var X Ve sen, aşağıdaki gibi gösterilir: M(X, sen) .

Koordinat eksenleri düzlemi dörde böler çeyrek daire Numaralandırması aşağıdaki şekilde gösterilmiştir. Ayrıca belirli bir kadrandaki konumlarına bağlı olarak noktaların koordinatlarına ilişkin işaretlerin düzenini de gösterir.

Düzlemdeki Kartezyen dikdörtgen koordinatlara ek olarak kutupsal koordinat sistemi de sıklıkla dikkate alınır. Bir koordinat sisteminden diğerine geçiş yöntemi hakkında - derste kutupsal koordinat sistemi .

Uzayda dikdörtgen Kartezyen koordinat sistemi

Uzaydaki Kartezyen koordinatlar, düzlemdeki Kartezyen koordinatlara tam bir benzetmeyle tanıtılmıştır.

Uzayda birbirine dik üç eksen ( koordinat eksenleri) ortak bir başlangıçla Ö ve aynı ölçek birimiyle oluşturdukları Uzayda Kartezyen dikdörtgen koordinat sistemi .

Bu eksenlerden birine eksen denir Öküz, veya x ekseni , diğeri - eksen Oy, veya y ekseni , üçüncü eksen Oz, veya eksen uygulaması . İzin vermek MX, Msen Mz- keyfi bir noktanın projeksiyonları M eksen üzerindeki boşluk Öküz , Oy Ve Oz sırasıyla.

Konuyu geçelim M ÖküzÖküz noktada MX. Konuyu geçelim M eksene dik düzlem Oy. Bu düzlem eksenle kesişiyor Oy noktada Msen. Konuyu geçelim M eksene dik düzlem Oz. Bu düzlem eksenle kesişiyor Oz noktada Mz.

Kartezyen Dikdörtgen koordinatlar X , sen Ve z puan M yönlendirilen segmentlerin değerlerini buna göre arayacağız OMX, OMsen Ve OMz. Bu yönlendirilmiş segmentlerin değerleri buna göre hesaplanır. X = X0 - 0 , sen = sen0 - 0 Ve z = z0 - 0 .

Kartezyen koordinatları X , sen Ve z puan M buna göre çağrılır apsis , koordine etmek Ve başvurmak .

Çiftler halinde alınan koordinat eksenleri koordinat düzlemlerinde bulunur xOy , yOz Ve zOx .

Kartezyen koordinat sistemindeki noktalarla ilgili problemler

Örnek 1.

A(2; -3) ;

B(3; -1) ;

C(-5; 1) .

Bu noktaların apsis eksenine izdüşümlerinin koordinatlarını bulun.

Çözüm. Bu dersin teorik kısmından da anlaşılacağı gibi, bir noktanın apsis eksenine izdüşümü apsis ekseninin kendisinde, yani eksende bulunur. Öküz ve bu nedenle noktanın kendisinin apsisine eşit bir apsisine ve bir koordinata (eksen üzerindeki koordinat) sahiptir. Oy x ekseninin 0 noktasında kesiştiği nokta), sıfıra eşit. Böylece x eksenindeki bu noktaların aşağıdaki koordinatlarını elde ederiz:

Ax(2;0);

Bx(3;0);

Cx(-5;0).

Örnek 2. Kartezyen koordinat sisteminde noktalar düzlem üzerinde verilir.

A(-3; 2) ;

B(-5; 1) ;

C(3; -2) .

Bu noktaların ordinat eksenine izdüşümlerinin koordinatlarını bulun.

Çözüm. Bu dersin teorik kısmından da anlaşılacağı gibi, bir noktanın ordinat eksenine izdüşümü ordinat ekseninin kendisinde, yani eksende bulunur. Oy ve bu nedenle noktanın kendisinin koordinatına eşit bir koordinata ve bir apsise (eksen üzerindeki koordinat) sahiptir. Öküz Ordinat ekseninin 0 noktasında kesiştiği nokta sıfıra eşittir. Böylece ordinat eksenindeki bu noktaların aşağıdaki koordinatlarını elde ederiz:

Ay(0;2);

By(0;1);

Cy(0;-2).

Örnek 3. Kartezyen koordinat sisteminde noktalar düzlem üzerinde verilir.

A(2; 3) ;

B(-3; 2) ;

C(-1; -1) .

Öküz .

Öküz Öküz Öküz, verilen noktayla aynı apsise ve eşit bir koordinata sahip olacaktır. mutlak değer Belirli bir noktanın koordinatı ve zıt işareti. Böylece eksene göre bu noktalara simetrik olan noktaların aşağıdaki koordinatlarını elde ederiz. Öküz :

A"(2; -3) ;

B"(-3; -2) ;

C"(-1; 1) .

Kartezyen koordinat sistemini kullanarak problemleri kendiniz çözün ve ardından çözümlere bakın.

Örnek 4. Bir noktanın hangi çeyreklerde (çeyrekler, çeyreklerle çizim - “Düzlemde Dikdörtgen Kartezyen koordinat sistemi” paragrafının sonunda) bulunabileceğini belirleyin M(X; sen) , Eğer

1) xy > 0 ;

2) xy < 0 ;

3) X − sen = 0 ;

4) X + sen = 0 ;

5) X + sen > 0 ;

6) X + sen < 0 ;

7) X − sen > 0 ;

8) X − sen < 0 .

Örnek 5. Kartezyen koordinat sisteminde noktalar düzlem üzerinde verilir.

A(-2; 5) ;

B(3; -5) ;

C(A; B) .

Bu noktalara simetrik olan noktaların eksene göre koordinatlarını bulun Oy .

Sorunları birlikte çözmeye devam edelim

Örnek 6. Kartezyen koordinat sisteminde noktalar düzlem üzerinde verilir.

A(-1; 2) ;

B(3; -1) ;

C(-2; -2) .

Bu noktalara simetrik olan noktaların eksene göre koordinatlarını bulun Oy .

Çözüm. Eksen etrafında 180 derece döndürün Oy eksenden yönlü segment Oy bu noktaya kadar. Düzlemin çeyreklerinin gösterildiği şekilde, eksene göre verilen noktaya simetrik olan noktanın olduğunu görüyoruz. Oy, verilen noktayla aynı koordinata sahip olacak ve mutlak değer olarak verilen noktanın apsisine eşit ve işaret olarak zıt bir apsise sahip olacaktır. Böylece eksene göre bu noktalara simetrik olan noktaların aşağıdaki koordinatlarını elde ederiz. Oy :

A"(1; 2) ;

B"(-3; -1) ;

C"(2; -2) .

Örnek 7. Kartezyen koordinat sisteminde noktalar düzlem üzerinde verilir.

A(3; 3) ;

B(2; -4) ;

C(-2; 1) .

Bu noktalara orijine göre simetrik olan noktaların koordinatlarını bulun.

Çözüm. Orijinden verilen noktaya giden yönlendirilmiş parçayı orijin etrafında 180 derece döndürüyoruz. Düzlemin çeyreklerinin belirtildiği şekilde, koordinatların orijinine göre verilen noktaya simetrik bir noktanın, verilen noktanın apsis ve ordinatına mutlak değerde eşit bir apsis ve ordinat sahip olacağını görüyoruz, ancak işareti tam tersi. Böylece orijine göre bu noktalara simetrik olan noktaların aşağıdaki koordinatlarını elde ederiz:

A"(-3; -3) ;

B"(-2; 4) ;

C(2; -1) .

Örnek 8.

A(4; 3; 5) ;

B(-3; 2; 1) ;

C(2; -3; 0) .

Bu noktaların projeksiyonlarının koordinatlarını bulun:

1) uçakta Oksi ;

2) uçakta Öküz ;

3) uçağa Oyz ;

4) apsis ekseninde;

5) ordinat ekseninde;

6) uygulama ekseninde.

1) Bir noktanın düzleme izdüşümü Oksi bu düzlemin üzerinde yer alır ve bu nedenle belirli bir noktanın apsisine ve ordinatına eşit bir apsis ve ordinat ve sıfıra eşit bir aplikasyona sahiptir. Böylece bu noktaların projeksiyonlarının aşağıdaki koordinatlarını elde ederiz. Oksi :

Axy (4; 3; 0);

Bxy (-3; 2; 0);

Cxy(2;-3;0).

2) Bir noktanın düzleme izdüşümü Öküz bu düzlemin kendisinde yer alır ve bu nedenle belirli bir noktanın apsisine ve uygulamasına eşit bir apsis ve uygulamaya ve sıfıra eşit bir koordinata sahiptir. Böylece bu noktaların projeksiyonlarının aşağıdaki koordinatlarını elde ederiz. Öküz :

Axz (4; 0; 5);

Bxz (-3; 0; 1);

Cxz (2; 0; 0).

3) Bir noktanın düzleme izdüşümü Oyz bu düzlemin kendisinde bulunur ve bu nedenle belirli bir noktanın koordinatına ve uygulamasına eşit bir koordinat ve uygulamaya ve sıfıra eşit bir apsise sahiptir. Böylece bu noktaların projeksiyonlarının aşağıdaki koordinatlarını elde ederiz. Oyz :

Ayz(0; 3; 5);

Byz (0; 2; 1);

Cyz (0; -3; 0).

4) Bu dersin teorik kısmından da anlaşılacağı gibi, bir noktanın apsis eksenine izdüşümü apsis ekseninin kendisinde, yani eksende bulunur. Öküz ve bu nedenle noktanın apsisine eşit bir apsise sahiptir ve projeksiyonun ordinatı ve uygulaması sıfıra eşittir (çünkü ordinat ve uygulama eksenleri apsis ile 0 noktasında kesişir). Bu noktaların apsis eksenine izdüşümlerinin aşağıdaki koordinatlarını elde ederiz:

Ax(4;0;0);

Bx(-3;0;0);

Cx(2;0;0).

5) Bir noktanın ordinat eksenine izdüşümü, ordinat ekseninin kendisinde, yani eksende bulunur. Oy ve bu nedenle noktanın kendisinin ordinatına eşit bir ordinatına sahiptir ve projeksiyonun apsisi ve aplikasyonu sıfıra eşittir (apsis ve aplikasyon eksenleri ordinat eksenini 0 noktasında kestiklerinden). Bu noktaların ordinat eksenine projeksiyonlarının aşağıdaki koordinatlarını elde ederiz:

Ay(0; 3; 0);

By (0; 2; 0);

Cy(0;-3;0).

6) Bir noktanın uygulama eksenine izdüşümü uygulama ekseninin kendisinde, yani eksende bulunur. Oz ve bu nedenle noktanın kendisinin uygulamasına eşit bir uygulamaya sahiptir ve projeksiyonun apsisi ve ordinatı sıfıra eşittir (apsis ve ordinat eksenleri uygulama eksenini 0 noktasında kestiklerinden). Bu noktaların uygulama eksenine izdüşümlerinin aşağıdaki koordinatlarını elde ederiz:

Az(0; 0; 5);

Bz(0; 0; 1);

Cz(0; 0; 0).

Örnek 9. Kartezyen koordinat sisteminde noktalar uzayda verilir

A(2; 3; 1) ;

B(5; -3; 2) ;

C(-3; 2; -1) .

Bu noktalara göre simetrik olan noktaların koordinatlarını bulun:

1) uçak Oksi ;

2) uçaklar Öküz ;

3) uçaklar Oyz ;

4) apsis eksenleri;

5) koordinat eksenleri;

6) eksenleri uygulayın;

7) koordinatların kökeni.

1) Noktayı eksenin diğer tarafına “taşıyın” Oksi Oksi, belirli bir noktanın apsisine ve ordinatına eşit bir apsis ve koordinata sahip olacak ve belirli bir noktanın aplikasyonuna büyüklük olarak eşit, ancak işaret olarak zıt bir uygulamaya sahip olacaktır. Böylece, düzleme göre verilere simetrik olan noktaların aşağıdaki koordinatlarını elde ederiz. Oksi :

A"(2; 3; -1) ;

B"(5; -3; -2) ;

C"(-3; 2; 1) .

2) Noktayı eksenin diğer tarafına “taşıyın” Öküz aynı mesafeye. Koordinat uzayını gösteren şekilde, eksene göre belirli bir noktaya simetrik olan bir noktanın olduğunu görüyoruz. Öküz, belirli bir noktanın apsisine ve uygulamasına eşit bir apsis ve uygulamaya ve belirli bir noktanın koordinatına büyüklük olarak eşit, ancak işaret olarak zıt bir koordinata sahip olacaktır. Böylece, düzleme göre verilere simetrik olan noktaların aşağıdaki koordinatlarını elde ederiz. Öküz :

A"(2; -3; 1) ;

B"(5; 3; 2) ;

C"(-3; -2; -1) .

3) Noktayı eksenin diğer tarafına “taşıyın” Oyz aynı mesafeye. Koordinat uzayını gösteren şekilde, eksene göre belirli bir noktaya simetrik olan bir noktanın olduğunu görüyoruz. Oyz, belirli bir noktanın koordinatına ve aplikasyonuna eşit bir ordinat ve aplikasyona ve belirli bir noktanın apsisine değer olarak eşit, ancak işaret olarak zıt bir apsise sahip olacaktır. Böylece, düzleme göre verilere simetrik olan noktaların aşağıdaki koordinatlarını elde ederiz. Oyz :

A"(-2; 3; 1) ;

B"(-5; -3; 2) ;

C"(3; 2; -1) .

Benzetme yoluyla simetrik noktalar düzlemde ve düzlemlere göre verilere simetrik olan uzaydaki noktalarda, uzaydaki Kartezyen koordinat sisteminin bazı eksenlerine göre simetri olması durumunda, simetrinin verildiği eksen üzerindeki koordinatın, işaretini korur ve diğer iki eksendeki koordinatlar, belirli bir noktanın koordinatlarıyla mutlak anlamda aynı, ancak işaret olarak zıt olacaktır.

4) Apsis işaretini koruyacak, ancak ordinat ve uygulama işaretleri değiştirecektir. Böylece apsis eksenine göre verilere simetrik olan noktaların aşağıdaki koordinatlarını elde ederiz:

A"(2; -3; -1) ;

B"(5; 3; -2) ;

C"(-3; -2; 1) .

5) Ordinat işaretini koruyacak, ancak apsis ve aplikasyon işaret değiştirecektir. Böylece, ordinat eksenine göre verilere simetrik olan noktaların aşağıdaki koordinatlarını elde ederiz:

A"(-2; 3; -1) ;

B"(-5; -3; -2) ;

C"(3; 2; 1) .

6) Başvuru sahibi işaretini koruyacaktır ancak apsis ve koordinat işaretleri değişecektir. Böylece, uygulama eksenine göre verilere simetrik olan noktaların aşağıdaki koordinatlarını elde ederiz:

A"(-2; -3; 1) ;

B"(-5; 3; 2) ;

C"(3; -2; -1) .

7) Düzlem üzerindeki noktalarda simetriye benzetilerek, koordinatların orijinine göre simetri olması durumunda, belirli bir noktaya simetrik olan bir noktanın tüm koordinatları, belirli bir noktanın koordinatlarına mutlak değer olarak eşit olacaktır, ama işaret olarak onların tam tersi. Böylece, orijine göre verilere simetrik olan noktaların aşağıdaki koordinatlarını elde ederiz.

Kutupsal koordinatlar

Numara aranır kutup yarıçapı noktalar veya ilk kutupsal koordinat. Uzaklık negatif olamaz, dolayısıyla herhangi bir noktanın kutup yarıçapı . İlk kutupsal koordinat da gösterilir Yunan harfi(“ro”), ancak Latince versiyonuna alışkınım ve gelecekte onu kullanacağım.

Numara aranır kutup açısı verilen nokta veya ikinci kutup koordinatı. Kutup açısı tipik olarak (sözde) içinde değişir. ana açı değerleri). Bununla birlikte, aralığın kullanılması oldukça kabul edilebilir ve bazı durumlarda sıfırdan "artı sonsuza" kadar tüm açı değerlerinin dikkate alınmasına doğrudan ihtiyaç duyulmaktadır. Bu arada derecelerle çalıştığınız için açının radyan ölçüsüne alışmanızı tavsiye ederim. yüksek Matematik comme il faut değil kabul edilir.

Çift çağrılır kutupsal koordinatlar noktalar Bunları bulmak kolaydır ve belirli değerler. Teğet dar açı dik üçgen - karşı tarafın bitişik tarafa oranıdır: dolayısıyla açının kendisi: . Pisagor teoremine göre hipotenüsün karesi toplamına eşit bacakların kareleri: dolayısıyla kutup yarıçapı:

Böylece, .

Bir penguen iyidir ama sürü daha iyidir:


Negatif yönlü açılar Okuyuculardan bazılarının bu yönelimi henüz bilmemesi ihtimaline karşı, bunu oklarla işaretledim. İstenirse her birine 1 tur (radyal veya 360 derece) "vidalayabilirsiniz" ve bu arada rahatlayabilirsiniz tablo değerleri:

Ancak bu "geleneksel" yönelimli açıların dezavantajı, saat yönünün tersine çok fazla (180 dereceden fazla) "bükülmeleri"dir. Şu soruyu tahmin ediyorum: “neden bir kıtlık var ve neden bir kıtlık var? negatif açılar? Matematikte en kısa ve rasyonel yollar. Fizik açısından bakıldığında, dönüş yönü çoğu zaman temel öneme sahiptir - her birimiz kolu yanlış yöne çekerek kapıyı açmaya çalıştık =)

Kutupsal koordinatlarda nokta oluşturma sırası ve tekniği

Güzel resimler güzel ama yerleşik kutup sistemi koordinatları belirlemek oldukça zahmetli bir iştir. Kutup açıları eşit olan noktalarda herhangi bir zorluk yoktur. , örneğimizde bunlar noktalardır ; 45 derecenin katları olan değerler de pek sorun yaratmaz: . Fakat örneğin bir noktayı doğru ve yetkin bir şekilde nasıl inşa edebiliriz?

Kareli bir kağıt parçasına, bir kaleme ve aşağıdakilere ihtiyacınız olacak Çizim aletleri: cetvel, pusula, iletki. İÇİNDE Son çare olarak, tek bir cetvelle, hatta... o olmadan da idare edebilirsiniz! Okumaya devam edin ve bu ülkenin yenilmez olduğuna dair bir kanıt daha göreceksiniz =)

örnek 1

Kutupsal koordinat sisteminde bir nokta oluşturun.

Her şeyden önce şunu öğrenmeniz gerekir: derece ölçüsü açı Köşe tanıdık değilse veya şüpheleriniz varsa, köşeyi kullanmak her zaman daha iyidir. masa veya radyanları dereceye dönüştürmek için genel bir formül. Yani açımız (veya)'dır.

Kutupsal bir koordinat sistemi çizelim (dersin başlangıcına bakın) ve bir iletki alalım. Yuvarlak bir alete sahip olanlar 240 dereceyi işaretlemede zorluk çekmeyeceklerdir, ancak yüksek olasılık Elinizde cihazın yarım daire biçimli bir versiyonuna sahip olacaksınız. Sorun tam yokluk Yazıcınız ve makasınız varsa iletki el işi ile çözüldü.

İki yol vardır: sayfayı ters çevirin ve 120 derece işaretleyin veya yarım tur "vidalayın" ve inceleyin karşı köşe. Yetişkin yöntemini seçelim ve 60 derecelik bir işaret koyalım:


Ya bir Lilliputian iletki ya da dev bir kafes =) Ancak bir açıyı ölçmek için ölçeğin önemi yoktur.

Bir kalem kullanarak direğin içinden geçen ince bir düz çizgi çizin ve yapılan işaret:


Açıyı çözdük, şimdi sırada kutup yarıçapı var. Bir pusula alın ve çizgi boyuncaçözümünü 3 birime ayarladık, çoğu zaman bu elbette santimetredir:

Şimdi iğneyi dikkatlice direğe yerleştirin ve dönme hareketi Küçük bir serif (kırmızı renk) yapıyoruz. Gerekli nokta inşa edildi:


Cetveli doğrudan oluşturulmuş düz çizgiye uygulayarak ve 3 santimetre ölçerek pusula olmadan yapabilirsiniz. Ancak daha sonra göreceğimiz gibi, kutupsal koordinat sistemindeki inşaatı içeren problemlerde tipik bir durum, iki veya daha fazlasını işaretlemeniz gerektiği zamandır. büyük miktar Aynı kutup yarıçapına sahip noktalar olduğundan metalin sertleştirilmesi daha verimli olur. Özellikle çizimimizde pusulanın ayağını 180 derece döndürerek ikinci bir çentik oluşturmak ve direğe göre simetrik bir nokta oluşturmak kolaydır. Bir sonraki paragraftaki materyal üzerinde çalışmak için bunu kullanalım:

Dikdörtgen ve kutupsal koordinat sistemleri arasındaki ilişki

Açıkça hadi ekleyelim Kutupsal koordinat sistemine “düzenli” bir koordinat ızgarası ekleyin ve çizimde bir nokta çizin:

Kutupsal koordinatlarda çizim yaparken bu bağlantıyı akılda tutmak her zaman faydalıdır. Her ne kadar ister istemez, daha fazla ipucu vermeden kendini gösteriyor.

Bir örnek kullanarak kutupsal ve Kartezyen koordinatlar arasındaki ilişkiyi kuralım belirli nokta. Hadi düşünelim dik üçgen Hipotenüsün kutup yarıçapına eşit olduğu ve bacakların Kartezyen koordinat sistemindeki noktanın “X” ve “Y” koordinatlarına eşit olduğu: .

Akut açının sinüsü, karşı tarafın hipotenüse oranıdır:

Dar bir açının kosinüsü orandır bitişik bacak hipotenüse göre:

Aynı zamanda kapsamlı bir okulun 9. sınıf müfredatındaki sinüs, kosinüs (ve biraz daha erken teğet) tanımlarını tekrarladık.

Lütfen referans kitabınıza bir noktanın Kartezyen koordinatlarını kutupsal koordinatları aracılığıyla ifade eden çalışma formülleri ekleyin - bunlarla birden fazla kez ilgilenmemiz gerekecek ve bir dahaki sefere şimdi =)

Noktanın koordinatlarını bulalım dikdörtgen sistem koordinatlar:

Böylece:

Ortaya çıkan formüller, iletki olmadan da yapabileceğiniz zaman inşaat probleminde başka bir boşluk açar: önce noktanın Kartezyen koordinatlarını buluruz (tabii ki taslakta), sonra zihinsel olarak çizimde doğru yeri buluruz ve işaretle bu nokta. Açık son aşama inşa edilen nokta ve direk boyunca geçen ince bir düz çizgi çizin. Sonuç olarak, iddiaya göre açının iletki ile ölçüldüğü ortaya çıktı.

Çok çaresiz durumdaki öğrencilerin bir ders kitabının, not defterinin veya kitapların pürüzsüz kenarlarını kullanarak cetvel olmadan da yapabilmeleri komiktir. not defteri– sonuçta dizüstü bilgisayar üreticileri metrikleri dikkate aldılar, 1 hücre = 5 milimetre.

Bütün bunlar bana, becerikli pilotların bir Belomor paketi boyunca rota çizdikleri iyi bilinen bir şakayı hatırlattı =) Şaka bir yana, şaka gerçeklikten o kadar da uzak olmasa da, bunu Rusya'daki iç hat uçuşlarından birinde hatırlıyorum. Federasyon, uçaktaki tüm navigasyon cihazları arızalandı ve mürettebat, uçağın yere göre açısını gösteren normal bir bardak su kullanarak uçağı başarılı bir şekilde indirdi. Ve uçak pisti - işte burada, ön camdan görülebiliyor.

Dersin başında alıntılanan Pisagor teoremini kullanarak bunu elde etmek kolaydır. ters formüller: , buradan:

"Phi" açısının kendisi standart olarak arktanjant aracılığıyla ifade edilir - kesinlikle aynı karmaşık sayı argümanı tüm sıkıntılarıyla.

İkinci grup formülleri de referans bagajınıza koymanız tavsiye edilir.

Sonrasında detaylı analiz bireysel puanlı uçuşlar, konunun doğal devamına geçelim:

Kutupsal koordinatlarda bir doğrunun denklemi

Esasen, kutupsal koordinat sistemindeki bir doğrunun denklemi şu şekildedir: Kutup yarıçapının kutup açısından fonksiyonu (argüman). Bu durumda kutup açısı dikkate alınır. radyan cinsinden(!) Ve devamlı olarak'dan 'a kadar değerleri alır (bazen sonsuza kadar veya bir takım problemlerde kolaylık olması açısından dikkate alınmalıdır). İçerilen “phi” açısının her değeri ihtisas fonksiyonu, kutup yarıçapının tek bir değerine karşılık gelir.

Polar işlevi bir tür radarla karşılaştırılabilir - bir direkten çıkan bir ışık huzmesi saat yönünün tersine döndüğünde ve bir çizgiyi "algıladığında" (çizdiğinde).

Kutupsal bir eğrinin standart bir örneği Arşimet spirali. Aşağıdaki resim onu ​​gösteriyor İlk tur– kutup açısını takip eden kutup yarıçapı 0'dan şuna kadar değerler aldığında:

Ayrıca, kutup eksenini noktasında kesen spiral, kutuptan sonsuza kadar uzaklaşarak gevşemeye devam edecektir. Ancak benzer vakalar pratikte oldukça nadirdirler; Daha tipik durum, sonraki tüm devirlerde aralıkta elde edilen "aynı çizgide yürüyoruz".

İlk örnekte kavramla karşılaşıyoruz. tanım alanı kutup fonksiyonu: kutup yarıçapı negatif olmadığı için burada negatif açılar dikkate alınamaz.

! Not : bazı durumlarda kullanılması gelenekseldir genelleştirilmiş kutupsal koordinatlar yarıçapın negatif olabileceği durumlarda, bu yaklaşımı biraz sonra kısaca inceleyeceğiz.

Arşimet spiraline ek olarak başka birçok ünlü eğri var, ancak dedikleri gibi sanata doyamazsınız, bu yüzden gerçek pratik görevlerde sıklıkla bulunan örnekleri seçtim.

İlk olarak, en basit denklemler ve en basit çizgiler:

Formun bir denklemi kutuptan çıkanı belirtir ışın. Gerçekten de açı değeri ise bir düşünün Her zaman(“er” ne olursa olsun) sürekli olarak, o zaman hangi satır?

Not : genelleştirilmiş kutupsal koordinat sisteminde verilen denklem direğin içinden geçen düz bir çizgiyi tanımlar

Formun bir denklemi şunu belirler: ilk seferde tahmin edin - eğer herkes için Açı "phi" yarıçapı sabit mi kalıyor? Aslında tanımı bu daire yarıçapın kutbunda ortalanmıştır.

Örneğin, . Açıklık sağlamak için, bu doğrunun denklemini dikdörtgen koordinat sisteminde bulalım. Önceki paragrafta elde edilen formülü kullanarak değiştirmeyi yapıyoruz:

Her iki tarafın karesini alalım:

– bir dairenin denklemi merkez yarıçap 2'nin başlangıç ​​noktasındadır ve kontrol edilmesi gereken de budur.

Makalenin oluşturulmasından ve yayınlanmasından bu yana vektörlerin doğrusal bağımlılığı ve doğrusal bağımsızlığı hakkında Site ziyaretçilerinden şu ruhla bir soru soran birkaç mektup aldım: "Basit ve kullanışlı bir dikdörtgen koordinat sistemi var, neden başka bir eğik koordinat sistemine ihtiyacımız var?" afin durumu?. Cevap basit: matematik her şeyi ve herkesi kucaklamaya çalışır! Ek olarak, belirli bir durumda kolaylık önemlidir - görebileceğiniz gibi, denklemin aşırı basitliği nedeniyle kutupsal koordinatlarda bir daire ile çalışmak çok daha karlı.

Ve bazen matematiksel model tahmin eder bilimsel keşifler. Yani bir zamanlar Kazan Üniversitesi rektörü N.I. Lobaçevski kesinlikle kanıtlandı, başından sonuna kadar keyfi nokta uçaklar çizilebilir sonsuz sayıda düz çizgi, buna paralel. Sonuç olarak, her şey tarafından iftiraya uğradı bilim dünyası, ama... yalanla bu gerçek kimse yapamadı. Yalnızca iyi bir yüzyıl sonra, gökbilimciler uzaydaki ışığın kavisli yörüngeler boyunca ilerlediğini keşfettiler; Lobaçevski'nin bu keşiften çok önce resmi olarak geliştirdiği Öklid dışı geometrisi burada çalışmaya başladı. Bunun, küçük (astronomik standartlara göre) mesafeler nedeniyle eğriliği bizim için görünmeyen, uzayın kendisinin bir özelliği olduğu varsayılmaktadır.

Daha anlamlı inşaat görevlerini ele alalım:

Örnek 2

Bir çizgi oluşturun

Çözüm: Öncelikle bulalım ihtisas. Kutup yarıçapı negatif olmadığından eşitsizliğin geçerli olması gerekir. Trigonometrik eşitsizliklerin çözümüne ilişkin okul kurallarını hatırlayabilirsiniz, ancak basit vakalar bunun gibi, daha hızlı öneririm ve görsel yöntemçözümler:

Bir kosinüs grafiği hayal edin. Henüz hafızanıza kayıtlı değilse sayfada bulun Temel fonksiyonların grafikleri. Eşitsizlik bize ne anlatıyor? Bize kosinüs grafiğinin yerleştirilmesi gerektiğini söyler. Az değil apsis ekseni. Ve bu segmentte oluyor. Ve buna göre aralık uygun değil.

Dolayısıyla fonksiyonumuzun tanım alanı şu şekildedir: yani grafik kutbun sağında bulunur (Kartezyen sistemin terminolojisinde - sağ yarı düzlemde).

Kutupsal koordinatlarda genellikle hangi doğrunun belirli bir denklemi tanımladığı konusunda belirsiz bir fikir vardır, bu nedenle onu oluşturmak için ona ait noktaları bulmanız gerekir; ne kadar çoksa o kadar iyidir. Genellikle bir veya iki düzine (hatta daha az) ile sınırlıdırlar. Elbette en kolay yol, almaktır. masa açısı değerleri. Daha fazla netlik için, negatif değerler Bir tur "vida edeceğim":

Kosinüs paritesi nedeniyle ilgili pozitif değerler tekrar saymanıza gerek yok:

Kutupsal bir koordinat sistemi çizelim ve bulunan noktaları çizelim. aynı değerler Yukarıda tartışılan teknolojiyi kullanarak bir pusula ile eşleştirilmiş çentikler oluşturarak "er" harfini birer birer ertelemek uygundur:

Prensipte çizgi net bir şekilde çizilmiştir, ancak tahmini tamamen doğrulamak için denklemini Kartezyen koordinat sisteminde bulalım. Son zamanlarda türetilen formülleri uygulayabilirsiniz. ama ben sana daha kurnaz bir numaradan bahsedeceğim. Denklemin her iki tarafını da yapay olarak “er” ile çarpıyoruz: ve daha kompakt geçiş formülleri kullanıyoruz:

Vurgulama mükemmel kare, doğrunun denklemini tanınabilir bir forma getiriyoruz:

– bir dairenin denklemi merkezli, yarıçapı 2 olan nokta.

Koşullara göre inşaatı gerçekleştirmek basitçe gerekli olduğundan ve işte bu kadar, bulunan noktaları bir çizgiyle sorunsuz bir şekilde birleştiriyoruz:

Hazır. Biraz düzensiz çıkması sorun değil, bunun bir daire olduğunu bilmenize gerek yoktu ;-)

Aralığın dışındaki açı değerlerini neden dikkate almadık? Cevap basit: hiçbir anlamı yok. Fonksiyonun periyodikliği nedeniyle oluşturulan daire boyunca sonsuz bir koşuyla karşı karşıyayız.

Basit bir analiz yaparak, formdaki bir denklemin, merkezi bir noktada bulunan çapı bir daireyi belirttiği sonucuna varmak kolaydır. Mecazi anlamda konuşursak, bu tür dairelerin tümü kutup ekseni üzerinde "oturur" ve mutlaka kutuptan geçer. Eğer o zaman komik şirket sola - kutup ekseninin devamına doğru göç edecek (nedenini düşünün).

Benzer görev bağımsız karar:

Örnek 3

Bir doğru çizin ve denklemini dikdörtgen koordinat sisteminde bulun.

Sorunu çözme prosedürünü sistematize edelim:

Öncelikle fonksiyonun tanım alanını buluyoruz; bunun için bakmak uygun olur; sinüzoid sinüsün nerede negatif olmadığını hemen anlamak için.

İkinci adımda noktaların kutupsal koordinatlarını kullanarak hesaplıyoruz. masa açısı değerleri; Hesaplama sayısını azaltmanın mümkün olup olmadığını analiz edin?

Üçüncü adımda kutupsal koordinat sistemindeki noktaları işaretliyoruz ve bunları dikkatlice bir çizgiyle birleştiriyoruz.

Ve son olarak doğrunun Kartezyen koordinat sistemindeki denklemini buluyoruz.

Yaklaşık örnekÇözümler dersin sonunda.

Genel algoritma ve inşaat tekniğini kutupsal koordinatlarda detaylandırıyoruz
ve önemli ölçüde hızlandırın dersin ikinci bölümünde, ancak ondan önce başka bir ortak çizgiyle tanışacağız:

Kutup Gülü

Doğru, yaprakları olan bir çiçekten bahsediyoruz:

Örnek 4

Kutupsal koordinatlarda denklemlerle verilen çizgileri oluşturun

Kutup gülü oluşturmanın iki yaklaşımı vardır. Öncelikle kutup yarıçapının negatif olamayacağını varsayarak tırtıklı yolu takip edelim:

Çözüm:

a) Fonksiyonun tanım tanım kümesini bulalım:

Bu trigonometrik eşitsizlik Grafiksel olarak çözmek de zor değil: makalenin materyallerinden Grafiklerin geometrik dönüşümleri Bir fonksiyonun argümanı iki katına çıkarsa grafiğinin ordinat eksenine 2 kat küçüleceği bilinmektedir. Lütfen ilk örnekteki fonksiyonun grafiğini bulun. belirtilen ders. Bu sinüzoid x ekseninin üzerinde nerede bulunur? Aralıklarla . Sonuç olarak, eşitsizlik karşılık gelen bölümler tarafından karşılanır ve ihtisas bizim fonksiyonumuz: .

Genel olarak konuşursak, söz konusu eşitsizliklerin çözümü birliktir. sonsuz sayı bölümler, ancak yine yalnızca bir dönemle ilgileniyoruz.

Belki bazı okuyucular bunu daha kolay bulacaktır analitik metod Tanımın alanını bulduğumda buna şartlı olarak "yuvarlak bir pastayı dilimlemek" diyeceğim. keseceğiz eşit parçalara ve her şeyden önce ilk parçanın sınırlarını bulun. Biz şu şekilde mantık yürütüyoruz: sinüs negatif değildir, Ne zaman onun argümanı 0 ile rad arasında değişir. dahil. Örneğimizde: . Çifte eşitsizliğin tüm kısımlarını 2'ye bölerek gerekli aralığı elde ederiz:

Şimdi saat yönünün tersine sırayla "90 derecelik eşit parçalar kesmeye" başlıyoruz:

– bulunan bölüm elbette tanım alanına dahil edilmiştir;

– sonraki aralık – dahil değildir;

– sonraki bölüm – dahil;

– ve son olarak aralık – dahil değildir.

Tıpkı papatya gibi – “seviyor, sevmiyor, seviyor, sevmiyor” =) Şu farkla ki burada fal falan yok. Evet, bu sadece Çin usulü bir tür aşk….

Bu yüzden, ve çizgi iki özdeş yapraklı bir gülü temsil ediyor. Çizimi şematik olarak çizmek oldukça mümkündür, ancak doğru şekilde bulup işaretlemeniz şiddetle tavsiye edilir. Yaprakların üst kısımları. Köşeler karşılık gelir tanım alanının bölümlerinin orta noktaları, hangisinde bu örnekte bariz açısal koordinatlara sahip . burada taç yaprağı uzunluklarışunlardır:

İşte şefkatli bir bahçıvanın doğal sonucu:

Sinüs sınırlı olduğundan, taç yaprağı uzunluğunun denklemden kolayca görülebileceğine dikkat edilmelidir: , o zaman maksimum değer“Ere” kesinlikle ikiyi geçmeyecek.

b) Bir çizgi oluşturalım, denklem tarafından verilen. Açıkçası, bu gülün taç yaprağının uzunluğu da ikidir, ancak her şeyden önce tanım alanıyla ilgileniyoruz. Uygulanabilir analitik metod"keser": argümanı sinüs negatif değildir sıfırdan “pi”ye kadar olan aralıktadır, bu durumda: . Eşitsizliğin tüm kısımlarını 3'e böleriz ve ilk aralığı elde ederiz:

Daha sonra, "pastayı parçalara ayırmaya" rad ile başlıyoruz. (60 derece):
– segment tanım alanına girecektir;
– aralık – dahil edilmeyecektir;
– segment – ​​sığacak;
– aralık – dahil edilmeyecektir;
– segment – ​​sığacak;
– aralık – dahil edilmeyecektir.

İşlem 360 derecede başarıyla tamamlanır.

Dolayısıyla tanımın kapsamı şu şekildedir: .

Tamamen veya kısmen gerçekleştirilen eylemlerin zihinsel olarak gerçekleştirilmesi kolaydır.

Yapı. Önceki paragrafta her şey dik açılarla ve 45 derecelik açılarla iyi sonuç verdiyse, o zaman burada biraz düzeltmeniz gerekecek. Bulalım Yaprakların üst kısımları. Uzunlukları görevin en başından beri görülüyordu; geriye kalan tek şey, tanım alanının bölümlerinin orta noktalarına eşit olan açısal koordinatları hesaplamaktır:

Yaprakların üst kısımları arasında eşit boşluk olması gerektiğini lütfen unutmayın, bu durumda 120 derecedir.

Çizimin 60 derecelik sektörlere (sınırlandırılmış) işaretlenmesi tavsiye edilir. yeşil çizgiler) ve yaprakların köşelerinin yönlerini (gri çizgiler) çizin. Köşeleri bir pusula kullanarak işaretlemek uygundur - 2 birimlik mesafeyi bir kez ölçün ve 30, 150 ve 270 derecelik çizilen yönlerde üç çentik açın:

Hazır. Bunun zahmetli bir iş olduğunu anlıyorum ama her şeyi akıllıca düzenlemek istiyorsanız zaman harcamanız gerekecek.

Hadi formüle edelim Genel formül : formun bir denklemi, bir doğal sayıdır), taç yaprağı uzunluğu eşit olan kutupsal yapraklı bir gülü tanımlar.

Örneğin, denklem, taç yaprağı uzunluğu 5 birim olan dört yapraklı bir gülü belirtirken, denklem, taç yaprağı uzunluğu 3 birim olan 5 yapraklı bir gülü belirtir. vesaire.